Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная система ALPHA для решения математических проблем управления в условиях неопределенности
Аннотация:
Abstract:
| Авторы: Григоренко Н.Л. (zhalex@yandex.com) - (Московский государственный университет им. М.В. Ломоносова, г. Москва, доктор физико-математических наук | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 11700 |
Версия для печати |
В статье приводится описание программной системы АЛЬФА 2.41, предназначенной для решения задач управления для динамических процессов (в форме обыкновенных дифференциальных уравнений) с управляемыми и неопределенными параметрами. При использовании математических моделей динамических управляемых процессов для проведения прикладных расчетов в экономике, медицине, механике часто встречающиеся вычисления включают решение задач идентификации, анализ свойств математической модели на основе решения задач Коши и краевых задач для систем дифференциальных уравнений, решение задач управления, анализ условий разрешимости задач управления для математической модели при наличии неопределенности, построение управлений, гарантирующих заданное качество процесса при произвольной помехе и вычисление качественных характеристик получающихся решений. Полезной также является библиотека классических математических моделей динамических управляемых процессов с возможностью расчета задач управления для параметров, интересующих пользователя. Система АЛЬФА 2.41 содержит подсистемы для решения обратных задач управления, задачи Коши для систем обыкновенных дифференциальных уравнений, краевые задачи для систем обыкновенных дифференциальных уравнений, библиотеку программ для решения задач оптимального управления в конкретных математических моделях, задачи управления в условиях неопределенности для управляемых динамических систем с линейными уравнениями движения. Приведем три типичных примера использования системы. В первом примере рассмотрим математическую модель распределения капиталовложений развивающейся фирмы [1]. По известной информации о динамике капиталов фирмы за определенный период, взятой из некоторой базы данных, используя программу решения обратных задач, можно настроить параметры модели на изучаемый процесс. Например, часто требуется восстанавливать параметры производственной функции и параметры амортизации. Далее, используя программу решения задачи Коши для дифференциальных уравнений, можно вычислить динамику основных экономических показателей в неуправляемом варианте или с управлением, задаваемом пользователем, и сравнить с реальными показателями. Такая процедура часто повторяется при настройке математической модели на реальный процесс. Следующий уровень корректировки модели обычно связан правильной оценкой ограничений на управляемые параметры, что связано с решением задач управляемости и экстремальных задач. Здесь применяется программа решения краевых задач. Следующий этап исследования модели связан с учетом неопределенных параметров, и пользователю предлагается использовать возможности программы исследования динамических игр. С ее помощью можно оценить ограничения на параметры управления и неопределенности, при которых линеаризованная относительно траектории, задаваемой пользователем, задача управления разрешима, синтезировать управление, гарантирующее заданное качество, и провести расчеты показателей процесса при любой допустимой помехе. В качестве второго примера рассмотрим математическую модель динамики сахара и инсулина в крови при сахарном диабете [2]. Математическая модель процесса описывается системой дифференциальных уравнений с управляемыми и неопределенными параметрами. Целью использования программной системы лечащим специалистом является предсказание динамики изменения показателей пациента при предлагаемом способе лечения и расчеты динамики показателей пациента при различных дозах лекарственных воздействий. По известной информации о динамике индивидуальных показателей пациента за некоторый период, взятой из базы данных, используя программу решения обратных задач, можно найти индивидуальные параметры пациента для рассматриваемой модели. Далее, используя программу решения задачи Коши для дифференциальных уравнений, можно вычислить динамику показателей в неуправляемом варианте или с управлением, задаваемым пользователем, и сравнить ее со средними показателями для той же группы тяжести заболевания. Такая процедура часто повторяется при настройке математической модели на реальный процесс. Следующий уровень корректировки модели обычно связан с решением задач управляемости и экстремальных задач для случая отсутствия неопределенных параметров. Здесь применяется программа решения краевых задач. Следующий этап исследования модели связан с учетом неопределенных параметров, и пользователю предлагается использовать возможности программы исследования динамических игр. С ее помощью можно оценить ограничения на параметры управления и неопределенности, при которых линеаризованная относительно траектории, задаваемой пользователем, задача управления разрешима, синтезировать управление, гарантирующее заданное качество, и провести расчеты показателей процесса при любой допустимой помехе. В третьем примере рассмотрим математическую модель динамики полета транспортного самолета на этапе посадки в условиях ветровых возмущений [3]. Целью использования программной системы инженером является нахождение способа управления самолетом на этапе посадки, гарантирующего безопасность полета при любом допустимом ветровом возмущении, и расчеты динамических характеристик полета при различных ветровых возмущениях. По известной информации о траектории полета за определенный период, взятой из некоторой базы данных, используя программу решения обратных задач, можно настроить параметры модели на изучаемый процесс. Например, часто требуется восстанавливать характеристики работы различных устройств по показаниям черного ящика самолета. Далее, используя программу решения задачи Коши для дифференциальных уравнений, можно вычислить динамику основных показателей с управлением, задаваемым пользователем, и сравнить с реальными показателями. Такая процедура часто повторяется при настройке математической модели на реальный процесс. Следующий уровень корректировки модели обычно связан с выбором ограничений на управляющие параметры, что требует решения задач управляемости и экстремальных задач для случая отсутствия неопределенных параметров. Здесь применяется программа решения краевых задач. Следующий этап исследования модели связан с учетом неопределенных (заранее неизвестных) ветровых возмущений, и пользователю предлагается использовать возможности программы исследования динамических игр. С ее помощью можно оценить ограничения на параметры управления и неопределенности, при которых линеаризованная относительно глиссады задача управления разрешима, синтезировать управление, гарантирующее заданное качество, и провести расчеты показателей процесса при любой допустимой помехе. Программные системы для исследования и расчетов управляемых процессов разрабатываются на кафедре оптимального управления факультета вычислительной математики и кибернетики МГУ и опираются на результаты фундаментальных и прикладных исследований сотрудников кафедры. Описываемая программная система продолжает серию из 11 программных систем для анализа задач управления, описанных в [4, 5]. В разработанных пакетах представлены оригинальные алгоритмы решения задач оптимального управления на основе принципа максимума Понтрягина, новые методы решения неклассических обратных задач управления, краевых задач для обыкновенных дифференциальных уравнений, задач управления в условиях неопределенности в классах контрстратегий и позиционных стратегий. Эти разработки опираются на исследования Л.С. Понтрягина, Н.Н. Красовского, Ю.С. Осипова, Е.Ф. Мищенко, А.В. Кряжимского, М.С. Никольского, В.И. Благо-датских, Н.Л. Григоренко, Ю.Н. Киселева, М.В. Орлова, С.Н. Аввакумова, Д.Б. Силина, Г.Б. Орловой [4-9]. Программная система АЛЬФА 2.41 ориентирована на персональные компьютеры IBM PC, работающие с операционной системой Microsoft Windows-95. Версия системы 2.42 содержит идентичные математические алгоритмы и предоставляет пользователю возможность работать в среде системы АЛЬФА через Internet. Основными принципами, положенными в основу этой серии пакетов, являются: · создание интегрированной среды, ориентированной на решение часто встречающихся задач при исследовании управляемых процессов и автоматизированной системы для их использования, при этом входная и выходная информация алгоритмов унифицирована; · автоматизация поиска параметров процесса для его сходимости при минимальных требованиях к подготовке пользователя в области программирования и математических методов решения задач управления; · широкий набор средств для вычисления функционалов, интересующих пользователя, на результатах решения задач управления; · двойное предназначение пакетов – для научных и учебных целей. Общая характеристика программной системы Программная система ALPHA 2.41 предназначена для настройки параметров математической модели динамических управляемых процессов на изучаемый процесс и для решения задач управления динамическими процессами с неопределенными параметрами. Область применения: исследование и прикладные расчеты математических моделей экономики, экологии, финансовой математики, механики в форме обыкновенных дифференциальных уравнений с управляемыми и неопределенными параметрами. Система АЛЬФА 2.41 содержит: ¨алгоритмы для решения: – обратных задач управления, – задачи Коши для систем обыкновенных дифференциальных уравнений, – краевых задач для систем обыкновенных дифференциальных уравнений, – задач управления в условиях неопределенности для управляемых динамических систем с линейными уравнениями движения, ¨ библиотеку программ для решения задач оптимального управления в конкретных математических моделях. Программная система АЛЬФА 2.41: * предназначена для расчетов и визуализации решений в математических моделях динамических управляемых процессов с неопределенными параметрами, описываемых обыкновенными дифференциальными уравнениями; * позволяет вводить исследуемую задачу на естественном математическом языке, получать результаты расчетов соответствующих задач в графической и цифровой форме; * является инструментом в применении современной теории динамических игр. Программные подсистемы, входящие в систему АЛЬФА 2.41 Подсистема для исследования обратных задач управления. Постановка задачи. Рассматривается система дифференциальных уравнений с управляемыми параметрами
где u(t) – вектор управления, принадлежащий выпуклому компакту U. Требуется по известной информации о фазовом векторе x(t), 0 Подходы к решению обратных задач, реализованные в программе. В программе реализованы устойчивые позиционные алгоритмы динамического восстановления управлений для линейных и нелинейных по управлению систем, сформулированные в [6, 7]. Предусмотрены возможности решения задачи восстановления управлений в случае наличия информации только о части координат фазового вектора системы, широкие возможности автоматического и ручного выбора регуляризирующих параметров. Информация о фазовом векторе системы может обрабатываться из файла либо из базы данных. Предусмотрены вывод численной и графической информации о восстановленном управлении и возможность вычисления различных функционалов на управлении и траектории. Подсистема предназначена для расчетов и визуализации решений обратных задач в математических моделях динамических процессов, описываемых обыкновенными дифференциальными уравнениями; позволяет вводить исследуемую задачу на естественном математическом языке, получать результаты расчетов соответствующих задач в графической и цифровой форме. Подсистема для решения задачи Коши для систем обыкновенных дифференциальных уравнений. Постановка задачи. Для системы дифференциальных уравнений
найти решение, удовлетворяющее начальному условию x(t0)=x0 . Подходы к решению задачи Коши, реализованные в программе. В программе реализованы одношаговые и многошаговые методы решения обыкновенных дифференциальных уравнений, численные методы решения жестких систем: Эйлера, Рунге-Кутта 2-го и 4-го порядков, Рунге-Кутта-Фельдберга, Адамса, Гира, Грэгга-Булирша-Штерна. Общее описание программы. Ввод задачи осуществляется пользователем на естественно-научном языке. Пользователю предоставлены возможности задавать начальные значения системы с помощью клавиатуры и мыши, интегрировать систему в прямом и обратном времени, получать траектории для большого числа начальных значений, рисовать вспомогательные кривые и поверхности на фазовой плоскости системы, сохранять фазовые портреты и отдельные траектории и выводить их на печать. Подсистема для исследования краевых задач для систем обыкновенных дифференциальных уравнений. Постановка задачи. Найти численное решение краевой задачи для системы дифференциальных уравнений: Пусть краевая задача имеет вид:
Здесь Библиотека программ для решения задач оптимального управления в конкретных математических моделях. Библиотека включает в себя программы Вольтерра 1.51, Рамсей 1.61, Пума 1.71. Программа Вольтерра 1.51. Постановка задачи. Рассматривается модель динамики численности двух популяций Лотки-Вольтерра с управляемыми параметрами:
Здесь x – численность популяции жертв в момент t; y – численность популяции хищников в момент t; a, b, c, d, e, f – положительные параметры; u – управляющий параметр, удовлетворяющий ограничению 0 £ u £ umax . Рассматривается задача о нахождении управления, приводящего фазовый вектор из начального положения x0 , y0 в положение равновесия и минимизирующего интегральный показатель качества Подходы к решению задач управления, реализованные в программе. В программе реализована численная процедура решения задачи оптимального управления на основе Принципа максимума Понтрягина. Общее описание программы. Пользователь имеет возможность вводить параметры модели и получать картину синтеза оптимальных траекторий. Для конкретной начальной позиции предусмотрен расчет оптимальной траектории, вычисление времени прихода фазовой точки в положение равновесия и вычисление функционалов, задаваемых пользователем на соответствующих траекториях, и в управлении. Программа Рамсей 1.61. Постановка задачи. Рассматривается модель динамики изменения капитала развивающейся фирмы, описываемая уравнениями:
K(0)= K0 , 0 £ t £ T, K(T) / L ³ kT ³ 0. Здесь K(t) – капитал фирмы в момент t; L – численность работающих в момент t; m – коэффициент амортизации – положительный параметр; s(t) – управляющий параметр, удовлетворяющий ограничению 0£ s(t)£ 1. Рассматривается задача о нахождении управления, переводящего систему из заданного начального состояния в конечное K(T):K(T) / L ³ kT и максимизирующего интегральный показатель качества Пользователь имеет возможность ввести параметры модели и получить картину синтеза оптимальных траекторий. Для конкретной начальной позиции предусмотрены расчеты оптимальной траектории, оптимального управления и вычисление функционалов, задаваемых пользователем на соответствующих траекториях, и в управлении. Программа Пума 1.71. Рассматривается математическая модель робота типа Пума с шестью управляющими параметрами. Требуется найти управление, переводящее схват робота из одной точки фазового пространства в другую и минимизирующее один из функционалов качества – быстродействие или суммарный расход энергии. Программа предназначена для тренировки навыков ручного управления роботами этого типа. Она оценивает результаты ручного управления и показывает наилучшие в том или ином смысле решения. Подсистема для решения задачи управления в условиях неопределенности для управляемых динамических систем с линейными уравнениями движения. Постановка задачи. Рассматривается движение конфликтно управляемого вектора x Î Rn, описываемое системой уравнений:
Здесь u Î P Ì Rp, v Î Q Ì Rq; P, Q – компакты из евклидовых пространств Rp, Rq; A(t), B(t), C(t) – матрицы соответствующих размерностей. Вектор u(t) находится в распоряжении первого игрока, вектор v(t) находится в распоряжении второго игрока. Движение начинается в момент t=t0 из начального состояния x(t0)=x0 и протекает под воздействием функций u(t)ÎP, v(t)ÎQ. В пространстве Rn выделено некоторое непустое замкнутое множество М, которое называется терминальным. Цель первого игрока – добиться по возможности быстрого выполнения включения x(t1)Î M при некотором t1 ³ t0. В момент первого попадания точки x(t) на М игра считается законченной. Второй игрок стремится отдалить момент попадания x(t) на М или, если это возможно, обеспечить при всех t ³ t0 условие x(t)ÏM. Требуется для данных параметров процесса и начального состояния указать, разрешима ли задача управления для первого игрока и вычислить управление первого игрока, гарантирующее окончание игры за конечное время. Подходы к решению игровых задач, реализованные в программе. В программе реализованы алгоритмы первого и второго прямых методов Понтряги- на [2]. Общее описание программы. Ввод задачи предусмотрен на естественно-научном языке. Множества P, Q, M описываются их опорными функциями. Имеется обширная библиотека классических игровых моделей. Программа выдает информацию о разрешимости задачи об окончании игры, вычисляет гарантированное время окончания игры и стратегию первого игрока в одном из классов, определяемых пользователем: контрстратегий (в фиксированный момент времени и к нефиксированному моменту времени) и позиционных стратегий (в фиксированный момент времени и к нефиксированному моменту времени) [2]. После этих расчетов программа готова к реализации управления при любом допустимом управлении второго игрока (помехе). Пользователь имеет возможность ввести помеху в виде функции, заданной аналитически, из некоторой базы данных, а также с клавиатуры, джойстика или мышью. После расчета траектории он может вычислить значения интересующих его функционалов на полученных управлениях и траектории. Список литературы 1. Ашманов С.А. Введение в математическую экономику. - М., Наука. - 1984. 2. Денисова М.Ю. Задача управления в условиях неопределенности для математической модели сахарного диабета. - Вестник МГУ. сер. 15. - Вычислительн. матем. и кибернетика.-№3. - 1994. 3. Кейн В.М., Пацко В.С., Турова В.Л. Задача о посадке самолета в условиях сдвига ветра: Сб. Управление в динамических системах. - Свердловск. - 1990. - с.52-64. 4. Григоренко Н.Л., Киселев Ю.Н., Орлов М.В. Пакеты прикладных программ для решения прямых и обратных задач управления. Компьютерные технологии в высшем образовании. - Изд-во МГУ. - 1994.- С.346-364. 5. Grigorenko N.L., Kiselev Yu. N., Orlov M.V., Ria- bov A. Yu. Differential equations, linear time optimal control and linear Quadratic Control through conputer Experiments. ALPHA: An animator/simulator for controlled dynamical systems for IBM personal computers. Pub. MSU. - 1994. 6. Осипов Ю.С. Кряжимский А.В. Об устойчивом восстановлении управления по измерениям части координат: Сб. Некоторые задачи управления и устойчивости. - Свердловск. - 1989. - С.33-47. 7. Осипов Ю.С., Кряжимский А.В. О моделировании управления в динамической системе // Изв. АН СССР. Техническая кибернетика. - 1983. - С.51-60. 8. Киселев Ю.Н. Схема продолжения по параметру при решении краевых задач для обыкновенных дифференциальных уравнений. - Изд-во МГУ. - 1996. 9. Понтрягин Л.С. Линейные дифференциальные игры преследования: Матем. сб. - 1980. - Т.112. - №3. - Ñ.307-330. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1050 |
Версия для печати |
| Статья опубликована в выпуске журнала № 4 за 1997 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Разработка загрузчика программного обеспечения встроенной системы управления
- Оптимизация обработки информационных запросов в СУБД
- Методика экономической оценки потребительского качества программных средств
- Унифицированный информационный интерфейс и его реализация в комплексной САПР
- Интеграция инструментальных средств создания программного обеспечения
Назад, к списку статей



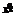 =F(t, x, u), x Î En, u Î Rl, u Î U, 0 £ t £ T,
=F(t, x, u), x Î En, u Î Rl, u Î U, 0 £ t £ T,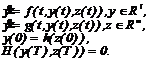
 гладкие векторные функции. Предполагая существование решения краевой задачи, рассмотрим вопрос о его вычислении. Для решения краевой задачи в пакете реализован ряд модификаций метода продолжения по параметру, предложенный в работе [8]. Метод продолжения по параметру можно рассматривать как определенное развитие и модификацию метода Ньютона. Основная идея метода продолжения в непрерывной форме может быть сформулирована предельно просто – сведение краевой задачи к задаче Коши.
гладкие векторные функции. Предполагая существование решения краевой задачи, рассмотрим вопрос о его вычислении. Для решения краевой задачи в пакете реализован ряд модификаций метода продолжения по параметру, предложенный в работе [8]. Метод продолжения по параметру можно рассматривать как определенное развитие и модификацию метода Ньютона. Основная идея метода продолжения в непрерывной форме может быть сформулирована предельно просто – сведение краевой задачи к задаче Коши.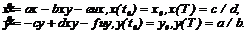
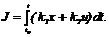
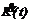 =s(t)F(K(t),L)- mK(y),
=s(t)F(K(t),L)- mK(y),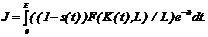
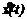 =A(t)x(t)+B(t)u(t)-C(t)v(t), x(t0)=x0.
=A(t)x(t)+B(t)u(t)-C(t)v(t), x(t0)=x0.