...интуиция – деликатное оружие, которым надо уметь пользоваться, и помогает этому самая обыкновенная "выучка". В частности, в математике и физике полученные интуитивно результаты должны быть возможно скорее подтверждены строгими рассуждениями. Самую интуицию надо тренировать в том направлении, чтобы вместе с результатом она могла найти подтверждающее его достаточно простое рассуждение или короткую изящную выкладку.
А.Н. Колмогоров
Развитие современной вычислительной техники достигло новой фазы – фазы создания ЭВМ пятого поколения, одной из главных особенностей которых является их максимальная приближенность к пользователю. Этого можно достичь только благодаря повышению "интеллектуального" уровня ЭВМ, что позволит устранить промежуточное звено путем передачи функции программиста самой ЭВМ.
Чем выше "интеллектуальный" уровень ЭВМ, тем шире ее возможности, а значит и круг ее пользователей. Наделение ЭВМ функциями искусственного интеллекта позволяет ей решать такие сложные задачи, как перевод текста с одного языка на другой, доказательство теорем, игра в соответствии с заданными правилами (шахматы) и др. В практическом плане это ведет к повышению эффективности научных исследований, улучшению качества различного рода управляющих систем, к повышению производительности труда во всех сферах деятельности человека. Именно это является главной причиной интенсивных исследований, проводимых во многих странах мира по проблеме искусственного интеллекта (ИИ) [1;2]. В нашей стране данной проблемой также занимается целая плеяда ученых, усилиями которых, в частности, разработан справочник по ИИ [3], выпущенный в трех книгах. Различным вопросам, связанным с проблемой ИИ, посвящены и публикации [4-8].
Уже в начале 70-х годов произошел качественный скачок в исследованиях по ИИ. Это обусловлено, по крайней мере, двумя факторами: во-первых, стало ясно, что ранее созданным программам "не хватает профессиональных знаний" в соответствующей области; во-вторых, надо "научить" программу самостоятельно собирать необходимую информацию на основе логической обработки результатов опроса экспертов.
Решение этих двух задач становится возможным по мере изучения работы человека и, прежде всего, его мозга, при решении различных проблем. Это направление исследований неотделимо от проблемы ИИ, и ему также посвящена обширная публикация (см. библиографию в [9]. Проблемы работы мозга и научного творчества и ранее интересовали многих крупных ученых: Адамар Ж. [10], Пойа Д. [11], Колмогоров А.Н. [12] и др.). Работа мозга, отличаясь большой гибкостью и интуитивностью мышления, несравнима с работой детерминированной программы ЭВМ. Проблема "интеллектуализации" работы программы ЭВМ путем придания ей большей гибкости и эвристичности "мышления" является важнейшей научной задачей теории эвристических решений [9], теснейшим образом связанной с проблемой ИИ. Только программа, наделенная элементами интеллекта, способна обобщать большие объемы информации, анализировать ее и приводить к виду, удобному для использования лицом, принимающим решение (ЛПР). Накопление "опыта" в ходе обработки информации и анализа ответов, получаемых от экспертов, позволяет ЭВМ, обладающей такой программой, "обучаться" в той или иной специальной области знаний и в дальнейшем выдавать пользователю более качественную и обобщенную информацию. Возможность подобного "обучения" программы, приобретения ею элементов эвристики, отличающих ее от жестких детерминированных программ, и некоторые детали эвристического подхода проиллюстрируем на следующем примере.
Задана матрица технологических коэффи-циентов a= êêaij êê, где aij – расход i-го вида ре-сурсов
( ), требуемый для производства единицы продукции j-го вида (
), требуемый для производства единицы продукции j-го вида (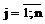 ). ?Прибыль cj, получаемая от реализации единицы продукции j-го вида задана вектор-строкой c=(cj)n. Задан также запас ресурсов каждого вида (вектор-столбец b= êêbi êêm):
). ?Прибыль cj, получаемая от реализации единицы продукции j-го вида задана вектор-строкой c=(cj)n. Задан также запас ресурсов каждого вида (вектор-столбец b= êêbi êêm):
 (1)
(1)
Требуется найти такой план выпуска продукции (вектор X=(xj), где xj – количество продукции j-го вида), который обеспечит при настоящих условиях наибольшую суммарную прибыль. Данная задача формализуется в виде задачи линейного программирования (ЗЛП):
L(X) = 2x1+3x2+5x3 ® max (2)
X
x1 + +2x3 £ 6,
2x1 + x2+ x3 £ 5, "xj ³ 0. (3)
2x2+3x3 £ 5
Целевая функция (2) - это суммарная прибыль, получаемая при варианте выпуска продукции Х, а ограничения (3) отражают тот факт, что расход ресурсов при варианте Х (левые части неравенств) не должен превышать их запасы (правые части неравенств).
Решение ЗЛП (2), (3), полученное известными методами [13,14], приводит к оптимальному плану:
Xo=( 5/3 ; 0 ; 5/3 ), Lmax=L(Xo)=35/3,
при этом одна единица ресурса первого вида остается неиспользованной. Возникает естественный вопрос: какова будет дополнительная прибыль, если по существующим ценам реализовать избытки русурсов и закупить их еще в необходимом количестве? Вопрос может быть поставлен и более радикально: каким образом следует потратить исходный бюджет Q ед. на покупку ресурсов bi m видов, чтобы при этом была обеспечена наибольшая прибыль (с учетом оптимальности производства)?
Оба вопроса приводят к необходимости варьирования параметрами bi (1) исходной задачи ЛП (2), (3), то есть к необходимости решения параметрической ЗЛП. В [15, с.116] указывается на трудности, возникающие при решении парамет-рических ЗЛП, и трудоемкость вычислительных процедур при их решении. Следовательно, даже если в распоряжении ЛПР имеется экспертная система (ЭС), способная отвечать на подобного ряда вопросы, то для решения параметрической ЗЛП при большой размерности (m´ n) задачи, на решение может потребоваться значительное время даже при высокой производительности ЭВМ. Это затруднило бы общение с ЭС в режиме реального времени.
Теперь рассмотрим, насколько просто мог бы получить ответ на каждый из этих вопросов специалист в данной предметной области (то есть экономист), обладающий достаточным опытом, хорошо развитым эвристическим мышлением и интуицией.
Так как расходы ресурсов на 1 ед. продук-
ции и их стоимости si (s=êêsi êêm) известны, то
экономист определяет полные затраты зj на единицу продукции j-го вида :
зj
 (4)
(4)
В частности, для данного числового примера (1), задав вектор стоимостей sT=(2;1;3) и воспользовавшись (4), (1), получим:
з1=2×1+1×2+3×0=4,
з2=2×0+1×1+3×2=7, т.е. з
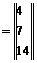 . (5)
. (5)
з33=2×2+1×1+3×3=14
На основании данных (1) (5) экономист определяет удельную эффективность производства каждого вида продукции Rj как прибыль, приходящуюся на единицу полных затрат:
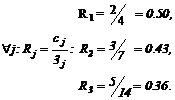 (6)
(6)
В экономике показатель R давно известен и именуется рентабельностью.
Экономист делает вывод, что выпускать следует только продукцию первого вида, так как она обладает наибольшей рентабельностью, а значит, и общая прибыль будет наибольшей. Если показатели сj и зj " j не изменя- ются по мере вы-пуска продукции, то вто- рой вывод, который делает экономист, за-ключается в том, что весь исходный бюджет
Q= si bi =2×6+1×5+3×5=32??.
si bi =2×6+1×5+3×5=32??.
следует направить для закупки ресурсов, требуемых для выпуска только изделий 1-го вида. При этом будет выпущено x10 единиц продукции 1-го вида:
 ??.
??.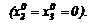
Количество оптимально закупаемого ресурса каждого вида так же находится по элементарной формуле:

Максимальная прибыль, обеспечиваемая при этом как за счет оптимальной стратегии выпуска продукции, так и за счет оптимальной стратегии закупки русурсов, будет равна:
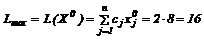 ед.
ед.
Только благодаря оптимальной стратегии закупки прибыль увеличилась с 11.7 до 16.0 единиц (на ~ 37%).
Таким образом, решение сложной математической задачи, благодаря эвристическим приемам, вытекающим из анализа содержательной постановки, позволило существенно упростить решение без потери точности.
По мере усложнения постановок задач решение, получаемое на основе эвристического программирования, как правило, оказывается приближенным. Это, однако, не может являться достаточной причиной отказа от него, если нет других способов решения и, тем более, может быть получена оценка возможной погрешности. Рассмотрим еще один числовой параметр, который позволит проиллюстрировать возможность обобщения эвристического подхода, примененного в предыдущем случае, уже для решения чисто математической задачи [17]:
 (7)
(7)
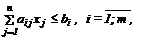 (8)
(8)
xj Îí0;1ý, " j . (9)
где xj - двузначные (булевы) переменные.
Другой целью рассмотрения данной задачи является формулировка эвристического алгоритма, обеспечивающего вполне удовлетворительное решение задачи (7)-(9), охватывающей довольно обширную область практических ситуаций, укладывающихся в ее формальную схему. Рассмотрим конкретный числовой параметр, который прояснит некоторые детали эвристического подхода и позволит наметить основные идеи алгоритма.
Требуется из n=6 предметов различной ценности (вектор-строка С=(сj)) погрузить в самолет некоторое их количество, при котором суммарная ценность (7) будет наибольшей, а общий вес не превысит величину b=60 единиц. Ценности сj и веса предметов aj записаны в таблице 1.
Таблица 1
j 1 2 3 4 5 6
cj 112 170 115 50 20 13
aj 28 44 30 16 10 7
Rj=cj /aj 4,0 3,9 3,8 3,1 2,0 1,9
Поскольку решение Хо, обеспечивающее максимум ценностей L(Xo), эквивалентно решению, обеспечивающему максимум удельной эффективности использования общего полезного веса R=L(Xo)/b, то эвристический алгоритм фактически сводится к последовательному отбору предметов в порядке убывания их удельной эффективности (нижняя строка табл. 1). В соответствии с данным правилом получено решение:
X1=(1;0;1;0;0;0), L(X1)=с1+с3=227. (10)
Поскольку для загрузки предмета j=2 оставшегося веса полезной нагрузки (60-28=32 ед.) недостаточно (a2=44 ед.), то подгружается предмет j=3, что и приводит к решению (10), при этом возможна погрешность. Чтобы оценить возможную погрешность сверху, предположим, что существует некий другой вариант загрузки, при котором оставшиеся 32 ед. веса будут использованы с тем же удельным эффектом R2=3,9 ед. Это обеспечит прирост DL=3,9 . 32= 125 ед. и суммарную ценность загрузки Lоц=112+125=237 ед. Тогда оценка сверху (
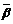 ) возможной относительной погрешности b для варианта x1 будет равна:
) возможной относительной погрешности b для варианта x1 будет равна:
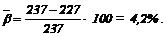
Если полученная оценка для практических целей недопустимо велика, то можно попытаться улучшить решение, выбрав новый (ненулевой) начальный план:
Хнач=(0; 1; 0; 0; 0; 0).
Применяя далее указанный порядок отбора последующих предметов, получим новое решение:
Х2=(0; 1; 0; 1; 0; 0), L(X2)=220.
Поскольку решение Х2 хуже, чем решение Х1, то Х1 полагается оптимальным (подробнее о точности см. в [18, с.150]).
Рассмотренный порядок решения прост и требует минимального объема вычислений, что становится особенно наглядным, если сравнить решение аналогичного примера методом динамического программирования [16, с. 90-93].
Согласно современной теории сложности задача (7)-(9) относится к классу NP-сложных, для которых не существует достаточно эффективных и точных алгоритмов решений, поэтому рассчитывать приходится только на приближенные решения, получаемые с помощью эвристических алгоритмов. Предлагаемый далее алгоритм в основе своей содержит последовательную процедуру отбора предметов по критерию Rj, при этом на каждом шаге процесса множество m ограничений сворачивается к одному, коэффициенты которого (aj) соответствуют дефицитным на данном шаге ресурсам. Достигается это следующим образом.
Каждое ( )из m ограничений- неравенств на t-м шаге процесса умножается на не-
)из m ограничений- неравенств на t-м шаге процесса умножается на не-
кий коэффициент нормировки kit=bt/bit (bt- при-
веденный ресурс). Формально теперь количество ресурса каждого вида стало равно величине, bt (поровну), и, следовательно, наибольший из пронормированных коэффициентов
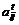 в j-м столбце матрицы êêaij êê, будет соответствовать наиболее быстро убывающему при отборе на погрузку j-го предмета (дефицитному) виду ресурса.
в j-м столбце матрицы êêaij êê, будет соответствовать наиболее быстро убывающему при отборе на погрузку j-го предмета (дефицитному) виду ресурса.
j 1 2 3 4 5 6
t aijt cj 112 170 115 50 20 13 bit+1 kit+1 Lt+1
0 aij 28 44 30 16 10 7 60 1 0
16 20 15 9 8 3 30 2
aij1 28 44 30 16 10 7 16 1
1 32 40 30 18 16 6 10 1,6 170
Rj1 3,5 3,9 3,8 2,8 1,3 1,8 x20=1
aij2 16 10 7 0
2 29 26 9,6 1 220
Rj2 1,7 0,8 0,7 x40=1
При этом расход дефицитного ресурса равен
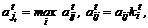 (11)
(11)
где коэффициент норми-
ровки kti=bt/bit (вычисляется на каждом (t-м) шаге процесса); bt- приведенный ресурс, bit-остаток ресурса i-го вида к t-му шагу процесса.
Отбор предмета для погрузки в самолет осуществляется в соответствии с максимумом удельной эффективности Rtj=cj /aj. Далее уточ-няются остатки ресурсов (bt+1), снова задача нормируется, согласно
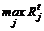 осуществляется отбор очередного предмета и т.д., пока процесс отбора не прекратится вследствие истощения запасов ресурсов. В целом порядок решения обобщенной задачи (7)-(9) можно записать в виде алгоритма:
осуществляется отбор очередного предмета и т.д., пока процесс отбора не прекратится вследствие истощения запасов ресурсов. В целом порядок решения обобщенной задачи (7)-(9) можно записать в виде алгоритма:
1о. Читать êêaij êêmn, (cj)n, êêbi êêm.
2о. t=1.
3о. Нормировать задачу:
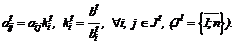 (12)
(12)
4о. Определить Rtj:
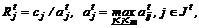 (13)
(13)
5о. Принять 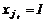 , определив jt из условия:
, определив jt из условия:
 (14)
(14)
6о. Пересчитать: (15)

Jt+1={ jçai j £ b i t+1, j¹ jt ," i}; t=t+1. (16)
7о. Если Jt ¹ Æ, идти к 3о
8о. Писать
 Lmax=L(X0)=Lt. (17)
Lmax=L(X0)=Lt. (17)
9о. Конец.
Работу алгоритма проиллюстрируем на том же числовом примере (табл. 1), добавив к ограничению по весу ограничение по суммарному габариту предметов, заданное неравенством:
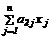 =16x1+20x2+15x3+9x4+6x5+3x6 £ 30,
=16x1+20x2+15x3+9x4+6x5+3x6 £ 30,
где коэффициент a2j – габарит j-го предмета (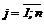 ).
).
Вычислительная схема представлена в виде таблицы 2.
Таблица 2
В верхней части и в рубрике t=0 приведена исходная информация. В правой части записаны текущие значения целевой функции Lt+1, остатков ресурсов bit+1 и нормировочные коэффициенты kit+1. В рубрике t=0 для t+1-го шага имеем k11=1, k21=2. Нормированная согласно (12) матрица коэффициентов aij1 записана в рубрике t=1. Расходы дефицитных ресурсов aj1 в этой матрице выделены жирным шрифтом. Компоненты Rj1 (алг. 4о) записаны в нижней строке (t=1). Согласно 5о получаем x20=1. Остатки ресурсов к t=2-му шагу процесса (6о) записаны в правой части таблицы 2 в рубрике t=1.
Согласно (15) имеем:
b12= b11 - a12 = 60 - 44 = 16,
b22 = b21 - a22 = 30 - 20 = 10.
Из множества номеров переменных
J1={ } (16) убывают те, по которым дальнейшая оптимизация невозможна вследствие малого остатка ресурсов (aij>bit) или потому, что переменная уже получила свое предельное значение (j¹jt). Так, после первого шага имеем J2={4;5;6}. На t=2-м шаге имеем x40=1 (
} (16) убывают те, по которым дальнейшая оптимизация невозможна вследствие малого остатка ресурсов (aij>bit) или потому, что переменная уже получила свое предельное значение (j¹jt). Так, после первого шага имеем J2={4;5;6}. На t=2-м шаге имеем x40=1 (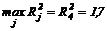 ), и процесс окончен, так как остатка ресурсов недостаточно для дальнейшей оптимизации ни по одной из переменных (J3=Æ,70 ). Полученное решение оптимально:
), и процесс окончен, так как остатка ресурсов недостаточно для дальнейшей оптимизации ни по одной из переменных (J3=Æ,70 ). Полученное решение оптимально:
Хо=(0; 1; 0; 1; 0; 0), L(Xo)=L3=220.
Объем вычислений может быть существенно уменьшен, если на t-м шаге давать единичное приращение не одной переменной, а некоторой их совокупности Gt, соответствующей наибольшим значениям Rjt. Размер этой совокупности может быть определен из условия квантования расхода ресурсов за шаг. Для этого после нормировки задачи следует задать относительную величину a расхода наиболее дефицитного ресурса за один шаг, то есть:
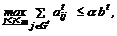 a=0,3-0,6 (18)
a=0,3-0,6 (18)
Это и определит множество Gt. При большой размерности задачи и когда 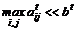 это существенно ускорит процесс решения, без угрозы появления значительной погрешности. Такая угроза возникает лишь при условии, когда остатки ресурсов bit становятся соизмеримы с их удельными расходами aij. Эта ситуация типична для конца процесса оптимизации или при большой начальной дискретности задачи (aij , bi – соизмеримы). Квантование не повлечет за собой существенных изменений алгоритма.
это существенно ускорит процесс решения, без угрозы появления значительной погрешности. Такая угроза возникает лишь при условии, когда остатки ресурсов bit становятся соизмеримы с их удельными расходами aij. Эта ситуация типична для конца процесса оптимизации или при большой начальной дискретности задачи (aij , bi – соизмеримы). Квантование не повлечет за собой существенных изменений алгоритма.
Рассмотренный алгоритм показал хорошую работоспособность. Его возможности могут быть существенно расширены для решения дру-
гих классов задач математического програм-мирования эвристическими методами [18]. Это привлекательно для решения сложных задач на cистемах с элементами искусственного интеллекта.
Список литературы
1. Ловер Ж.-Л. Системы искусственного интеллекта. - М.: Мир,1991.-569 с.
2. Амалия М.,Танака Ю. Архитектура ЭВМ и искусственный интеллект. - М.: Мир,1993.-397 с.
3. Искусственный интеллект. // Под ред. Э.В.Попова. - М.: Радио и связь, 1990.-573 с.
4. Поспелов Д.А. Моделирование рассуждений: опыт и анализ мыслительной деятельности. - М.: Радио и связь, 1989.
5. Поспелов Д.А. и др. Искусственный интеллект. / Справочник в 3-х кн. - М.: Радио и связь. - 1990.
6. Поспелов Г.С. Искусственный интеллект - основа новых информационных технологий. - М.: Наука, 1988.
7. Поспелов Д.А. Ситуационное управление: теория и практика. - М.: Наука, 1986.- 284 с.
8. Поспелов Д.А. Логико-лингвистические модели в системах управления. - М.: Энергоиздат, 1981. - 231 с.
9. Александров Е.А. Основы теории эвристических решений. Подход к изучению естественного и построению искусственного интеллекта. - М.: Сов. радио, 1975.- 254 с.
10. Адамар Ж. Исследование психологии процесса изобретения в области математики. / Пер. с франц. М.А. Шаталовой и О.П. Шаталова. - М.: Сов. радио, 1970. - 151 с.
11. Пойа Д. Математика и правдоподобные рассуждения. - М.: Наука, 1975. 462 с.
12. Колмогоров А.Н. Математика на пороге ВУЗа. Наука сегодня. - М.: Молодая гвардия, 1969.- 224 с.
13. Банди Б. Основы линейного программирования. -М.: Радио и связь, 1989.
14. Юдин Д.Б., Гольштейн Е.Г. Задачи и методы линейного программирования. - М.: Сов. радио, 1964.
15. Методологические основы и математические методы, / Под ред. Дж. Моудера, С. Элмаграби. - М.: Мир, 1981. - Т.1.-712с.
16. Канторович Л.В., Горстко А.Б. Опти-мальные решения в экономике. - М.: Наука, 1972. - 231 с.
17. Волгин Л.Н. Проблема оптимальности в теоретической кибернетике. - М.: Сов. радио, 1968.- 125 с.
18. Берзин Е.А. Оптимальное распределение ресурсов и элементы синтеза систем. - М.: Сов. радио, 1974.- 303 с



 (1)
(1)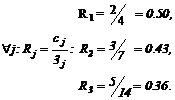 (6)
(6)
