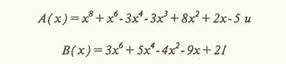Авторитетность издания
Добавить в закладки
Следующий номер на сайте
О некоторых компонентах системы компьютерной алгебры
Аннотация:
Abstract:
| Авторы: Михайлюк М.В. (mix@niisi.ras.ru) - НИИСИ РАН, г. Москва, Москва, Россия, доктор физико-математических наук, Трушина А.А. () - , Петрова И.Н. () - , () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 9499 |
Версия для печати |
Обычной сферой применения высокопроизводительных векторно-коквейерных ЭВМ является решение сложных вычислительных задач, содержащих значительные объемы информации и занимающих большое время счета. Однако в последнее время широкое распространение получают методы решения задач в символьном виде. Это относится в первую очередь к задачам математики, небесной механики, математической физики, физики высоких энергий и т.д., но и в других областях символьные методы приобретают все большее значение. Область исследований, занимающаяся разработкой методов решения задач в символьном виде, обычно называемая компьютерной'алгеброй [2], широка: преобразование и упрощение алгебраических формул, символьное дифференцирование и интегрирование, работа с полиномами, рядами и матрицами с символьными коэффициентами и т.д. В рамках исследований по созданию инструментальных средств и компонент системы компьютерной алгебры, работающей в составе высокопроизводительной вычислительной системы, авторами статьи разработана интегрированная система, включающая меню, редактор, программы синтаксического контроля, преобразования и упрощения формул в соответствии с заданным множеством преобразований, библиотеки функций, осуществляющих арифметические операции над числами произвольной длины. Перед началом работы с системой пользователь имеет возможность выбрать сигнатуру алгебры (множество операций, которые будут встречаться в обрабатываемых алгебраических формулах) и класс носителя (тип чисел, с которыми будут производиться вычисления). В качестве алгебры можно выбрать поле, булеву или любую другую алгебру из систем- ного списка, а в качестве носителя — множество целых, рациональных, действительных или комплексных чисел произвольной длины, причем действительная и мнимая части последних могут быть целыми, рациональными и действительными числами (также произвольной длины). Возможность работы с числами произвольной длины является неотъемлемой частью каждой системы компьютерной алгебры. Известно, что любая ЭВМ работает с целыми числами, величина которых ограничена длиной ячеек памяти. Однако исследования показывают, что при решении реальных задач даже с небольшими величинами исходных данных в результате промежуточных вычислений могут возникать числа, намного превосходящие размеры ячеек ЭВМ. Например, при нахождении последовательности полиномиальных остатков в целых числах для двух полиномов
с помощью модифицированного алгоритма Евклида получается число, занимающее 35 десятичных разрядов. Ясно, что такое число не поместится в обычную ячейку ЭВМ. В результате операции над возросшими числами могут быть выполнены в ЭВМ неверно, что приведет к ошибкам в окончательных результатах, которые довольно трудно обнаружить. Мы моделируем целое число списком, элементы которого являются разрядами представления числа в системе счисления по основанию Ъ = ТЪ где и — разрядность машины. Такие разряды будем называть обобщенными. Старший бит каждого элемента содержит знак числа. Число таких разрядов ограничено лишь памятью ЭВМ (при виртуальной организации - размером внешней памяти) и в этом смысле можно считать, что число имеет имеет неограниченную точность. Рациональное число моделируется парой целых чисел произвольной длины, соответствующих числителю и знаменателю и представляется парой указателей на списки разрядов этих чисел. Действительное число во внутренней структуре хранится в виде длинного целого числа, представляющего мантиссу и порядок числа. Комплексное число имеет структуру дерева, в котором действительная и мнимая части могут быть целыми, рациональными или действительными числами. В любом из этих классов система может выполнять арифметические операции сложения, вычитания, умножения и деления. Все one- рации, производимые над рациональными числами, включают нахождение наибольшего общего делителя числителя и знаменателя я сокращение на него. Тем самым, результирующее рациональное число является уже несократимой дробью. Алгоритмы работы с этими числами описаны в [1, 3]. Все арифметические операции над длинными числами оформлены в виде библиотеки функций, которая может быть подключена к любой прикладной программе. В библиотеку также входят функции перевода во внутреннюю структуру и обратно символьной строки с записанным числом. В случае действительных чисел (или комплексных с действительными коэффициентами) параметром можно задать вид результата, который сформируется в строке либо с фиксированной запятой, либо в экспоненциальной форме, а также указать общее число значащих цифр и цифр после запятой, которые необходимо вывести. При работе с длинными числами и другими элементами системы используется динамическое управление памятью. Интерфейс пользователя с системой осуществляется с помощью подсистемы меню и редактора. Подсистема меню позволяет пользователю в диалоговом режиме без использования языков программирования создать свое дерево меню и обеспечить работу в среде созданного меню. В любом месте дерева меню можно создать новое окно, записать в него имя, характеризующее функцию окна. Этой функции может соответствовать обрабатывающая программа, которую можно подключить к окну, либо целый набор возможностей. В таком случае создается подменю более низкого уровня и подсоединяется к этому окну. Любое окно может быть переименовано или удалено. При этом, если с удаляемым окном связано другое подменю, то соответствующее ему дерево можно либо уничтожить, либо записать в архив. В архиве хранится множество разных подменю, его можно просматривать в динамическом режиме, извлекать нужные части к подсоединять их в места создаваемого меню. Так собираются подменю, созданные различными разработчиками в общее меню системы. По созданному меню системы можно передвигаться и запускать на выполнение подключенные к окнам меню обрабатывающие программы. Очевидно, что подсистема меню является универсальной и может быть использована для создания любых программных продуктов. Б частности, с ее помощью создано меню для компонент системы компьютерной алгебры. Меню системы присутствует на экране дисплея одновременно с окном редактора. Работа системы компьютерной алгебры представляет собой последовательность шагов ввода алгебраической формулы и вывода результата ее преобразования. Редактор обеспечивает все редакторские функции по вводу и корректировке вводимых алгебраических формул. Введенная алгебраическая формула передается обрабатывающей программе, которая_ прежде всего осуществляет ее синтаксический контроль. При наличии синтаксических ошибок управление возвращается редактору с указанием позиции ошибки, отмеченной в редакторе курсором, и ее типа. После исправления ошибки формула опять передается обрабатывающей программе. Обарабатывающая программа в данном случае преобразует и упрощает формулы в соответствии с заложенными в системе и с заданными пользователем изменениями. Результат вместе с управлением вновь передается редактору, который выводит его на экран дли просмотра. Можно также просмотреть весь сеанс работы системы, однако редактор при этом блокирует любые корректировки предыдущих шагов сеанса. Так как в компьютер-нон алгебре широко используются табличные представления данных, то редактор имеет целый ряд специальных средств, позволяющих удобно работать с произвольными таблицами. Как и система меню, редактор является универсальным для обработки иерархической информации и может использоваться в любых других задачах. Подсистема преобразований позволяет пользователю задавать список изменений, которые должны применяться к алгебраическим формулам наряду с обязательными, жестко фиксированными в системе. Примером последних является замена на ноль произведения нуля на любую подформулу или выполнение всех арифметических операций над элементами носителя. В частности, если в формулу в качестве операндов входят только элементы носителя, то система преобразований вычисляет значения формулы, используя базовые программы выполнения арифметических операций с длинными числами заданного носителя. На основе описанных подсистем можно реализовывать различные компоненты системы компьютерной алгебры [4], в частности калькулятор с длинными числами, который вычисляет значение любой формулы из целых, рациональных, действительных и комплексных чисел, арифметических операций и скобок. Реализована также подсистема работы в булевой алгебре, одной из основных задач которой является переход от одного представления булевой функции к другому, например от табличного к представлению в виде формулы или от одного базиса к другому. Немаловажной является также задача минимизации булевой формулы. Разработанная подсистема позволяет задать функцию в виде таблицы истинности, получить по этой таблице символьное представление функции в виде совершенной дизъюнктивной нормальной формы и минимизировать полученную формулу. В соответствии с минимальной формулой можно затем строить управляющие схемы. Система является достаточно универсальной н открытой, что позволяет дополнять и настраивать ее для нужд конкретного пользователя (предполагается ее использование для решения задач математической физики). Программное обеспечиние написано на языке Си. Система может быть использована на ЭВМ типа IBM PC и рабочих станциях, являющихся сателлитами высокопроизводительной векторно-конвейерной ЭВМ. Список литературы 1. Кнут Д. Искусство программирования. М.: Мир, I977.-T.2. 2. Компютерная алгебра. Символьные н алгебраические вычисления / Под ред. Бухбсргсра Б. - М-: Мир, 1986. 3. Михайнюж М.В. Арифметика действительных чисел // Тезисы докладов Всесоки. со вещ. Алгоритмы и програм мы небесной механики. - Л., 1990. 4. Михайлюк М.В., Сотников А.Н., Трушина А.А. On the system of Computer Algebra Operating as a part of Powerful Computer System. // Сб. аннотаций IV Междунар. совещ. по аналитическим вычислениям на ЭВМ в физических ис следованиях. - Дубна, 1990. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1440 |
Версия для печати |
| Статья опубликована в выпуске журнала № 1 за 1992 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Механизм контроля качества программного обеспечения оптико-электронных систем контроля
- Автоматизированная информационная система маркетолога
- Метод интегрированного описания топологических отношений в геоинформационных системах
- К вопросу об информатизации
- Проблемы визуализации и отображения информации
Назад, к списку статей