Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Помехоустойчивые двухэтапные алгоритмы нелинейной фильтрации цифровых изображений
Аннотация:
Abstract:
| Авторы: Самойлин Е.А. (es977@mail.ru) - Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина» (профессор), Воронеж, Россия, доктор технических наук | |
| Ключевые слова: помехоустойчивые алгоритмы, нелинейная фильтрация, цифровые изображения |
|
| Keywords: , , digital images |
|
| Количество просмотров: 11519 |
Версия для печати Выпуск в формате PDF (2.59Мб) |
В последнее время возросло число работ, связанных с развитием теории и программных систем цифровой обработки и преобразования изображений [1–5]. Между тем многие практические условия цифровой регистрации, обработки и хранения изображений становятся причиной появления на растре импульсных помех (ИП), то есть независимых случайных искажений отдельных пикселей. Например, ИП могут возникать при ошибках оцифровки и квантования изображений, сбоях элементов матриц оптико-электронных сенсоров и т.д. [1–3]. Известны и продолжают развиваться достаточно много алгоритмов и методов фильтрации ИП на изображениях, большинство из которых является дальнейшим развитием медианного фильтра, например, адаптация скользящего окна (апертуры) [4] и введение предварительной процедуры оценивания ИП [5]. Последний двухэтапный алгоритм позволяет снизить неизбежные искажения контуров и сигнальных перепадов, так как апертура прикладывается не инвариантно ко всей площади изображения, а исключительно в локальных областях, искаженных ИП. Это позволяет повысить эффективность усредняющей фильтрации, которая традиционно считается неприемлемой для моделей ИП. Между тем алгоритмы [5] показывают хорошие результаты при достаточно низкой интенсивности ИП, когда в апертуре, кроме центрального пикселя, отсутствуют помеховые элементы. В противном случае последние оказывают существенное влияние на результат восстановления (особенно при усреднении), то есть выход фильтра. Цель предлагаемой работы – разработка инвариантных к наличию шумов в апертуре, то есть помехоустойчивых алгоритмов нелинейной фильтрации изображений, искаженных ИП. Рассмотрим модели изображений и ИП, аналогичные описанным в [5]. Используемая модель цифрового (со строками i и столбцами j) изображения
где Значения яркости элементов
где Положив
где
Появления Необходимо синтезировать алгоритм обработки зашумленного изображения
Этап оценивания импульсных помех. Так как амплитуды ИП являются случайными на интервале квантования яркости (5), при оценивании необходимо определить лишь их пространственное положение в пределах матрицы изображения (найти координаты i, j). В работе [5] предложен алгоритм подобного пространственного оценивания ИП, который основан на выделении полезных сигнальных перепадов (за которые принимаются пиксели, содержащие ИП) и последующем отсечении ИП. Работа алгоритма выглядит следующим образом [5]. Шаг 1. Для каждого
где Шаг 2. На основе сумм (6) вычисляется бинарная матрица
Единицы бинарной матрицы Шаг 3. Для отделения элементов ИП от сигнальных перепадов используется свойство связности границ:
где символы Таким образом, результатом первого этапа обработки (6)–(8) будет бинарная матрица оценки помех Этап помехоустойчивого восстановления элементов изображения. Для оптимального в смысле (5) восстановления яркости в координатах помех необходимо центр апертуры прикладывать только к элементам, являющимся в соответствии с (8) ИП (то есть осуществлять пространственно-избирательную фильтрацию [5]), и сигналы восстанавливать по выборке значений апертуры, из которой исключены помехи (8). Указанному требованию удовлетворяют следующие два алгоритма обработки. Алгоритм 1. Усреднение по выборке апертуры из неиспорченных элементов. Шаг 1. Формируется матрица изображения, сбойные в соответствии с (8) элементы которой заменяются на нулевые значения, лежащие вне интервала квантования (для различия с черным цветом):
Шаг 2. На основе усреднения по апертуре (без учета элементов
где В выражении (10), в отличие от известных усредняющих [3] или модифицированного усредняющего [5], усреднению подлежит выборка, из которой полностью исключены элементы помех. Алгоритм (6)–(10), хотя и несколько размывает резкие контуры на изображении, может быть достаточно эффективным при высокой интенсивности ИП (когда в выборке остается 2–5 неиспорченных элементов). Алгоритм 2. Медиана выборки неиспорченных элементов в апертуре. Шаг 1. Аналогично (9) формируется матрица изображения, сбойные в соответствии с (8) элементы которой заменяются на значения, лежащие вне интервала квантования, например, отрицательные:
где Таким образом, полный двухэтапный алгоритм фильтрации – это использование процедуры оценивания ИП (6)–(8) и одного из алгоритмов восстановления сигналов, то есть (9)–(10) либо (11)–(12). Результаты численных исследований. Исследование рассмотренных алгоритмов нелинейной фильтрации проводилось с использованием многочисленных цифровых изображений размером
В качестве критерия оценки качества предлагаемых алгоритмов (ошибки фильтрации) выбрано нормированное евклидово расстояние, вычисляемое для всего диапазона H в соответствии с выражением [6]:
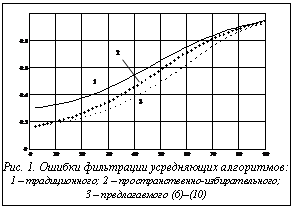
На рисунке 1 приведены результаты расчета критерия (14) в диапазоне интенсивности ИП от 0 до 90 % для трех алгоритмов фильтрации изображений: известного [3] усредняющего, пространственно-избирательного усредняющего, предложенного в [5], и предлагаемого усредняющего алгоритма 1 (6)–(10). Из рисунка 1 следует, что исключение из усреднения элементов, оцениваемых в соответствии с (6)–(8) как помехи, позволяет несколько повысить качество фильтрации (для усредняющих процедур) изображений в диапазоне интенсивности ИП 7–90 %, что объясняется восстановлением испорченных элементов по незашумленной окрестности. Дальнейшее повышение эффективности усредняющих алгоритмов ограничено в силу пространственной инерционности, то есть размазывания контуров на изображениях. На рисунке 2 представлены результаты ана-логичного расчета качества медианных алгоритмов фильтрации: известного инвариантного [1–3], пространственно-избирательного [5] и предлагаемого (11)–(12). Из рисунка 2 следует, что предлагаемый алгоритм является более эффективным, чем срав- ниваемые в диапазоне интенсивности ИП 10–65 %. Причем основное повышение качества фильтрации достигается при H=10–30 %.
Предложенные двухэтапные алгоритмы нелинейной фильтрации импульсных помех на цифровых изображениях являются более эффективными, чем аналогичные известные, так как восстановление сигналов происходит по выборке окрестности, из которой исключены элементы, оцениваемые как помехи на предварительном этапе обработки. Алгоритмы достаточно легко реализуются программно и могут использоваться во многих информационных системах с цифровой обработкой изображений. Список литературы 1. Гонсалес Р., Вудс Р. Цифровая обработка изображений. – М.: Техносфера, 2005. – 1072 с. 2. Сойфер В.А., Гашников М.В., Глумов Н.И. и др. Методы компьютерной обработки изображений. – М.: Физматлит, 2001. – 784 с. 3. Дьяконов В.П., Абраменкова И.В. MATLAB. Обработка сигналов и изображений. Специальный справочник. – СПб: Питер, 2002. – 608 с. 4. Воскобойников Ю.Е., Кузнецов А.М. Новый алгоритм адаптации размера апертуры локальных векторных фильтров. // Автометрия, 2005. – Т. 41. – № 5. – С. 3. 5. Самойлин Е.А. Программно-реализуемые алгоритмы нелинейной фильтрации цифровых изображений. // Программные продукты и системы. – 2006. – № 4. – С. 7–9. 6. Самойлин Е.А. Оценка эффективности программных методов обработки изображений. // Программные продукты и системы. – 2003. – № 4. – С. 34–37. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1593 |
Версия для печати Выпуск в формате PDF (2.59Мб) |
| Статья опубликована в выпуске журнала № 3 за 2008 год. | |
| Статья находится в категориях: Обработка данных, Программно-аппаратные средства | |
| Статья относится к отраслям: Вычисления | |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



 имеет вид:
имеет вид: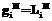 , (1)
, (1) – непрерывное изображение, соответствующее
– непрерывное изображение, соответствующее  – интервалы дискретизации для i, j соответственно;
– интервалы дискретизации для i, j соответственно; 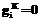 ,
, 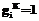 ,
, 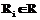 – количество i и j.
– количество i и j.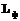 ,
, 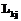 и т.д., (2)
и т.д., (2)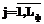 – количество уровней квантования яркости сигналов
– количество уровней квантования яркости сигналов 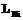 ,
,  , запишем выражение для ИП:
, запишем выражение для ИП: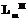 (3)
(3) – вероятность появления полезного сигнала
– вероятность появления полезного сигнала  в ячейке с координатой
в ячейке с координатой 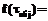 ;
; 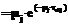 – значения искаженных элементов изображения, которые являются независимыми случайными величинами с равномерным распределением (
– значения искаженных элементов изображения, которые являются независимыми случайными величинами с равномерным распределением (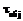 ), соответствующими интервалу квантования (2):
), соответствующими интервалу квантования (2): ,
, 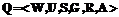 – вероятность появления помехи
– вероятность появления помехи 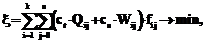
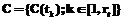 .
.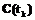 , описываемого выражением (3), позволяющий сформировать такую оценку
, описываемого выражением (3), позволяющий сформировать такую оценку 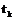 изображения, которая была бы наиболее близка к ее истинным значениям:
изображения, которая была бы наиболее близка к ее истинным значениям: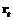 . (5)
. (5)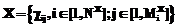 , (6)
, (6)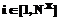 – параметры апертуры, определяющие ее размер по i и j соответственно (3´3 элемента).
– параметры апертуры, определяющие ее размер по i и j соответственно (3´3 элемента).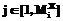 сигнальных и помеховых перепадов:
сигнальных и помеховых перепадов: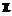 (7)
(7)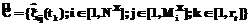 (8)
(8)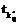 и
и  означают процедуры «Логическое И» и «Логическое ИЛИ» соответственно.
означают процедуры «Логическое И» и «Логическое ИЛИ» соответственно.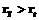 , единицы которой соответствуют координатам ИП
, единицы которой соответствуют координатам ИП  (9)
(9) (10)
(10) – количество сбойных элементов (
– количество сбойных элементов (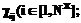 ) в апертуре, не считая центрального, который, по условию в первой строке (10), равен 1,
) в апертуре, не считая центрального, который, по условию в первой строке (10), равен 1, 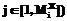 .
.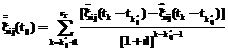 (11)
(11) Шаг 2. Сбойные элементы восстанавливаются по медиане выборки, из которой исключены значения помех, определяемые по
Шаг 2. Сбойные элементы восстанавливаются по медиане выборки, из которой исключены значения помех, определяемые по 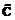 (12)
(12)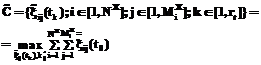 – левое срединное (то есть ближайшее слева к середине) значение ряда в случае четного числа элементов выборки;
– левое срединное (то есть ближайшее слева к середине) значение ряда в случае четного числа элементов выборки;  – правое срединное значение. Таким образом, при четном числе положительной после (11) выборки ее медиана представляет собой среднее арифметическое двух центральных значений элементов при упорядочении по возрастанию.
– правое срединное значение. Таким образом, при четном числе положительной после (11) выборки ее медиана представляет собой среднее арифметическое двух центральных значений элементов при упорядочении по возрастанию. и N=8. Перед фильтрацией изображения подвергались целенаправленному зашумлению ИП в соответствии с выражением (3). Исследование проводилось в диапазоне интенсивности ИП от 0 до 100 %, которая определялась из выражения:
и N=8. Перед фильтрацией изображения подвергались целенаправленному зашумлению ИП в соответствии с выражением (3). Исследование проводилось в диапазоне интенсивности ИП от 0 до 100 %, которая определялась из выражения: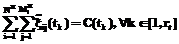 . (13)
. (13)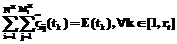 . (14)
. (14)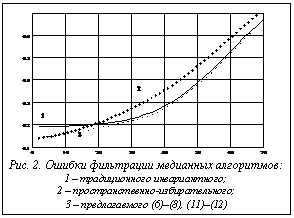 Приведенные на рисунках численные результаты являются усредненными по выборке из более чем 100 цифровых изображений с различными пространственными частотами. Вычислительные эксперименты и программная реализация алгоритмов проведены в среде MathCAD 11.
Приведенные на рисунках численные результаты являются усредненными по выборке из более чем 100 цифровых изображений с различными пространственными частотами. Вычислительные эксперименты и программная реализация алгоритмов проведены в среде MathCAD 11.