Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование температурных полей в многослойных структурах
Аннотация:
Abstract:
| Авторы: Мадера А.Г. (alexmadera@mail.ru) - НИИСИ РАН (профессор, зав. отделом), г. Москва, Россия, доктор технических наук, Кандалов П.И. (petrki87@gmail.com) - НИИСИ РАН (зам. зав. отделом), Москва, Россия | |
| Ключевые слова: моделирование, температурное поле, микросхемы |
|
| Keywords: modeling, a tempering, microchips |
|
| Количество просмотров: 17994 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
Важнейшие характеристики электронных изделий (ЭИ) и их элементов (микросхем, электронных модулей (ЭМ), вычислительных комплексов и систем и др.), такие как статические и динамические электрические параметры, надежность, быстродействие, помехоустойчивость и прочее, в значительной степени зависят от температуры. Причем ограничения по уровню рабочей температуры ЭИ являются существенными и зачастую решающими на пути создания ЭИ с требуемыми значениями эксплуатационных характеристик и параметров. Перегревы могут приводить к выходу микросхем из строя, их неправильному срабатыванию, низкой надежности и т.д. Поэтому наряду с проектированием ЭИ (кристаллов микросхем, корпусов микросхем, многослойных печатных плат с установленными на них микросхемами, электронных модулей и др.) необходимо проводить также и тепловое проектирование ЭИ, которое охватывает все проблемы, связанные как с моделированием значений температуры в различных точках ЭИ (температурных полей) при различных условиях эксплуатации и испытаний проектируемых ЭИ, так и с конструированием и проектированием эффективных систем теплоотвода и охлаждения ЭИ. Моделирование температурных полей элементов ЭИ и всех ЭИ в целом позволяет выявлять наиболее критические и перегревающиеся элементы еще на этапе проектирования ЭИ и выдавать научно обоснованные рекомендации по выбору параметров микросхем, конструкции корпусов, по расположению микросхем на печатной плате, конструкции печатных плат и электронных модулей, стоек ЭИ и др. Отметим также, что тепловое проектирование является обязательным этапом при проектировании ЭИ в ведущих мировых компаниях, занятых разработкой и производством ЭИ. Моделирование тепловых процессов в ЭИ –достаточно сложная проблема. Это проявляется уже в том, что на сегодняшний день отсутствуют надежные, адекватные и универсальные программные средства компьютерного моделирования тепловых процессов сложных ЭИ. Так, известный программный комплекс Beta-Soft, предназначенный для моделирования температурных полей в ЭИ, может рассчитывать многослойные печатные платы только с тремя слоями. Между тем, современные печатные платы насчитывают десятки слоев, каждый из которых имеет различные теплофизические характеристики. Сложность проблемы математического и компьютерного моделирования тепловых процессов обусловливается тем, что конструкции ЭИ – сложные системы, состоящие из большого числа элементов, многие из которых сами являются подсистемами. Так, каждая микросхема, входящая в состав ЭМ и расположенная на печатной плате, представляет собой сложную систему, состоящую из кристалла с созданной на его поверхности системой p-n-переходов металлизированной разводкой, из корпуса микросхемы, выводов кристалла и корпуса, элементов теплоотвода и системы охлаждения. Элементы ЭИ характеризуются различными значениями потребляемых мощностей, размерами и пространственными конфигурациями, всевозможными теплофизическими характеристиками материалов, неоднородными включениями и полостями, динамикой распределения потребляемых элементами мощностей как во времени, так и в пространстве, и т.д. Таким образом, температурные поля, возникающие в ЭИ, являются неоднородными, трехмерными и нестационарными. Кроме того, важнейшие элементы ЭИ, определяющие работоспособность и эксплуатационные характеристики всей ЭИ в целом (печатные платы и микросхемы), представляют собой многослойные структуры, состоящие из большого числа слоев, имеющих различную толщину и выполненных из разнородных материалов. Температурные поля многослойных структур являются трехмерными и неоднородными, что обусловливается, во-первых, неравномерным расположением микросхем на плате, во-вторых, разным конструктивным исполнением микросхем и различными значениями потребляемых микросхемами мощностей и, в-третьих, многослойной структурой печатной платы и микросхем. Поэтому моделирование температурных полей многослойных структур ЭИ – чрезвычайно важная и актуальная проблема. В настоящей работе описаны методы математического и компьютерного моделирования трехмерных температурных полей в многослойных структурах ЭИ (многослойных печатных плат (МПП), микросхем, теплоотводов и др.). С помощью разработанных методов проведено моделирование стационарных температурных полей в МПП с установленными на ее верхней и нижней поверхностях микросхемами и электрорадиоэлементами (ЭРЭ). Кроме того, исследовано влияние тонких теплопроводящих слоев в МПП (выполненных из меди) на температурное поле печатной платы и микросхем.
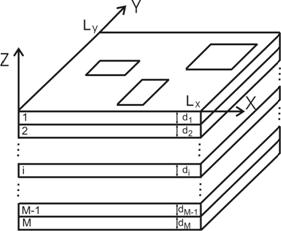
Рис. 1. Тепловая модель МПП для расчета стационарного температурного поля Математическая и тепловая модели многослойной структуры ЭИ Тепловая модель многослойной структуры (рис. 1) представляет собой прямоугольный многослойный параллелепипед, моделирующий МПП, с размерами Lx и Ly по осям X и Y и слоями i=1,2,…,M толщиной di и коэффициентом теплопроводности li. На верхней и нижней поверхностях многослойного параллелепипеда расположены прямоугольные источники теплоты, моделирующие микросхемы и ЭРЭ, каждый из которых определяется своей величиной потребляемой мощности, геометрическими размерами и расположением центра источника на плате. Так как теплоотдача с горизонтальных поверхностей МПП значительно превышает теплоотдачу с торцов, в математической модели принято, что боковые торцы МПП теплоизолированные. Математическая модель, описывающая стационарное температурное поле в тепловой модели, содержит: · систему из М уравнений теплопроводности для каждого i-го слоя:
· граничные условия: - на верхней поверхности параллелепипеда (i=1):
- на нижней поверхности параллелепипеда (i=M):
- на границе i-го и i+1-го слоев:
- на боковых торцах параллелепипеда:
где Математическое и компьютерное моделирование Уравнения математической модели (1)–(6) удается решить в аналитическом виде и получить аналитические выражения для температурного поля в любой точке слоев в многослойной тепловой модели. Аналитическое решение математической модели получено методом конечных интегральных преобразований, а именно, методом двойного косинус-преобразования Фурье, и имеет вид:
где
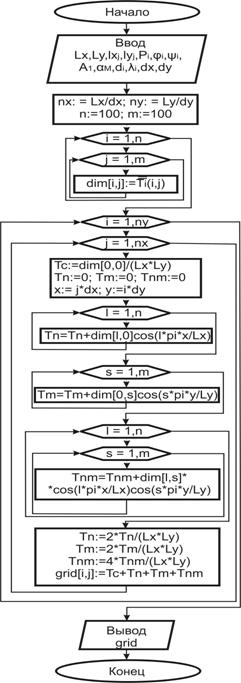
Компьютерное моделирование полученного аналитического решения математической модели (1)–(6) реализовано на языке высокого уровня Delphi с применением объектно-ориентированного программирования (ООП). Это позволяет разрабатывать системы для многократного использования, разложить программу на отдельные блоки и сделать ее более понятной. Алгоритм компьютерного моделирования представлен на рисунке 2.
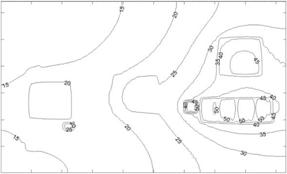
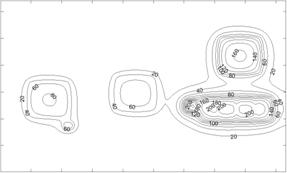
Рис. 2. Алгоритм компьютерного моделирования трехмерных температурных полей многослойных структур: dim – массив значений образа температуры для различных m и n; grid – массив температур (температурная сетка); nx, ny – количество узлов в сетке по координатам X и Y соответственно. Влияние высокотеплопроводных слоев на температурное поле многослойной структуры ЭМ С помощью разработанных методов математического и компьютерного моделирования были проведены исследования реальной конструкции ЭМ, состоящей из МПП с 23 слоями и 15 микросхемами с различными размерами корпусов и потребляемой мощностью. МПП представляет собой много- слойную структуру, состоящую из 6 медных слоев толщиной 0,017 мм, 11 слоев, выполненных из полиимида толщиной 0,2 мм, и 6 слоев металлизированной разводки толщиной 0,017 мм. Слои с металлизированной разводкой являются композитными неоднородными структурами, состоящими из полиимида и медных проводников. Рассчитанное температурное поле многослойной структуры ЭМ представлено на рисунке 3 в виде линий уровня температуры (изотерм). Максимальная температура, равная 50°, имеет место на микросхеме, расположенной в окружении четырех аналогичных микросхем рядом с микросхемой наибольшей мощности потребления (10 Вт). Для исследования влияния теплопроводящих слоев на температурное поле ЭМ было проведено также моделирование ЭМ, когда высокотеплопроводные (медные) слои в многослойной структуре печатной платы отсутствуют. Изотермы для рассматриваемого случая приведены на рисунке 4. Из анализа полученных данных следует, что максимальная температура соответствует той же микросхеме, что и в первом случае, однако ее уровень в несколько раз выше и составляет 220°.
Рис. 3. Изотермы температурного поля при наличии 6 медных слоев в печатной плате
Рис. 4. Изотермы температурного поля при отсутствии медных слоев в печатной плате Результаты моделирования показывают, что наличие в МПП тонких высокотеплопроводных слоев (0,017 мм) значительно уменьшает уровень максимальных температур как на печатной плате, так и на поверхности микросхем. Это обусловливается тем, что введение в структуру МПП слоев из высокотеплопроводных материалов (в рассматриваемом случае – из меди) даже малой толщины (0,017 мм) значительно расширяет площадь растекания теплоты, тем самым увеличивая рассеяние теплоты в окружающую среду. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1611 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
| Статья опубликована в выпуске журнала № 4 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программа идентификации условий теплообмена для изделий плоской формы
- Программы моделирования и идентификации температурных полей в сортовых стеклоизделиях
- Программы моделирования температурных полей в изделиях цилиндрической формы
- Программы моделирования температурных полей в изделиях плоской формы
- Модель радиационных эффектов воздействия тяжелых заряженных частиц в КМОП-элементах микросхем
Назад, к списку статей



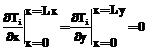 , (6)
, (6)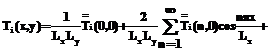
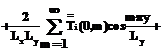 (7)
(7)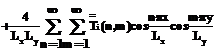 ,
,