Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм прогнозирования ресурса электроконтактного соединения
Аннотация:
Abstract:
| Авторы: Измайлов В.В. () - , Наумов А.Е. () - , Новоселова М.В. () - | |
| Ключевые слова: электроконтактное соединение, оборудование, алгоритм |
|
| Keywords: , , algorithm |
|
| Количество просмотров: 11876 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
Своевременное предсказание аварийного состояния электротехнического оборудования позволяет принимать предупреждающие меры. Необходимым элементом электрических сетей являются неподвижные разъемные и неразъемные контакты. Статистика показывает, что отказ электроконтактных соединений часто является причиной серьезных аварий на электрических сетях. Одним из путей решения задачи раннего выявления деградационного отказа электроконтактного соединения является прогнозирование его технического состояния по результатам наблюдения в процессе эксплуатации. Задача прогнозирования опирается на сложные математические или эмпирические методы поиска закономерностей в рассматриваемом временном процессе. В матема- тической статистике имеются развитые методы анализа и прогнозирования временных рядов, например, модель Бокса–Дженкинса (ARIMA). Недостатком этой и других подобных моделей являются требования, которые они предъявляют к анализируемому процессу, например, требование стационарности процесса, что на практике, как правило, не выполняется. Следует отметить общий недостаток чисто статистических методов – они не учитывают физической природы анализируемого процесса.
Рис. 1 На основании математической модели старения электроконтактного соединения (см.: Braunovic M., Izmailov V.V., Novoselova M.V. A Model for Life Time Evaluation of Closed Electrical Contacts. // Proceedings of the 51 IEEE Holm Conference on Electrical Contacts. Chicago, 2005, pp. 217–223), базирующейся на предположении о диффузионном механизме окисления контакта и последующем росте контактного сопротивления, получена зависимость сопротивления контакта от времени:
где tm – предельная величина времени жизни контакта (ресурс контактного соединения); k=R(t)/R0 – параметр, характеризующий относительное увеличение сопротивления; R(t) – текущее значение сопротивления; R0 – начальное значение сопротивления; a и b – параметры, характеризующие геометрию и состояние контактирующих поверхностей. Формула (1) послужила основой для предлагаемого метода прогнозирования ресурса электроконтактного соединения. Исходными параметрами в данной методике прогнозирования являются два значения параметра k: значение kl задает предельно допустимый рост контактного сопротивления, при котором наступает параметрический отказ; значение kс играет роль текущего контрольного сигнала для самокорректировки модели. Момент времени tс, когда ожидается рост сопротивления контакта в kс раз, рассчитывается по формуле, вытекающей из уравнения (1):
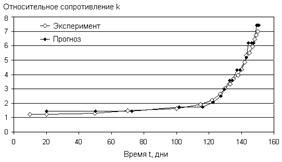
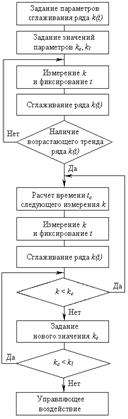
Укрупненная структурная схема предлагаемой методики прогнозирования ресурса электроконтактного соединения приведена на рисунке 1. Для построения прогноза различные члены временного ряда R(t) или k(t) имеют разную информационную ценность: свежие наблюдения более важны, чем старые. Для придания различного веса экспериментальным данным, а также для исключения незначительных случайных флуктуаций сопротивления необходимо производить сглаживание (экспоненциальное или скользящее среднее) исходного ряда R(t). Возможности предлагаемой методики иллюстрируются на при мере реального соединения питающего ка- беля с клеммой электрического аппарата (рис. 2). Задаем контрольный уровень kс=1,2 (то есть увеличение сопротивления на 20 %). Периодически измеряем сопротивление R в фиксированные моменты времени t и проверяем полученный ряд k(t) на наличие возрастающего тренда. При отсутствии возрастающего тренда прогноз не производится, а идет накопление экспериментальных данных. Через 7 дней наблюдений зафиксирован рост сопротивления на 20 %, то есть k(7)=1,2 (рис. 2). Задаем новый контрольный уровень kс=1,4 (то есть увеличение сопротивления еще на 20 %). Рассчитываем по формуле (2) время следующего измерения сопротивления tс, через которое прогнозируется относительный рост сопротивления до величины контрольного уровня kс=1,4. Это время составляет 20 дней от начала наблюдений. Измеряем сопротивление в 20-й день от начала наблюдения. Значение относительного сопротивления k(20) меньше контрольного уровня kс=1,4. Проводим уточнение прогноза момента tс с учетом текущего экспериментального значения k(20). Согласно (2) это время теперь составляет 50 дней. Измеряем сопротивление в 50-й день от начала наблюдения. Величина k(50) также меньше контрольного уровня kс=1,4. По текущему значению k(50) рассчитываем следующий контрольный момент tс=70 дней. Измеряем сопротивление в 70-й день от начала наблюдений. Измеренный рост сопротивления k(70) достиг контрольного уровня kс=1,4. Задаем следующий контрольный уровень, например kс=1,7 (то есть увеличение сопротивления еще примерно на 20 %).
Рис. 2 Описанная выше процедура повторяется, пока очередное значение контрольного уровня kс не достигнет предельно допустимого kl, что послужит сигналом о приближении отказа контактного соединения и о необходимости управляющего воздействия для его предотвращения. Данная задача может решаться в автоматическом режиме с применением современных программных средств и способов визуализации данных, в том числе с помощью разработанной авторами компьютерной программы «Система обработки и анализа данных тепловизионного контроля электроконтактных соединений» (свидетельство об официальной регистрации программы ЭВМ № 2008610197). Область применения описанного алгоритма не ограничивается электроконтактными соединениями. Методика применима к любым объектам и изделиям, подверженным постепенным (деградационным) отказам. Для прогнозирования ресурса необходимо на основании исследования физических процессов, приводящих к деградационному отказу объекта, выбрать ресурсный параметр Y(t) (в описанной методике – контактное электросопротивление) и установить закономерность его изменения во времени. Учитывая, что практически всегда значения ресурсного параметра будут подвержены случайным флуктуациям, модель прогнозирования должна сочетать физические и статистические подходы, в частности, сглаживание временного ряда Y(t). Описанный алгоритм позволяет прогнозировать ресурс данного объекта на основании мониторинга его технического состояния в процессе эксплуатации. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1638 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
| Статья опубликована в выпуске журнала № 4 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Способы реализации алгоритмов интегральных преобразований изображений по линиям
- Комплекс программ идентификации точечных дефектов листового стекла
- Рекурсивный алгоритм точного расчета ранговых критериев проверки статистических гипотез
- Эффективная программная реализация вейвлет-преобразования
- Метод повышения адекватности модели общекорабельных систем для тренажеров
Назад, к списку статей



 . (2)
. (2)