Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Об одном подходе к управлению многопродуктовыми запасами
Аннотация:
Abstract:
| Авторы: Хоботов Е.Н. (e_khobotov@mail.ru) - Московский государственный технический университет им. Н.Э. Баумана, Москва, Россия, доктор технических наук, Калинин Н.М. () - | |
| Ключевые слова: модель, учет товаров, управление запасами |
|
| Keywords: mathematical model, , inventory management |
|
| Количество просмотров: 10521 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
Проблемам управления запасами уделяется повышенное внимание, вызванное расширением торговли и, соответственно, ростом объема товарооборота в различных отраслях и регионах. Вместе с этим растут и объемы средств, вложенных в создание запасов, а также затраты на их поддержание и обслуживание. Однако во многих случаях можно сократить затраты, связанные с организацией и хранением запасов, за счет правильного выбора объема и времени его пополнения [1–3].
В настоящее время на российском рынке достаточно много программных продуктов, способствующих повышению качества и эффективности процессов обеспечения потребителей различной продукцией. В них хорошо представлены функции учета и движения товаров, однако функции по определению объемов и времени пополнения запасов, которые позволили бы сократить затраты на хранение и организацию поставок, представлены слабо либо вовсе отсутствуют. Основная причина – недостаточная разработка моделей и методов управления многопродуктовыми запасами. В данной разработке для управления многопродуктовыми запасами предлагается принцип построения математических моделей, позволяющих определять объемы пополнения запасов и время между смежными пополнениями запасов в условиях постоянного и случайного спроса. В случае постоянного спроса на продукцию с использованием разработанных моделей удается получать оптимальные решения, а в условиях случайного спроса такие модели демонстрируют высокую эффективность. Модели управления запасами при постоянном спросе Одной из самых известных и распространенных моделей для определения объема пополнения запасов, когда на складе хранится продукция одного типа, является модель Уилсона–Харриса (см., например, [1–3]). Выражение для величины оптимального пополнения запасов q* в этой модели имеет вид:
Рис. 1. График изменения величины запасов при использовании формулы Уилсона–Харриса для продукции одного типа
Рис. 2. График изменения величины запасов при использовании формулы Уилсона–Харриса для разной продукции
Рис. 3. График изменения величины запасов при одновременной поставке разной продукции Здесь Cs – затраты, связанные с доставкой, оформлением и размещением продукции и не зависящие от объема пополнения запасов q*; R – количество продукции, которое реализуется потребителям в течение периода планирования T; c1 – стоимость хранения единицы продукции в единицу времени. Процесс изменения величины запасов в этом случае можно представить графически (рис. 1). При наличии разнообразной продукции использование данной формулы затруднительно, поскольку для каждого вида будут определены своя оптимальная величина закупаемого пополнения запаса и свое время возобновления поставки. Графически изменение величины запасов при таких условиях можно представить в виде, показанном на рисунке 2. Для преодоления таких затруднений возникает идея производить закупку и доставку на склад продукции нескольких типов одновременно, чтобы к началу следующей поставки запасы этой группы продуктов стали равными нулю. Графически процесс изменения величины запасов при таком предположении представлен на рисунке 3. Затраты на хранение продукции между пополнениями запасов ts составят: Поскольку спрос Предположим также, что в течение интервала планирования T производится целое количество пополнений запасов n. Исходя из сделанных предположений, суммарные затраты на хранение и организацию поставки для группы продуктов принимают вид:
где Подставив выражения для n и
Функция Из этих условий и определяется оптимальное время между смежными пополнениями склада
Тогда в соответствии с выражениями, определяющими величины qi, получим:
Здесь, однако, возникают проблемы, связанные с тем, что при увеличении количества продукции, хранящейся на складе, увеличивается знаменатель в соотношениях (3) и (4). Если остальные параметры задачи не меняются, это приводит к сокращению времени между закупками и величины закупок и к увеличению количества закупок. Во многих случаях не все параметры в задачах управления запасами задаются явно. Например, очень часто задается годовая стоимость аренды склада и оцениваются эксплуатационные расходы на содержание склада и хранение продукции в течение определенных интервалов времени. Стоимость же хранения единицы продукции в единицу времени, которая используется в соотношениях (3) и (4), часто не задается явно, поскольку, как уже отмечалось выше, задается общая стоимость аренды всего или части склада на определенный, обычно продолжительный, срок. Поэтому величина стоимости хранения продукции различных типов в единицу времени в таких случаях оказывается внутренним параметром, который владельцы или арендаторы склада могут выбирать с учетом каких-либо своих целей или потребностей. С другой стороны, стоимость хранения продукции, как видно из соотношений (3) и (4), является весьма важным параметром для управления запасами. Кроме того, в подобных задачах часто бывают уже известными и объемы арендованных складов. В связи с этим возникает дополнительная задача, связанная с определением уровня заполнения склада продукцией. Стоимость хранения продукции в подобных случаях оказывается важным параметром, который будет определять время между смежными пополнениями запасов и уровень заполнения склада продукцией. Величину стоимости хранения продукции целесообразно определять еще и с учетом стоимости аренды, эксплуатационных расходов и минимизации затрат на хранение и пополнение запасов. Необходимо также учитывать величину доступных оборотных средств, которые выделяются на разовую покупку продукции для пополнения запасов. Величина пополнения склада не должна превышать объема склада Q и затрат на разовое пополнение склада P, что приводит к ограничениям следующего вида:
Затраты на хранение продукции в течение планового интервала T должны быть достаточными для оплаты аренды склада
Из соотношений видно, что выбирать можно не величины Принципы построения моделей управления запасами при случайном спросе При построении подобных моделей будем считать, что время поставки заказа является детерминированной, а не случайной величиной. Рассмотрим случай, когда дефицит продукции на складе нежелателен. При постоянном спросе в аналогах подобных моделей для одного продукта дефицит на складе не допускается [1,3]. В условиях случайного спроса гарантировать отсутствие дефицита продукции на складе невозможно, но подобные модели могут быть модифицированы и для этих вариантов. Для случая постоянного спроса уже были выведены соотношения, позволяющие определять оптимальное время между смежными закупками продукции (соотношение (3)) и величину оптимальных закупок При наличии случайного спроса использование этой формулы затруднительно, поскольку спрос Приведенные выше соотношения с некоторыми изменениями могут быть использованы и в условиях случайного спроса. Пусть спрос на продукцию в течение некоторого интервала T является стационарным и среднее значение спроса для i-го продукта в течение этого времени равно Для сокращения затрат на содержание запасов в процесс управления, как уже отмечалось, целесообразно ввести обратную связь, которая может сократить остатки продукции или их нехватку на складе к моменту следующего пополнения запасов. Для этого величину закупок В задачах со случайным спросом величины Однако в задачах со случайным спросом необходимо еще проверять величину каждого пополнения запасов на выполнение ограничений по объему склада Q и по затратам на разовое пополнение склада P при конкретных величинах закупок qki. С разработанными моделями были проведены вычислительные эксперименты как на тестовых исходных данных, так и на данных, любезно предоставленных одной из фирм, связанных с созданием и хранением запасов. Проведенные вычислительные эксперименты показали достаточно высокую эффективность разработанных моделей в условиях постоянного и случайного спроса. Список литературы 1. Хедли Д., Уайтин Т. Анализ систем управления запасами. – М.: Наука, 1969. – 511 с. 2. Рыжиков Ю.И. Теория очередей и управление запасами. – СПб: Питер, 2001. – 384 с. 3. Хоботов Е.Н. Управление в технических системах. Ч. I. Управление запасами.: Учеб. пособ. – М.: МГТУ им. Н.Э. Баумана, 2001. – 96 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=1639 |
Версия для печати Выпуск в формате PDF (8.40Мб) |
| Статья опубликована в выпуске журнала № 4 за 2008 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Информационное обеспечение процессов развития больших систем административно-организационного управления
- Прогнозирование временного ряда инфекционной заболеваемости
- Моделирование информационных ресурсов при процессной организации системы управления предприятием
- Факторный анализ в задачах моделирования многомерных систем
- Модель формирования адаптивной среды обучения и оценка ее эффективности
Назад, к списку статей






 . (3)
. (3)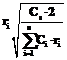 . (4)
. (4)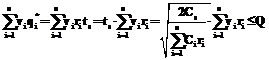 ,
,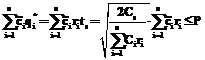 .
.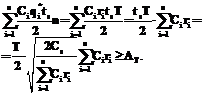 .
.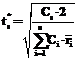 .
. , где
, где 