Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Модель высвобождения активных веществ из нанопористых тел
Аннотация:
Abstract:
| Авторы: Меньшутина Н.В. (chemcom@muctr.ru) - Российский химико-технологический университет им. Д.И. Менделеева (профессор), г. Москва, Россия, доктор технических наук, Гуриков П.А. (chemcom@muctr.ru) - Российский химико-технологический университет им. Д.И. Менделеева, Москва, Россия, кандидат технических наук, Колнооченко А.В. () - | |
| Ключевые слова: программа параллельных вычислений, высокопористые тела, процессы адсорбции–десорбции, методы описания динамических систем |
|
| Keywords: , , , |
|
| Количество просмотров: 8697 |
Версия для печати Выпуск в формате PDF (3.60Мб) |
Многие процессы при физическом моделировании описываются дифференциальными уравнениями в частных производных. Методы численного решения таких уравнений давно разработаны, и для них существуют эффективные алгоритмы. Однако зачастую простые уравнения имеют сложные граничные условия, что вызывает серьезные трудности при их решении. Такие условия часто встречаются при описании массо- и теплопереноса, динамики биологических популяций, движений толпы в чрезвычайных ситуациях и ряде других задач.
Рис. 1. Добавление новой сферы. Расстояние между сферами уменьшается до В последние годы активно разрабатываются новые методы для описания динамических систем различной природы, которые не основаны на решении дифференциальных уравнений. Такими инструментами являются клеточные автоматы, метод Монте-Карло, теория перколяции и другие. В настоящей работе клеточными автоматами описывается динамика высвобождения молекул лекарственного (активного) вещества из пористой матрицы в раствор. Это позволяет прогнозировать концентрацию активных веществ в организме и добиваться наиболее значительного терапевтического эффекта. Задачи, аналогичные рассмотренным, возникают при моделировании сушки пористых тел (древесина, керамика), набухания капиллярных тел, процессов адсорбции–десорбции в химической технологии. В работе [1] в качестве пористой матрицы-носителя изучаются аэрогели – высокопористые тела на основе диоксида кремния с чрезвычайно низкой плотностью (до 0,001 г/см3). Аэрогели нетоксичны, процесс их получения сравнительно дешев. Однако связь между кинетическими характеристиками высвобождения, структурой аэрогеля и химическим строением активного вещества до сих пор не установлена и носит в лучшем случае эмпирический характер.
Рис. 2. Перенесение шара на кубическую сетку (сечение) В настоящей работе предлагается модель структуры с заданной степенью пористости, имитирующей структуру реального аэрогеля. Для моделирования высвобождения (десорбции) активного вещества в жидкую среду используется метод клеточных автоматов с окрестностью Марголуса. Для обеих моделей разработаны алгоритмы и их программная реализация. Модель слабо перекрывающихся сфер Многочисленными экспериментами установлено, что структура аэрогеля представляет собой систему твердых глобул (шаров) диоксида кремния диаметром 2–10 нм. Пространство между ними образует систему пор. Доля свободного пространства, приходящегося на поры, в зависимости от способа получения аэрогеля составляет от 50 до 95 %. В предложенной модели глобулы диоксида кремния моделируются жесткими шарами постоянного радиуса. Алгоритм построения структуры состоит из следующих шагов. 1. Создание набора шаров N одинакового диаметра d=2r, перекрывающихся между собой не более чем на определенную величину ψ. Первый и последующие шары задаются тройкой случайных координат их центра. Если вновь созданный шар перекрывается с соседним более чем на ψd, то он перемещается вдоль линии, соединяющей центры атомов, до тех пор, пока перекрывание не уменьшится до величины ψ (рис. 1). Всякий раз после добавления нового шара вычисляются объем, занимаемый шарами, и пористость – как доля свободного объема. Критерием перехода к шагу 2 является достижение заданной пористости. Если число попыток добавить новый шар превышает наперед заданное критическое значение Kmax, считается, что достигнута плотнейшая упаковка, и программа переходит к шагу 2. 2. Из сгенерированного набора шаров удаляются произвольно выбранные сферы. Так как структура реального аэрогеля представляет собой систему связных шаров, критерием возможности удаления частицы является сохранение перколяционного кластера в рассматриваемом объеме. Условие связности проверяется с помощью модифицированного алгоритма маркировки кластеров Хошена–Копельмана. Процесс завершается при достижении заданного значения пористости. Если ни один шар нельзя удалить без разрушения перколяционного кластера, а заданная пористость еще не достигнута, пользователю предлагается повторить шаг 2. Поскольку полученная на шаге 2 структура далее будет использована в методе клеточного автомата, ее необходимо перенести на кубическую сетку. Ячейка, в которой находится центр шара, и все ее соседи, стоящие не более чем на r, помечаются как занятые диоксидом кремния (рис. 2). В экспериментальных исследованиях высвобождения активных веществ из пористой структуры аэрогелей основной величиной, характеризующей количество введенного вещества A, является массовая доля ω(A). Для кубической сетки с шагом h легко вычислить, что величина ω(A) связана с объемной долей заполнения φ(A) следующим соотношением:
где M(A) – молярная масса вещества A; ρ(SiO2) – плотность кристаллического диоксида кремния; φ(SiO2) – объемная доля диоксида кремния. Таким образом, задавшись определенной массовой долей, по формуле (1) вычисляется доля ячеек, занятых активным веществом. Активное вещество распределяется случайным образом по свободным ячейкам.
Рис. 3. Чередование четной (а) и нечетной (б) решеток на каждой итерации Изложенная последовательность действий позволяет сгенерировать структуру аэрогеля заданной пористости, содержащую в своих порах одиночные молекулы активного вещества. Далее такая структура исследуется в отношении кинетики высвобождения с помощью метода клеточных автоматов с окрестностью Марголуса. Клеточные автоматы с окрестностью Марголуса Клеточные автоматы являются абстрактными динамическими системами с дискретным временем. Моделируемая система разбивается на ячейки, каждая из которых в дискретные моменты t=1,2,… меняет свое состояние в зависимости от состояния соседних ячеек. Число возможных состояний ячеек конечно. Правила перехода, по которым изменяются состояния автомата, могут быть детерминистическими или вероятностными. Сложная динамика системы может быть описана при использовании простых правил перехода. Локальные правила в явном или неявном виде учитывают законы сохранения (массы, импульса, энергии) или некоторые фундаментальные принципы (возрастание энтропии в изолированной системе, принцип максимального действия). Особым классом клеточных автоматов являются такие, правила которых в явном виде учитывают микроскопическую обратимость физических систем. Одним из простых автоматов с таким поведением является клеточный автомат с окрестностью Марголуса. Для наглядности рассмотрим двухмерный вариант такого клеточного автомата. Множество клеток разбивается на множество блоков – конечных, однородных частей (рис. 3а). В простейшем виде блоки имеют размер 2´2. На следующем шаге разбиение меняют так, чтобы возникало некоторое перекрытие блоков на шагах tn-1 и tn (рис. 3б). Именно такую схему называют окрестностью Марголуса. Таким образом, разбиения чередуются, чем достигается однородность пространства и времени. Для всех блоков задается единое правило перехода: на каждом временном шаге блок может поворачиваться по часовой стрелке на π/2, против часовой стрелки на π/2 или оставаться без поворота с вероятностями Pcw, Pccw и Pn соответственно. В простейшем случае вероятности равны 1/3 или Pcw=Pccw=1/2, Pn=0. В работе [2] показано, что в последнем случае динамика поведения такого автомата удовлетворяет уравнению диффузии с коэффициентом диффузии D=1,5. Описанный алгоритм распространен на трехмерный случай и состоит из следующих шагов. 1. Трехмерная сетка разбивается на блоки размерностью 2´2´2 двумя способами – четным и нечетным разбиениями. 2. На текущем временном шаге каждый из блоков четного разбиения поворачивается на π/2 по часовой стрелке, против часовой стрелки или сохраняет свое исходное положение с равной вероятностью (выбирается при помощи генератора случайных чисел). Аналогичная операция проделывается с блоками нечетного разбиения. Блоки, в которых хотя бы одна ячейка оказалась занятой структурой диоксида кремния, не поворачиваются. Тем самым моделируются жесткие стенки пор аэрогеля. Ячейки, содержащие молекулы активного вещества и вышедшие за границу объема структуры, считаются ушедшими в объем растворителя и в дальнейшем не учитываются. 3. Шаги 1, 2 повторяются до тех пор, пока в процессе десорбции из структуры не будет удалено заданное количество молекул вещества или кривая высвобождения перестанет возрастать. Последнее легко проверить статистически. Рассмотренный алгоритм требует для своей реализации существенных вычислительных затрат. Созданная для реализации алгоритма программа для параллельных вычислений реализована на высокопроизводительном компьютере, собранном по технологии CUDA. Такая технология позволяет выполнять программы на графическом процессоре (GPU) видеокарты. В настоящей работе использовался компьютер, состоящий из 4 видеокарт (GeForce GTX 280) с объемом памяти 1 Гб на каждой. Программная реализация алгоритмов выполнена на языке программирования C.
Рис. 4. Исходная плотно упакованная структура (а), перколирующий кластер (б) Рассмотрим структуру программы параллельных вычислений в модели клеточных автоматов. 1. Сгенерированная структура копировалась в память GPU. 2. На каждом шаге для четных и нечетных разбиений производились следующие действия: · каждый блок 2´2´2 рассчитывался в отдельном программном потоке; · потоки объединялись в блоки максимальной размерности 8´8´8 потоков (ограничение в 512 потоков на блок является верхним пределом для существующих архитектур CUDA). Это позволит мультипроцессору GPU при ветвлениях программы выбирать как можно больше параллельно идущих потоков и объединять их для совместного выполнения. Основным же требованием к количеству потоков в блоке является кратность этого числа 32; · количество блоков вычислялось таким образом, чтобы покрыть всю структуру; · в конце шага подсчитывалось количество вещества, находящегося в структуре; · при достижении условия окончания происходил выход из программы. Таким образом, при проектировании архитектуры программы было сведено до минимума количество операций копирования информации между памятью GPU и основной памятью компьютера, на CPU были возложены лишь управляющие действия.
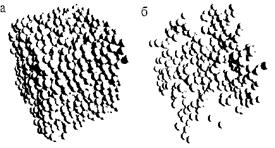
Рис. 5. Кинетика высвобождения активного вещества из пористого тела 500´500´500 нм: 1) ω=90 %; 2) ω=80 %; 3) ω=60 % Результаты моделирования На первом этапе для глобул радиуса r=4 нм и величины перекрывания ψ=0,4 сгенерированы три структуры аэрогелей с различным значением пористости ω=60, 80 и 90 %. На рисунке 4а изображены элементы плотнейшей структуры, на рисунке 4б – структуры с частью удаленных шаров. Структура на рисунке 4б является перколирующей, несмотря на кажущееся отсутствие связности шаров в нижней части рисунка. Это противоречие снимается наличием тороидальных граничных условий. Полученные структуры были перенесены на кубическую сетку размером 529´529´529 с шагом h=1 нм. Правило перехода, моделирующее диффузию, давалось заданием вероятностей поворотов Pcw=Pccw=Pn=1/3. Параметры в формуле (1) равны: M(A)=250 г/моль, φ(SiO2)=2,2 г/мл. На рисунке 5 показана динамика высвобождения активного вещества при разных значениях пористости. Обращает на себя внимание тот факт, что при низкой пористости (60 %) высвобождение происходит быстрее, чем при ω=80 и 90 %, однако абсолютное количество десорбированного вещества мало (не более 1,5 %). По-видимому, это связано с тем, что повороты ячеек практически не происходят, что отвечает случаю сильной адсорбции. При значениях пористости ω=80 и 90 % объемная доля высвобожденного вещества оказывается больше: 20 и 55 % соответственно. Модельное время (число итераций) при практическом моделировании необходимо связать с физическим временем, что достигается сравнением экспериментальной кривой с рассчитанной для какого-либо значения пористости. Рассмотренные модели дают возможность, используя простые правила перехода, описать диффузию в пористых телах. Предложенный алгоритм клеточного автомата с окрестностью Марголуса позволяет проводить параллельные вычисления, что особенно актуально при решении трехмерных задач массо- и теплопереноса и найдет приложение в многочисленных областях физического и химического моделирования. Литература 1. Smirnova I., Suttiruengwong S., Seiler M., Arlt W. Pharmaceutical development and technology, V. 9 (2004), N. 4, pp. 443–452. 2. Малинецкий Г.Г., Степанцов М.Е. Моделирование диффузионных процессов с помощью клеточных автоматов с окрестностью Марголуса. // Журн. вычислит. матем. и матем. физ. – 1998. – Т. 38. – № 6. – С. 1017–1020. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2026 |
Версия для печати Выпуск в формате PDF (3.60Мб) |
| Статья опубликована в выпуске журнала № 1 за 2009 год. [ на стр. 64 ] |
Назад, к списку статей




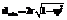

 , (1)
, (1)