Авторитетность издания
Добавить в закладки
Следующий номер на сайте
SPSC: суперкомпилятор на языке Scala
Аннотация:
Abstract:
| Авторы: Романенко С.А. () - , Ключников И.Г. () - | |
| Ключевые слова: функциональное и объектно-ориентированное программирование, scala, специализация программ, суперкомпилятор, суперкомпиляция, метавычисления, анализ и оптимизация программ, преобразования программ |
|
| Keywords: , , , , , , , |
|
| Количество просмотров: 9294 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
Суперкомпиляция [1–3] – метод преобразования программ, предложенный В.Ф. Турчиным в 70-х годах прошлого века. Несмотря на то, что суперкомпиляции посвящено немало литературы, практически везде алгоритмы суперкомпиляции описаны либо неполностью и фрагментарно, либо чрезмерно абстрактно (например, в виде каких-то спецификаций или правил вывода). Поэтому трудно проверить работоспособность предлагаемых методов и алгоритмов. Если информация неполная, читателю предлагается самому восстановить недостающие части (и нет гарантии, что он сделает это именно так, как подразумевал автор статьи). Если материал представлен слишком абстрактно, превращение его в работающие программы – сложный и неоднозначный процесс. Цель данной статьи – представить полный текст простого, но работоспособного суперкомпилятора. Это даст возможность программисту-практику ознакомиться с суперкомпиляцией, представленной на понятном ему языке – в виде конкретных программ. Причем при желании можно проверить представленные алгоритмы на деле, взяв текст суперкомпилятора прямо из статьи. В качестве языка реализации суперкомпилятора используется язык Scala [4]. Это объясняется тем, что для описания одних аспектов суперкомпиляции хорошо подходит функциональный стиль программирования, для описания других – объектно-ориентированный, а особенностью языка Scala является то, что в нем удалось органично соединить возможности как функционального, так и объектно-ориентированного программирования. При этом Scala – вполне практичный язык программирования: все, что может быть написано на языке Java, легко может быть записано и на языке Scala (причем программа при этом становится короче). В настоящее время имеется реализация языка Scala, основанная на компиляции в виртуальный код JVM (Java Virtual Machine) и обеспечивающая возможность создавать программы, различные части которых написаны на Scala и на Java. В статье рассматривается простейший суперкомпилятор SPSC для ленивого функционального языка первого порядка [5]. Рассмотрим программу на простом функциональном языке, конкатенирующую списки: gApp(Nil(), vs)=vs; gApp(Cons(u, us), vs)=Cons(u, gApp(us, vs)); Допустим, требуется получить результат конкатенации трех списков. Это можно сделать, вычислив выражение gApp(gApp(xs, ys), zs). Однако при этом элементы списка xs будут анализироваться два раза (сначала внутренним вызовом gApp, а потом наружным). С помощью суперкомпиляции можно получить более эффективную программу. Интерпретируем выражение (конфигурацию) gApp(gApp(xs, ys), zs). Сначала раскроем внутренний вызов gApp(xs, ys). Поскольку gApp проверяет, какой вид имеет ее первый аргумент – Nil() или Cons(u, us), рассмотрим два случая суперкомпиляции, то есть расщепим конфигурацию (рис. 1). Правую конфигурацию теперь можно однозначно развернуть, заменить наружный вызов gApp (рис. 2). Новое выражение содержит конструктор на верхнем уровне, с которым в данный момент ничего полезного сделать нельзя. Поэтому переходим к символическому вычислению аргументов конструктора (рис. 3). Конфигурация в нижнем правом узле получившегося дерева (рис. 3) совпадает с конфигурацией в корне дерева (с точностью до переименования переменных). Понятно, что нет смысла анализировать ее второй раз. Оставив gApp(gApp(us, ys), zs), символически вычислим gApp(ys, zs), получив через два шага решение, изображенное на рисунке 4. Построение дерева конфигураций завершено: каждый лист дерева содержит ранее встречавшуюся конфигурацию (с точностью до переименования переменных), либо переменную, либо нуль-арный конструктор. Можно сказать, что построенное таким образом дерево представляет все возможные пути вычисления выражения, находящегося в его корне. Ветвления в дереве получаются из разбора возможных значений переменных.
gApp1(Nil(), y, z)=gApp2(y, z); gApp1(Cons(v1, v2), y, z)=Cons(v1, gApp1(v2, y, z)); gApp2(Nil(), z)=z; gApp2(Cons(v3, v4), z)=Cons(v3, gApp2(v4, z)); Видно, что при вычислении выражения gApp1(xs, ys, zs) элементы списка xs анализируются только один раз, в то время как при вычислении исходного выражения gApp(gApp(xs, ys), zs) они анализировались дважды.
Входной язык Входным языком суперкомпилятора SPSC, рассмотренного в статье, является SLL – ленивый функциональный язык первого порядка. В языке SLL используется перечислимое множество символов для представления переменных x∈X, конструкторов c∈C и имен функций f∈F и g∈G. Все символы имеют фиксированную арность. SLL-программы обрабатывают данные, представляющие собой конечные деревья, построенные с помощью конструкторов. Синтаксис языка SLL состоит из набора определений функций. Причем функции делятся на два класса: f-функции и g-функции. Определение g-функции состоит из одного или нескольких правил, при этом в каждом правиле присутствует образец, с помощью которого анализируется структура первого аргумента. Определение f-функции состоит из одного правила, в котором все аргументы являются переменными. Синтаксис языка: p ::= d1 .. dn (программа) d ::= f(x1,...,xn) = e; (f-функция) | g(q1, x1,...,xn) = e1; (g-функция) ... g(qm, x1,...,xn) = em e ::= x (переменная) | c(e1,...,en) (конструктор) | f(e1,...,en) (вызов f-функции) | g(e1,...,en) (вызов g-функции) q ::= c(x1,...,xn) (образец) Для упрощения некоторых (несущественных) технических деталей в суперкомпиляторе потребуем, чтобы имена переменных начинались со строчной буквы, конструкторов – с прописной, а f- и g-функций – с f и g соответственно. Семантика вычислений на языке SLL ленивая. Поэтому язык SLL является в сущности небольшим подмножеством языка Haskell. В приведенной ранее программе определены два конструктора для представления списков – Nil и Cons, g-функция gApp конкатенирует два списка. Абстрактный синтаксис Представим реализацию абстрактного синтаксиса SLL на языке Scala (начало очень похоже на Java, но есть некоторые существенные отличия). Сначала объявляется абстрактный класс Term, который используется для представления выражения языка SLL. В теле класса определены два абстрактных метода: defs и args, которые абстрактными становятся автоматически, так как у них отсутствует реализация. abstract class Term{def name: String; def args: List[Term]} case class Ctr(name: String, args: List[Term]) extends Term case class FCall(name: String, args: List[Term]) extends Term case class GCall(name: String, args: List[Term]) extends Term case class Var(name: String) extends Term {val args = null} case class Let(term: Term, bs: List[(Var, Term)]) extends Term {val (name, args) = (null, Nil)} case class Pattern(name: String, args: List[Var]) case class FFun(name: String, args: List[Var], term: Term) case class GFun(name: String, p: Pattern, args: List[Var], term: Term) case class Program(defs: List[Either[FFun, GFun]]){ def f(f: String) = (List.lefts(defs) find {f == _.name}).get def gs(g: String) = List.rights(defs) filter {g == _.name} def g(g: String, p: String) = (gs(g) find {p == _.p.name}).get } Далее объявляется класс Ctr, который изображает данные языка SLL и является подклассом класса Term. В языке Scala каждый класс обязан иметь основной (primary) конструктор, аргументы которого указываются сразу после имени класса, причем аргументы основного конструктора превращаются в поля класса. Конструктор Ctr имеет аргумент name (типа строка), поэтому name является членом класса Ctr. Использование ключевого слова сase означает, что экземпляры класса можно сопоставлять с образцом. Например, если значением переменной t является объект класса Ctr, то напечатается значение поля name этого объекта, иначе ничего не произойдет: t match { case Ctr(name, args) => print(name) case _ => } В Scala значения (переменные, поля) бывают модифицируемые и немодифицируемые. Первые объявляются с помощью ключевого слова var, вторые – val. Методы объявляются с помощью ключевого слова def. Класс Ctr имеет также поле args – список аргументов конструктора, представленных объектами класса Term. Тип списка arg записывается как List[Term]. То есть квадратные скобки в Scala не обозначают обращение к элементам массива, а используются для записи аргументов у конструкторов типов. (В Java для этого же применяются угловые скобки.) Тело класса пустое, поэтому оно (в отличие от Java) может быть опущено. В определении метода name в классе Term отсутствует список параметров, в результате чего вызов метода name внешне выглядит как обращение к полю класса. Это позволяет в Scala-программах заменять реализацию свойств объекта (поле на метод или наоборот), не затрагивая части программы, использующие метод. В подклассах Ctr, FCall, GCall есть поля name и args, и это приводит к тому, что автоматически появляются реализации методов name и args, объявленных в базовом классе Term. В классе Program, помимо списка определений defs (определен в конструкторе), используются три метода – f, g и gs, где f выдает f-функцию по имени; g выдает g-функцию по имени и образцу; gs выдает список всех определений g-функции с данным именем. При определении абстрактного синтаксиса языка SLL мы придерживались функционального стиля: все синтаксические объекты являются неизменяемыми значениями. Let-выражение, не соответствующее какой-либо конструкции в языке SLL, может порождаться в процессе работы суперкомпилятора. Операции над выражениями Подстановкой называется набор пар вида (v, t), где v – переменная; t – терм. В терминах Scala для представления подстановок удобно использовать словари типа (Map[Var, Term]), у которых ключом является переменная, а значением – выражение. Процесс применения подстановки к терму интуитивно понятен: находим в терме все переменные из области определения подстановки и заменяем их на соответствующие термы, что и реализовано в методе sub. Метод findSub находит (если это возможно) для двух выражений t1 и t2 подстановку m, такую что sub(t1, m)=t2. Идея заключается в том, что мы начинаем с пустой подстановки и помещаем в нее новые значения, обходя оба выражения одновременно методом walk. Метод inst тестирует, является ли второе выражение частным случаем первого. Метод vars возвращает список использованных переменных в данном терме. Здесь использованы высокоуровневые методы коллекций Scala: map, /: (синтаксический сахар для foldLeft), filter, forall, локальные частичные функции для case-выражений. Также удобна синтаксическая конструкция для «закарривания» функций: sub(_, map) эквивалентно (x) => sub(x, map): object Algebra { def sub(term: Term, map: Map[Var, Term]): Term = term match { case v: Var => map.getOrElse(v, v) case Ctr(n, vs) => Ctr(n, vs.map(sub(_, map))) case FCall(n, vs) => FCall(n, vs.map(sub(_, map))) case GCall(n, vs) => GCall(n, vs.map(sub(_, map))) } def inst(t1: Term, t2: Term) = findSub(t1, t2) != null def findSub(t1: Term, t2: Term) = { val map = scala.collection.mutable.Map[Var, Term]() def walk(t1: Term, t2: Term): Boolean = t1 match { case v: Var => map.getOrElse(v, t2) == (map+(v -> t2))(v) case _ => t1.getClass == t2.getClass && t1.name == t2.name && List.forall2(t1.args, t2.args)(walk) } if (walk(t1, t2)) Map(map.toSeq:_*).filter{case (k, v) => k != v} else null } def vars(t: Term): List[Var] = t match { case v: Var => (List(v)) case _ => (List[Var]() /: t.args) {_ union vars(_)} } } Дерево процесса Интерпретатор для языка SLL может рассматриваться как некая машина, упрощающая шаг за шагом заданный терм в соответствии с некоторыми правилами (семантикой языка). Отметим, что обычный интерпретатор способен упрощать только термы, не содержащие переменных, причем на каждом шаге редукций правило, которое необходимо применить, определяется однозначно. Вычисление заканчивается, когда текущий терм не содержит в себе вызовов функций. В случае суперкомпиляции преобразуемые термы (конфигурации) могут содержать переменные. Из-за этого возникают ситуации, когда очередное преобразование терма нельзя выполнить однозначно и требуется разбор случаев. Если программа написана на языке SLL, нельзя однозначно упростить вызов g-функции, первым аргументом которого является переменная. Требуется рассмотреть различные образцы из определения g-функции, расщепить текущую конфигурацию и «раскручивать» полученные конфигурации дальше. В результате символических вычислений (иначе – метавычислений [5]) строится дерево процесса – ориентированное дерево, в корне которого находится начальная конфигурация. В прямых потомках узла находятся конфигурации, получающиеся за один шаг метавычислений. Если произошло расщепление конфигурации, то дуге, связывающей родительский узел с дочерним, приписывается сужение – выбранный образец. Для описания дерева процесса используются 3 класса. Node – узел дерева, ссылающийся на входящие и выходящие дуги графа и на содержащееся в нем выражение. Edge – дуга, связывающая родителя и потомка. Поле pat описывает сужение (выбранный образец при расщеплении конфигурации). Tree – дерево узлов. Класс Tree имеет несколько вспомогательных методов: leaves выдает список листьев дерева (узлов без потомков), replace заменяет выражение в данном узле и удаляет поддерево, addChildren конструирует из выражений узлы дерева и добавляет их к данному узлу: class Edge(val in: Node, var out: Node, val pat: Pattern) case class Node(expr: Term, in: Edge, var outs: List[Edge], var fnode: Node) { def ancestors: List[Node] = if (in == null) Nil else in.in :: in.in.ancestors def leaves: List[Node] = if (outs.isEmpty) List(this) else children.flatMap(_.leaves) def children : List[Node] = outs map {_.out} def isProcessed: Boolean = expr match { case Ctr(_, Nil) => true case v: Var => true case _ => fnode != null } } class Tree(var root: Node) { def leaves = root.leaves def replace(node: Node, exp: Term) = node.in.out = Node(exp, node.in, Nil, null) def addChildren(node: Node, children: List[(Term, Pattern)]) = node.outs = for ((term, p) <- children) yield { val edge = new Edge(node, null, p) edge.out = Node(term, edge, Nil, null) edge } } Cуперкомпилятор В общем случае дерево процесса, построенное в результате метавычислений, будет бесконечным. В основе суперкомпиляции лежит идея, что при построении дерева процесса будут встречаться конфигурации, похожие на ранее встречавшиеся. Например, conf2 – это conf1 с точностью до переименования переменных. Значит, в дальнейшем conf2 будет развиваться так же, как и conf1 – ее предок, и можно не строить поддерево для conf2, а зациклить conf2 на conf1. Узел с conf1 называется базовым узлом, с conf2 – повторным. Может оказаться, что существует подстановка s, которая, будучи примененной к ранее встретившейся конфигурации conf1, даст текущую конфигурацию conf2. В этом случае говорят, что conf2 – частный случай conf1, а значит, conf2 далее будет развиваться, как conf1 (с учетом найденной подстановки s): опять можно зациклить, построив соответствующие деревья для термов из s (для этого используется let-выражение). Таким образом, получается частичное дерево процесса. Из такого дерева можно сгенерировать программу, которая будет эквивалентна исходной, причем некоторые «излишки» исходной программы могут быть устранены. В случае суперкомпиляции метавычисления называют прогонкой [3–5]. Опишем алгоритм построения частичного дерева процесса. Для представления зацикливания используем поле fnode в классе Node, для представления выбранного при расщеплении конфигураций образца – поле pat класса Edge. Выражение называется тривиальным, если оно является конструктором, переменной или let-выражением. Узел называется обработанным, если он ссылается на функциональный узел либо на узел с переменной или нуль-арным конструктором. Построение частичного дерева процесса начинается с помещения в корень дерева исходного выражения. Затем (пока есть хотя бы один необработанный лист b): · если лист тривиальный, прогоняем выражение в этом узле; · если среди предков b есть узел а, такой, что выражения в этих узлах совпадают с точностью до переименования, делаем узел a базовым узлом b; · если среди предков b есть узел а, такой, что выражение в b является экземпляром выражения в а, то заменяем выражение в b на let-выражение, где bs – найденная подстановка, а к b в качестве потомков прикрепляем значения подстановок; · в противном случае применяем прогонку. Особенностью прогонки является прогонка вызова g-функции с переменной в качестве первого (образцового) аргумента. В этом случае конфигурация расщепляется соответственно образцам g-функции. При описании прогонки помогают сложные образцы вроде case GCall(name, Ctr(cname, cargs) :: args). Кроме того, Scala дает изобразительные средства для использования методов (и конструкторов) в качестве бинарных операторов, например :: является конструктором списков: :: (head, tail) эквивалентно head :: tail. import Algebra._ class SuperCompiler(p: Program){ def driveExp(expr: Term): List[(Term, Pattern)]=expr match { case gCall @ GCall(n, (v : Var) :: _) => for (g <- p.gs(n); val pat = fPat(g.p); val ctr = Ctr(pat.name, pat.args)) yield (driveExp(sub(gCall, Map(v -> ctr)))(0)._1, pat) case Ctr(name, args) => args.map((_,null)) case FCall(n, vs) => List((sub(p.f(n).term, Map()++p.f(n).args.zip(vs)), null)) case GCall(name, Ctr(cname, cargs) :: vs) => val g = p.g(name, cname) List((sub(g.term, Map((g.p.args:::g.args) zip (cargs ::: vs): _*)), null)) case GCall(n, f :: vs) => driveExp(f) map {case (v, p) => (GCall(n, v :: vs), p)} case Let(term, bs) => (term, null) :: bs.map {case (_, x) => (x, null)} } def buildProcessTree(e: Term) = { val t = new Tree(Node(e, null, Nil, null)) def split(a: Node, b: Node) = t.replace(a, Let(a.expr, findSub(a.expr, b.expr).toList)) def step(b: Node) = if (trivial(b.expr)) t.addChildren(b, driveExp(b.expr)) else b.ancestors.find(a => inst(a.expr, b.expr)) match { case Some(a) => if (inst(b.expr, a.expr)) b.fnode = a else split(b, a) case None => t.addChildren(b, driveExp(b.expr)) } while (t.leaves.exists{!_.isProcessed}) step(t.leaves.find(!_.isProcessed).get) t } def trivial(t: Term)=t match{case _:FCall=>false;case _:GCall=>false;case _=>true} private var i = 0 private def fPat(p: Pattern)=Pattern(p.name, p.args.map {_ => i+=1; Var("v" + i)}) } Следует отметить, что при описании суперкомпилятора и частичного дерева процесса использовались как функциональные (метод driveExp), так и объектные средства: Scala позволяет смешивать различные парадигмы программирования. Написать суперкомпилятор в чисто функциональном стиле, конечно, можно, но получившийся при этом код был бы заметно более громоздким. Генератор остаточной программы Принцип генерации остаточной программы из частичного дерева процесса прост: каждое зацикливание порождает рекурсивную функцию, каждое расщепление конфигурации порождает функцию. При генерации остаточной программы из дерева суперкомпиляции это дерево обходится сверху вниз методом walk. При посещении базового узла генерируется определение функции: если в этом узле произошло расщепление конфигурации, генерируется g-функция, в противном случае – f-функция. Определение функции состоит из сигнатуры (названия и порядка аргументов) и тела функции. Арность функции определяется исходя из количества переменных в данной конфигурации. При обходе базового узла генерируется сигнатура. При обходе узла, ссылающегося на функциональный узел, генерируется рекурсивный вызов функции, определенной в базовом узле. При обходе узла с конструктором генерируется конструктор, аргументы которого являются результатом обхода дочерних узлов. В остальных случаях итогом является результат обхода дочернего узла (транзитный шаг). Отметим, что при определении функций генерируются синтаксически корректные имена: f-функции начинаются с f и g-функции – с g. Генератор остаточной программы выдает пару – новое выражение и список определений. import Algebra._ class ResidualProgramGenerator(val tree: Tree) { var (sigs, defs) = (Map[Node, (String, List[Var])](),List[Either[FFun, GFun]]()) lazy val result = (walk(tree.root), Program(defs)) private def walk(n: Node): Term = if (n.fnode == null) n.expr match { case v: Var => v case Ctr(name,args) => Ctr(name, n.children.map(walk)) case Let(_,b) => sub(walk(n.children(0)), Map()++b.map{_._1}.zip(n.children.tail map walk)) case c: Term => if (n.outs(0).pat != null) { sigs += (n -> ("g" + c.name.drop(1) + sigs.size, vars(c))) for (e <- n.outs) defs = Right(GFun(sigs(n)._1, e.pat, vars(c).tail, walk(e.out)))::defs GCall(sigs(n)._1, vars(c)) } else if (tree.leaves.exists(_.fnode == n)) { sigs += (n -> ("f" + c.name.drop(1) + sigs.size, vars(c))) defs = Left(FFun(sigs(n)._1, sigs(n)._2, walk(n.children(0)))) :: defs FCall(sigs(n)._1, vars(c)) } else walk(n.children(0)) } else if (n.fnode.outs(0).pat == null) sub(Function.tupled(FCall)(sigs(n.fnode)), findSub(n.fnode.expr, n.expr)) else sub(Function.tupled(GCall)(sigs(n.fnode)), findSub(n.fnode.expr, n.expr)) } Парсер входного языка Опишем парсер, который преобразует SLL-программы, представленные в конкретном синтаксисе (в виде последовательности литер), в SLL-программы, представленные в абстрактном синтаксисе (в виде деревьев). Это позволяет продемонстрировать некоторые интересные возможности языка Scala. Стандартная библиотека Scala включает в себя пакет для написания парсеров в комбинаторном стиле. Идея комбинаторного парсирования заключается в построении сложных парсеров из более простых путем их объединения с помощью комбинаторов, то есть функций, принимающих парсеры в качестве аргументов и возвращающих новые парсеры. Благодаря тому, что Scala позволяет использовать объектно-ориентированные средства, парсеры естественным образом реализуются в виде классов. А именно, каждый парсер является подклассом абстрактного класса: abstract class Parser[+T] extends (Input => ParseResult[T]) {...} При этом класс Parser является функцией, поскольку имеет функциональный тип Input => ParseResult[T]. Здесь уместно напомнить, что функции в Scala являются объектами, то есть могут не только применяться к аргументам, но и содержать дополнительные поля и методы. Input – тип того, что подается парсеру на вход: в нашем случае это поток токенов (поток получается благодаря стандартному лексеру). T – тип того, что в итоге получается на выходе, в данном случае необходимо из текста получить объекты дерева абстрактного синтаксиса языка SLL, а именно программу. ParseResult[T] – абстрактный класс, подклассами которого являются успех (Success[T]) и неудача (Failure). Как было отмечено, парсер – это одновременно функция и объект с соответствующими методами. Стандартная реализация (StandardTokenParsers) предоставляет элементарные парсеры, разбивающие текст на строки – идентификаторы, ключевые слова, разделители и пр. Таким образом, примитивные стандартные парсеры в результате потока токенов выдают список строк, а дерево абстрактного синтаксиса можно построить с помощью комбинаторов – методов, получающих парсеры в качестве аргументов и выдающих парсеры. Стандартный класс Parsers определяет необходимые базовые комбинаторы: · x | y – «или» (если x успешно завершается, то выдает результат работы x, если y успешно завершается, то выдает результат работы y, иначе выдает ошибку); · x ~ y – «и затем» (выдает результат работы x и y в виде двухэлементного кортежа, если x, а затем и y успешно завершаются); · x+ – многократное повторение (от единицы), результат – список; · x ^^ f – применение к результату работы x функции f; · x ^? f – применение к результату работы x частичной функции f (успешен, если f определена на результате работы x); · x ~> y – аналогичен ~, возвращает только результат работы y; · x <~ y – аналогичен ~, возвращает только результат работы x; · repsep(x, del) – повтор с разделителями del(строка), результат – список из результатов работы x. Поскольку Scala позволяет использовать для названий классов и методов практически любые строки, реализация парсера на скале очень близка к BNF-грамматике языка, а названия комбинаторов передают их смысл. Перейдем к модулю парсинга языка SLL. В первой строке определим разделители, далее – парсер fid, который соответствует идентификатору, начинающемуся с буквы f. Здесь воспользуемся стандартным парсером ident, распознающим последовательность букв и цифр, начинающуюся с буквы. С помощью комбинатора ^? получим новый парсер. Уместно вспомнить, что последовательность case-выражений – это не просто функция, а частичная функция, определенная на перечисленных образцах. Аналогично конструируются парсеры gid, uid и lid (идентификатор, начинающийся с g, идентификатор, начинающийся со строчной буквы, и идентификатор, начинающийся с прописной буквы, соответственно). Используются case-выражения с ограничениями – case-выражение срабатывает, если срабатывает образец и выполняется записанное после него условие. Следующие парсеры почти очевидны – парсер vrb принимает строку и выдает объект абстрактного синтаксиса – переменную. Обратим внимание, что конструктор может рассматриваться как функция соответствующей арности, то есть для унарного конструктора выражение Ctx эквивалентно (x => Ctx x). import scala.util.parsing.combinator.ImplicitConversions import scala.util.parsing.combinator.syntactical.StandardTokenParsers import scala.util.parsing.input.{CharSequenceReader => Reader} object SParsers extends StandardTokenParsers with ImplicitConversions { lexical.delimiters += ("(", ")", ",", "=", ";") def defs = (fFun ^^ {Left(_)} | gFun ^^ {Right(_)})+ def term: Parser[Term] = fcall | gcall | ctr | vrb def uid = ident ^? {case id if id.charAt(0).isUpperCase => id} def lid = ident ^? {case id if id.charAt(0).isLowerCase => id} def fid = ident ^? {case id if id.charAt(0) == 'f' => id} def gid = ident ^? {case id if id.charAt(0) == 'g' => id} def vrb = lid ^^ Var def ptr = uid ~ ("(" ~> repsep(vrb, ",") <~ ")") ^^ Pattern def fFun = fid ~ ("(" ~> repsep(vrb, ",") <~ ")") ~ ("=" ~> term <~ ";") ^^ FFun def gFun=gid ("(" ~> ptr) ~ ((("," ~> vrb)*) <~ ")") ~ ("=" ~>term <~ ";")^^GFun def ctr = uid ~ ("(" ~> repsep(term, ",") <~ ")") ^^ Ctr def fcall = fid ~ ("(" ~> repsep(term, ",") <~ ")") ^^ FCall def gcall = gid ~ ("(" ~> repsep(term, ",") <~ ")") ^^ GCall def parseProgram(s: String)=Program(defs(new lexical.Scanner(new Reader(s))).get) def parseTerm(s: String) = term(new lexical.Scanner(new Reader(s))).get } Главные методы, которыми следует пользоваться: 1. parseProgram: String => Program – преобразует (корректное) текстовое представление программы в саму программу; 2. parseTerm: String => Term – преобразует (корректное) текстовое представление терма в дерево абстрактного синтаксиса. Пример Рассмотрим описанную программу, в которой выражение gApp(gApp(x, y), z) конкатенирует 3 списка, однако делает это неэффективно: получается, что список x анализируется на предмет соответствия образцу 2 раза. Первый раз – при вызове gApp(x, y). Этот вызов создает промежуточную структуру данных – список, который затем будет проанализирован еще раз. Список x анализируется еще раз при обходе промежуточного списка. Суперкомпилятор для этой программы на языке SLL вызывается следующим образом: val programText = """ gApp(Nil(), vs1) = vs1; gApp(Cons(u, us), vs) = Cons(u, gApp(us, vs)); """ val p = SParsers.parseProgram(programText) val sc = new SuperCompiler(p) val pt = sc.buildProcessTree(SParsers.parseTerm("gApp(gApp(x, y), z)")) val (expr, p1) = new ResidualProgramGenerator(pt).result println(expr) println(p1) В результате на консоли выведутся новое выражение и остаточная программа, будет видно, что список x анализируется один раз и что остаточная программа содержит первоначальное определение конкатенации (gApp1) и специализированное (gApp0) – для конкатенации трех списков. gApp0(x, y, z) gApp0(Cons(v1, v2), y, z) = Cons(v1, gApp0(v2, y, z)); gApp0(Nil(), y, z) = gApp1(y, z); gApp1(Cons(v3, v4), z) = Cons(v3, gApp1(v4, z)); gApp1(Nil(), z) = z; В этой статье мы постарались описать простейший суперкомпилятор для ленивого функционального языка первого порядка. При этом преследовалась цель представить полный код суперкомпилятора. Однако построение частичного дерева процесса так, как это описано в статье, не всегда завершается. Ситуации, когда дерево конфигурации начинает опасно разрастаться, определяются с помощью специального критерия, называемого в суперкомпиляции свистком. В этом случае одна из конфигураций (которая приводит к бесконечному росту) обобщается – некоторые части конфигураций заменяются на переменные. Суперкомпиляция со свистком и обобщением завершается всегда. Подробнее о более совершенной версии суперкомпилятора можно ознакомиться на сайте проекта в Интернете (http://spsc.googlecode.com). Литература 1. Turchin V.F. The Language Refal: The Theory of Compilation and Metasystem Analysis. Department of Computer Science, Courant Institute of Mathematical Sciences, New York University, 1980. 2. Turchin V.F. The concept of a supercompiler. ACM Transactions on Programming Languages and Systems (TOPLAS), 1986. № 8 (3). pp. 292–325. 3. Абрамов С.М., Парменова Л.В. Метавычисления и их применение. Суперкомпиляция: учебник. – Переславль-Залесский: Изд-во «Университет города Переславля имени А.К. Айламазяна», 2006. 76 с. 4. Odersky M., Spoon L. and Venners B. Programming in Scala: A Comprehensive Step-by-step Guide. Artima Inc. 2008. 5. Sørensen M.H. Convergence of program transformers in the metric space of trees. In Mathematics of Program Construction. Vol. 1422 of Lecture Notes in Computer Science. Springer, 1998. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2252 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Назад, к списку статей



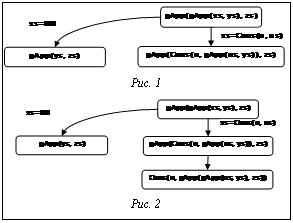 Чтобы построить программу из полученного дерева конфигураций, мы, условно говоря, генерируем для каждого узла alpha с дочерним узлом beta определение функции, где левая и правая части определения выводятся из alpha и beta соответственно. В этом примере переименуем выражение gApp(gApp(xs, ys), zs) в gApp1(xs, ys, zs) и получим следующую остаточную программу:
Чтобы построить программу из полученного дерева конфигураций, мы, условно говоря, генерируем для каждого узла alpha с дочерним узлом beta определение функции, где левая и правая части определения выводятся из alpha и beta соответственно. В этом примере переименуем выражение gApp(gApp(xs, ys), zs) в gApp1(xs, ys, zs) и получим следующую остаточную программу: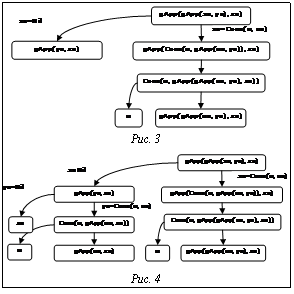 Преобразования проходили в три этапа: символические вычисления, поиск закономерностей и построение остаточной программы, причем первые два этапа перемежались. На первом этапе была развернута конфигурация с добавлением узлов к дереву конфигураций. На втором этапе необходимо было следить за тем, чтобы конфигурации, совпадающие (с точностью до переименования переменных) с ранее обработанными конфигурациями, не развертывались далее. Это продолжалось до тех пор, пока дерево не становилось «завершенным». На последнем этапе была сгенерирована программа из завершенного дерева конфигураций.
Преобразования проходили в три этапа: символические вычисления, поиск закономерностей и построение остаточной программы, причем первые два этапа перемежались. На первом этапе была развернута конфигурация с добавлением узлов к дереву конфигураций. На втором этапе необходимо было следить за тем, чтобы конфигурации, совпадающие (с точностью до переименования переменных) с ранее обработанными конфигурациями, не развертывались далее. Это продолжалось до тех пор, пока дерево не становилось «завершенным». На последнем этапе была сгенерирована программа из завершенного дерева конфигураций.