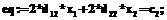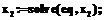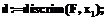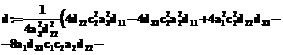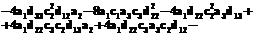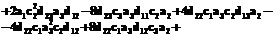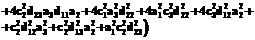Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная поддержка построения области реализуемости термодинамических систем
Аннотация:
Abstract:
| Авторы: Цирлин А.М. () - , Григоревский И.Н. () - | |
| Ключевые слова: тепловая машина, диссипация, программное обеспечение, область реализуемости, системы, необратимая термодинамика |
|
| Keywords: , , the software, , systems, |
|
| Всего комментариев: 1 Количество просмотров: 11022 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
Значительную часть технологических процессов можно охарактеризовать термодинамическими закономерностями. Тепловые и холодильные машины, процессы разделения, сушки, кристаллизации, химические реакторы и другое характеризуются такими переменными, как внутренняя энергия, концентрация тех или иных компонент, температура и энтропия. Параметры входных и выходных потоков в таких системах связаны между собой уравнениями энергетического, материального и энтропийного балансов [1, 2]. Для открытой стационарной системы эти уравнения имеют вид:
где В оптимизационной термодинамике [3] решают задачу о такой организации процесса, при которой для тех или иных ограничений производство энтропии достигает своей нижней границы smin. Для любых условий s³smin, а значит, при подстановке в уравнения (1) smin эти уравнения выделяют в пространстве потоков границу области, которую будем называть областью реализуемых значений параметров системы, или областью реализуемости. Если интенсивность стремится к нулю или коэффициенты тепло- и массопереноса сколь угодно велики, то smin=0 и граница области реализуемости соответствует обратимым процессам. При этом ее граница всегда линейна. Если интенсивность одного или нескольких потоков задана, smin³0 и область реализуемости сужается. Однако может измениться и ее качественный характер, так как функция smin нелинейно зависит от интенсивности потоков. Общие особенности границы области реализуемости Области реализуемости термодинамических систем с ненулевой производительностью (интенсивностью целевого потока) и ограниченными размерами имеют ограниченные коэффициенты переноса. Говорить об общих особенностях можно потому, что множество реализуемости в пространстве потоков вещества и энергии определяется уравнением энтропийного баланса, в которое с постоянными коэффициентами входят потоки энтропии на входе и выходе системы, линейно зависящие от потоков вещества и энергии. Минимально возможное производство энтропии в системе smin(g, p, q), которое является положительно-определенной, строго выпуклой вниз функцией потоков вещества и энергии, зависит от коэффициентов переноса и кинетики химических реакций, стремится к нулю при интенсивности потоков, стремящейся к нулю. Во многих случаях кинетика такова, что потоки пропорциональны движущим силам (законы теплопереноса Фурье, массоперенос, пропорциональный разнице химических потенциалов, и пр.), а в окрестности равновесия это всегда так. В таком случае производство энтропии является положительно-определенной квадратичной формой. При этом потоки связаны друг с другом уравнениями энергетического и материального балансов (см. формулу (1)). Предположим, что число компонентов во входных и выходных потоках равно n. Тогда общее число уравнений (1) равно n+2, так как к уравнениям материального баланса добавлены балансы по энергии и энтропии. Число переменных (потоки вещества и энергии на входе и на выходе системы) обычно гораздо больше, часть из них может быть фиксированной. Для исследования общих особенностей области реализуемости обозначим материальные и энергетические потоки через xi. Выделим целевой поток, характеризующий возможности системы (мощность тепловой машины, хладопроизводительность обратного цикла, расход разделяемой смеси и пр.), и обозначим его через x1, а поток затрат, который может быть одним из входящих в балансовые соотношения или линейной комбинацией xi, обозначим через x2. Минимальное производство энтропии представляет собой квадратичную функцию потоков, если они пропорциональны движущим силам, в противном случае оно может быть аппроксимировано в таком виде. Перепишем уравнения (1) в общей, канонической форме:
Границе области реализуемости соответствует замена в последнем соотношении знака неравенства на знак равенства. Из системы линейных уравнений для невырожденного случая можно исключить n+1 переменных (будем исключать переменные с большими значениями индексов) и подставить в условие энтропийного баланса. Последнее для точек границы области реализуемости примет форму
При этом smin(x) зависит только от переменных, оставшихся после исключения, но, как и ранее, представляет собой выпуклую вниз положительно-определенную квадратичную форму этих переменных. Построим область реализуемости в плоскости с координатами x1 и x2, считая, что значения всех остальных переменных, оставшихся после исключения переменных с большими значениями индексов, фиксированы. В случае отсутствия потоков вещества этих оставшихся переменных может и не быть. Общие свойства границы области реализуемости следующие. · При обращении всех потоков, кроме целевого, в нуль x1 тоже равен нулю, так что граница области проходит через начало координат. · Производная
· В точке максимума целевого потока (если этот максимум существует) наклон границы области реализуемости равен нулю. Условие максимума целевого потока совместно с уравнением границы области реализуемости определяет предельное значение
Если система (5) не имеет действительных корней, то область реализуемости не ограничена сверху (рис. 1а), в противном случае область реализуемости имеет иную форму (рис. 1б), при этом величина целевого потока ограничена значением · Область реализуемости выпукла вверх в силу свойств функции smin(x). Область реализуемости для s³0 обозначим D0 (ее граница соответствует обратимым процессам), а для случая s³smin – Рассмотрим тепловую машину, состоящую из горячего резервуара с температурой Отобразим термодинамические балансы через исходные переменные:
Введем обозначения:
Для определения границы области реализуемости неравенство в (8) заменим на равенство. Из формулы (7) выразим x3 через x1 и x2 и подставим в (8). Получим для границы области реализуемости квадратичное выражение вида F(x1, x2)=0 с двумя переменными. Функция найдена с помощью пакета Maple (см. уравнение (24)). Чтобы найти точку экстремума границы области реализуемости, воспользуемся уравнением (5), которое линейно относительно x1 и x2. Из решения этого уравнения совместно с условием
определяем
Это уравнение имеет действительный корень, если его дискриминант D неотрицателен. Условие неотрицательности D, выраженное через коэффициенты системы, записанной в канонической форме, получено с использованием пакета и дано в задаче 4. Если это условие выполнено, область реализуемости имеет форму, как на рисунке 1б. Если дискриминант отрицателен, область реализуемости имеет вид, как на рисунке 1а. При известных коэффициентах канонической формы можно вычислить значение дискриминанта и определить вид области достижимости. Пример расчета Продолжим рассмотрение примера с тепловой машиной. После исключения x3 запишем систему в виде (2):
Таким образом, коэффициенты Обратимый КПД равен КПД Карно и не зависит от законов теплообмена. Для построения границы области реализуемости воспользуемся решением задачи о минимальной диссипации в цикле тепловой машины [4], приняв заданными коэффициенты теплообмена рабочего тела с источниками
Здесь T1 и T2 – температуры рабочего тела при контакте с источниками. Отметим, что для принятой формы закона теплообмена (его называют ньютоновским) поток непропорционален движущей силе, равной разности обратных значений температур, поэтому производство энтропии не является квадратной функцией потока и нахождение коэффициентов требует его аппроксимации квадратичной формой. Для этих ньютоновских законов теплообмена задача о минимальной диссипации решена в [4], в которой найден предельный КПД тепловой машины заданной мощности:
где В свою очередь, Ясно, что smin=0 при x1=0 и smin>0 при x1>0, причем при малом значении мощности зависимость s(x1) квадратична. Чтобы воспользоваться условием (5), необходимо найти значение коэффициента d22. Для этого выразим smin через x2. Так как
и smin перепишется в виде
Для тепловой машины поток x2 связан с x1 соотношением [3]:
После преобразования получим
Подставим результат в (17) и получим smin(x2):
Аппроксимация
С помощью Maple (см. ниже, задача 1) дважды продифференцировав (20) по x2 и подставив x2=0, найдем значение коэффициента d22:
Так как smin(x2) не зависит от x1, значения коэффициентов аппроксимации d11 и d12 равны 0. Уравнения (5) примут вид
они определяют максимальную мощность и соответствующий ей поток теплоты от горячего источника. Программы построения области реализуемости необратимых термодинамических систем в пакете Maple Задача 1. #Расчет коэффициентов аппроксимации restart; #Вид функции sigmamin(x) может быть произвольным и зависит от решаемой задачи. В данном случае мы оставляем sigmamin(x) в общем виде и проводим расчет. Тем самым даем возможность читателю подставить свое значение функции sigmamin в нашу программу и автоматически рассчитать значения коэффициентов аппроксимации для своего случая. #Ввод конкретной функции sigmamin:
#Для нахождения коэффициента d11 необходимо дважды продифференцировать функцию sigmamin по x1, взять значение производной при x1=0 и домножить на ½:
#Для нахождения коэффициента d22 необходимо дважды продифференцировать функцию sigmamin по x2, взять значение производной при x2=0 и домножить на ½:
#Для нахождения коэффициента d12=d21 необходимо взять смешанную производную функции sigmamin по x1 и x2 и домножить ее значение на ½ при x1=0 и x2=0:
Задача 2. #Вид функции F, определяющей границу области реализуемости #Приложение для выражения функции F(x1, x2) в квадратичной форме для тепловой машины #Выпишем уравнения термодинамических балансов в общем виде для тепловой машины (7), (8)
#Для определения границы области реализуемости неравенство в (8) заменим на равенство
#Из уравнения (7) выразим x3:
#Подставим полученное выражение в уравнение (8): #Преобразуем полученное соотношение, собрав все коэффициенты при x1, x2. Это и будет искомое соотношение F(x1, x2)=0 в квадратичной форме
Задача 3. #Построение границы области x1(x2) по условию F(x1, x2)=0 для тепловой машины #Используем выписанную функцию (24) F(x1, x2)=0 #Используем значения коэффициентов ai, ci, dij для тепловой машины: a1:=1; a2:=1; a3:=1;
d11:=0; d12:=0; d21:=0; #Решаем получившееся уравнение относительно x1 и получаем функцию для расчета границы области x1(x2):
Задача 4. #Нахождение точки экстремума restart; #Используем выписанную функцию (24): F(x1,x2)=0 #Выпишем первое уравнение системы (5)
#Выразим x2 из выписанного уравнения:
#Подставим полученное соотношение в функцию F(x1, x2)=0 (24) и сгруппируем члены при x1:
#Найдем дискриминант полученного квадратного уравнения
#Если найденный дискриминант d больше или равен нулю, поток x1 ограничен сверху и точка экстремума В статье проанализированы общие свойства множества реализуемых режимов необратимых термодинамических систем. Показано, что задача построения этого множества может быть решена с использованием программных средств пакета Maple. В качестве примера построена область реализуемости тепловой машины. Литература 1. Хейвуд Р. Термодинамика равновесных процессов. М.: Мир, 1983. 2. Орлов В.Н., Розоноэр Л.И. Оценки эффективности управляемых термодинамических процессов на основе уравнений баланса энергии, вещества и энтропии: матер. X Всесоюз. совещ. по проблемам управления. М.: Наука, 1986. 3. Цирлин А.М. Математические модели и оптимальные процессы в макросистемах. М.: Наука, 2006. 4. Розоноэр Л.И., Цирлин А.М. Оптимальное управление термодинамическими системами // Автоматика и телемеханика. 1983. № 1. С. 70–79; № 2. С. 88–101; № 3. С. 50–64. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2253 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. | Версия для печати с комментариями |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Проблемы управления конфигурациями в процессе разработки программного обеспечения встроенных систем
- Программный комплекс для разметки и унифицированного описания лица индивида по фотоизображению
- Разработка математических моделей и создание программного обеспечения для управления процессами непрерывного литья заготовок из цветных металлов
- Комплекс программ для определения параметров электрических дуг трехфазного переменного тока, горящих на горизонтальную поверхность
- Программный комплекс поддержки учебного процесса
Назад, к списку статей
Comments
автор: Виктория [2009-08-19 14:08:40]Оценка пользователя: 10 баллов



 ,
, 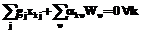 ,
, , (1)
, (1) – интенсивность j-го материального потока;
– интенсивность j-го материального потока; 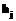 – его удельная энтальпия;
– его удельная энтальпия;  – концентрация в нем k-го вещества;
– концентрация в нем k-го вещества;  – интенсивность i-го потока тепла;
– интенсивность i-го потока тепла;  – температура этого потока на контрольной границе системы; p – потребляемая механическая работа (мощность);
– температура этого потока на контрольной границе системы; p – потребляемая механическая работа (мощность);  – скорость n-й химической реакции;
– скорость n-й химической реакции; 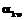 – стихиометрический коэффициент, с которым k-я компонента входит в уравнение n-й реакции (
– стихиометрический коэффициент, с которым k-я компонента входит в уравнение n-й реакции (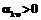 для образующихся и
для образующихся и 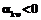 для расходующихся веществ); s – производство энтропии (диссипация) в системе, которая зависит от потоков энергии и вещества. Коэффициенты в уравнениях (1) зависят от внешних факторов и от параметров самой системы – коэффициентов тепло- и массопереноса, интенсивных переменных (температуры, давления, концентрации и др.).
для расходующихся веществ); s – производство энтропии (диссипация) в системе, которая зависит от потоков энергии и вещества. Коэффициенты в уравнениях (1) зависят от внешних факторов и от параметров самой системы – коэффициентов тепло- и массопереноса, интенсивных переменных (температуры, давления, концентрации и др.).
 ,
,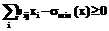 . (2)
. (2) (3)
(3)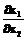 в начале координат представляет собой коэффициент эффективности в обратимом процессе. Она положительна и равна
в начале координат представляет собой коэффициент эффективности в обратимом процессе. Она положительна и равна . (4)
. (4)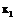 :
: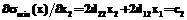 ,
,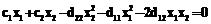 . (5)
. (5)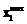 , которому соответствует значение
, которому соответствует значение 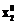 .
. и покажем на примере тепловой машины последовательность построения этих областей.
и покажем на примере тепловой машины последовательность построения этих областей. , холодного – с температурой
, холодного – с температурой  и рабочего тела, поочередно контактирующего с каждым из резервуаров и производящего механическую работу с интенсивностью p. Машина отбирает поток тепла
и рабочего тела, поочередно контактирующего с каждым из резервуаров и производящего механическую работу с интенсивностью p. Машина отбирает поток тепла  от горячего источника, отдает поток
от горячего источника, отдает поток  холодному источнику и вырабатывает мощность p. Если процесс циклический, то под упомянутыми потоками будем понимать среднее значение потоков подводимого, отводимого тепла и механической работы (мощности) за цикл. Обмена веществом в данном случае не происходит, n=0.
холодному источнику и вырабатывает мощность p. Если процесс циклический, то под упомянутыми потоками будем понимать среднее значение потоков подводимого, отводимого тепла и механической работы (мощности) за цикл. Обмена веществом в данном случае не происходит, n=0.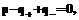
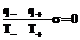 . (6)
. (6)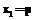 ,
, 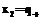 ,
,  и запишем термодинамические балансы для тепловой машины в форме (2), приняв во внимание, что smin или ее аппроксимация квадратично зависят от параметров системы:
и запишем термодинамические балансы для тепловой машины в форме (2), приняв во внимание, что smin или ее аппроксимация квадратично зависят от параметров системы: , (7)
, (7)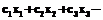
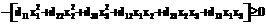 .(8)
.(8)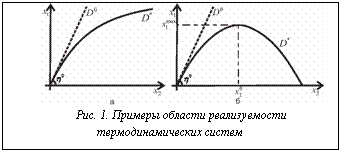
 (9)
(9) . (10)
. (10) . (11)
. (11) ,
,  .
.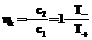 (12)
(12) и
и  соответственно и закон теплопередачи в форме
соответственно и закон теплопередачи в форме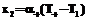 ,
, 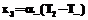 . (13)
. (13) , (14)
, (14) .
.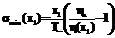 . (15)
. (15) ,
,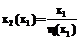 (16)
(16)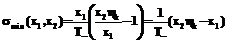 . (17)
. (17)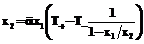 . (18)
. (18)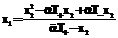 . (19)
. (19) . (20)
. (20)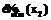 имеет вид:
имеет вид: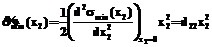 . (21)
. (21) . (22)
. (22) ,
, 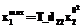 ; (23)
; (23)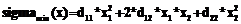


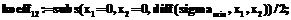
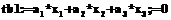
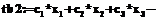
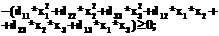
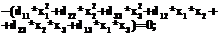



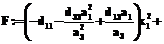
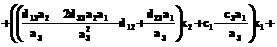
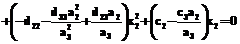 . (24)
. (24)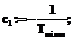


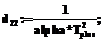 d13:=0; d23:=0; d33:=0;
d13:=0; d23:=0; d33:=0;
 .
.