Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Визуализация и анализ баз знаний интеллектуальных систем
Аннотация:
Abstract:
| Автор: Щуревич Е.В. () - | |
| Ключевые слова: муравьиные алгоритмы, кластеризация, визуализация знаний, база знаний |
|
| Keywords: ant colony optimization, clusterization, , knowledge base |
|
| Количество просмотров: 13115 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
Для интеллектуальных систем, основанных на знаниях, большую роль играет наблюдение за базой знаний, ее формированием и изменением во времени. Однако из-за больших объемов и сложности информации, которой оперируют такие системы, эта задача требует большого количества ресурсов и становится трудновыполнимой. В данной работе представлена модель кластеризации и визуализации знаний для оценки текущего состояния базы знаний. Модель визуализации знаний основана на отображении многомерного пространства базы знаний на двухмерное и включает в себя построение интуитивно понятного графического изображения знаний системы с учетом их пространственной структуры. В связи с тем, что отображению подлежат большие объемы информации, очень сложно сделать выводы о структуре сформированной базы. Дополнительная сложность в том, что визуализация является отображением многомерного пространства знаний на двухмерное, а это неизбежно влечет за собой наложение изображений различных, не связанных между собой частей базы знаний друг на друга, еще больше затрудняя восприятие. Таким образом, основными задачами при визуализации базы знаний являются выбор методики ограничения отображаемой части базы и разработка алгоритма отображения структуры знаний на двухмерное пространство с максимальным сохранением их пропорций и интуитивно понятным изображением основных количественных характеристик базы знаний. Рассмотрим интеллектуальную систему, которая создавалась в предположении, что все множество фраз естественного языка представимо в виде суперпозиций понятий. Элементарными структурными единицами знаний в этой системе являются понятия, объединяющие в себе слова, схожие по смыслу. Перевод фраз естественного языка в суперпозиции понятий позволяет выделить связи между понятиями. Так, например, фраза «в вазе стоит букет» представима в виде суперпозиции стоять (букет, ваза), которая дает две связи: стоять – букет (функциональная связь) и стоять – ваза (пространственная связь). Близость понятий, между которыми существует связь, определяется ее повторностью – количеством встречающихся в тексте суперпозиций, реализующих данную связь. Исходя из этого, определим понятие длины связи – величины, обратно пропорциональной повторности: Таким образом, длина любой связи будет находиться в промежутке [1/Rmax, 1]. Для отображения многомерной структуры знаний на двухмерное пространство в данной работе используется антиградиентный метод. Однако знания не существуют обособленно, они объединены в некие блоки, представляющие собой те или иные знания о мире. Назовем такие блоки кластерами. Кластеризация текстов позволяет не только отделить друг от друга знания из разных областей, но и отсечь знания, не вошедшие ни в один кластер, а значит, имеющие малый вес в данной базе знаний. Эти знания (понятия и связи, их образующие) можно не учитывать при визуализации знаний, уменьшая количество информации для анализа специалистом и, соответственно, облегчая его работу. Алгоритмы кластеризации Для разложения текста естественного языка на суперпозиции с целью извлечения понятий и связей между ними авторы использовали разработки проекта AOT.ru [1]. Понятия и связи из суперпозиций составляют базу знаний системы. Далее к полученной базе знаний применялся муравьиный алгоритм – метод оптимизации, базирующийся на моделировании поведения колонии муравьев. Основу социального поведения муравьев составляет самоорганизация – множество динамических механизмов, обеспечивающих достижение системой глобальной цели в результате низкоуровневого взаимодействия ее элементов. Принципиальной особенностью такого взаимодействия является использование элементами системы только локальной информации. При этом исключаются любое централизованное управление и обращение к глобальному образу, репрезентирующему систему во внешнем мире. Самоорганизация является результатом взаимодействия следующих четырех компонентов: случайность, многократность, положительная обратная связь, отрицательная обратная связь. Для применения муравьиных алгоритмов к представленной задаче необходимо соответствующим образом уточнить реализацию четырех составляющих самоорганизации муравьев. Было предложено конкретизировать алгоритм следующим образом. Многократность взаимодействия реализуется итерационным движением по графу взаимосвязей базы знаний одновременно несколькими муравьями. Каждый муравей начинает маршрут из своей точки – понятия базы знаний. Положительная обратная связь реализуется как имитация поведения муравьев типа «оставление следов – перемещение по следам». Для данной задачи это поведение подчиняется следующему стохастическому правилу: вероятность выбора ребра в качестве следующего на пути пропорциональна количеству феромона на нем. Применение такого вероятностного правила обеспечивает реализацию и другой составляющей самоорганизации – случайности. Количество откладываемого муравьем феромона на ребре графа связности обратно пропорционально длине маршрута. Использование только положительной обратной связи приводит к тому, что все муравьи двигаются одним и тем же маршрутом. Во избежание этого используется отрицательная обратная связь – испарение феромона. Время испарения не должно быть слишком большим, так как при этом возникает опасность сходимости популяции маршрутов к одному. С другой стороны, время испарения не должно быть и слишком малым, так как это приводит к быстрому забыванию, потере памяти колонии и, следовательно, к некооперативному поведению муравьев. Пусть для каждого муравья переход из понятия i в понятие j зависит от двух составляющих – видимости и виртуального следа феромона. Видимость – это величина, обратная расстоянию (hij=1/Dij, где Dij – длина связи (расстояние) между понятиями i и j) , а также локальная ста- тистическая информация, выражающая эвристическое желание посетить понятие j из понятия i: чем ближе понятие, тем больше желание посетить его. Виртуальный след феромона на ребре (i, j) представляет подтвержденное муравьиным опытом желание посетить понятие j из понятия i. В отличие от видимости след феромона является более глобальной и динамической информацией – она изменяется после каждой итерации алгоритма, отражая приобретенный муравьями опыт. Количество виртуального феромона на ребре (i, j) на итерации t обозначим через tij(t). Важную роль в муравьиных алгоритмах играет вероятностно-пропорциональное правило, определяющее вероятность перехода k-го муравья из понятия j в понятие i на t-й итерации. В данном случае было предложено использовать следующую формулу для этого правила:
После прохождения ребра каждый муравей k откладывает на ребре (i, j) количество феромона Dtij,k(t), обратно пропорциональное параметру Q. Для исследования всего пространства решений необходимо обеспечить испарение феромона. Обозначим коэффициент испарения феромона через pÎ[0, 1]. Тогда правило обновления каждого вида феромона примет вид: В начале работы алгоритма количество феромона каждого вида принимается равным небольшому положительному числу t0. Общее количество муравьев в колонии остается постоянным. В результате работы муравьиного алгоритма получен граф связности базы знаний с некоторым количеством феромона на его ребрах. Используем эти данные для кластеризации знаний. Рассмотрим варианты кластеризации на основании длины связей и количества феромона на связях. Для обоих вариантов кластеризация начинается с выбора ребра с максимальным (или близким к максимальному) количеством феромона на нем (оно будет являться начальной точкой распространения очередного кластера). Ограничим начальное ребро для кластера количеством феромона K×tmax, где K – некоторый коэффициент. Начальное ребро не должно принадлежать ни одному из уже определенных кластеров. Понятия, которые связывает выбранное ребро, становятся элементами кластера. Дальнейшее распространение кластера происходит по ребрам, исходящим из первых двух понятий, причем включение очередной связи (и понятия на другом ее конце) в кластер зависит от варианта кластеризации. Для кластеризации по длине связей ограничением является их суммарная длина от одного из двух начальных понятий до любого из понятий, включаемых в этот же кластер. Для кластеризации по количеству феромона ограничена сумма величин, обратно пропорциональных количеству феромона на ребрах входящих в граф связей (чем больше количество феромона на связи, тем меньше включение ее в состав кластера приближает нас к границе). Сравнение моделей кластеризации Сравним результаты описанных вариантов кластеризации на одинаковых коротких текстах. На рисунках 1–3, иллюстрирующих примеры, длина каждой связи обозначена числом, а количество феромона – толщиной линии (чем больше феромона, тем толще линия, изображающая связь). Понятия, объединенные в результате кластеризации в один блок, изображаются однаковыми по форме. Будем проводить кластеризацию для каждого варианта по нескольку раз, чтобы отследить изменчивость результатов под влиянием случайной составляющей муравьиных алгоритмов. Рассмотрим пример энциклопедического текста, характеризующегося высокой сложностью используемых языковых структур. Пример 1. Техника – это общее название различных приспособлений, механизмов и устройств, не существующих в природе, а изготовленных человеком. Слово «техника» также означает «способ изготовления чего-либо» – например, техника живописи, техника выращивания картофеля и т.п. Основное назначение техники – избавление человека от выполнения физически тяжелой или рутинной работы, чтобы предоставить ему больше времени для творческих занятий, облегчить повседневную жизнь. Различные технические устройства позволяют значительно повысить эффективность и производительность труда, более рационально использовать природные ресурсы, а также снизить вероятность ошибки человека при выполнении каких-либо сложных операций. Универсальная классификация технических средств еще не создана. Техника классифицируется по областям применения (промышленная, бытовая, вычислительная техника, транспорт и т.д.). Дополнительно технику можно разделить на производственную (станки, инструменты, средства измерения и т.д.) и непроизводственную (бытовая техника, легковой транспорт, техника для досуга). Отдельным классом также стоит военная техника, в которую входят все технические устройства и машины, предназначенные для поддержания обороноспособности и ведения боевых действий на суше, в море, воздухе и космосе.
По результатам эксперимента можно сделать вывод, что кластеризация по феромону формирует более компактные кластеры, что происходит не только благодаря, возможно, более жесткому ограничению, но и в результате выбора муравьями определенных маршрутов перемещения по графу связностей базы знаний. Рассмотрим текст, взятый из детской энциклопедии. Такие тексты характеризуются меньшей сложностью языковых конструкций, а также более частым использованием синонимов для обозначения одних и тех же предметов. Результатом такой структуры текста является малая повторность связей между понятиями, в связи с чем основная нагрузка на выявление кластеров ложится на муравьиные алгоритмы и, соответственно, увеличивается влияние стохастического фактора. Для стабилизации результатов алгоритма возьмем текст не слишком маленького объема. Пример 2. Леса – самые важные экосистемы Земли. Лес – это природное сообщество, в котором живет много видов растений и животных. Различают леса таких видов: тайга, хвойные, смешанные, широколиственные, редколесье, субтропические, высокогорные и влажные тропические леса. В лесах обитает большая часть всех растений и животных суши. Леса не только обогащают воздух кислородом, они еще поглощают огромное количество газов и пыли. Кроме того, они дают кров многим животным. Лесами покрыто около 1/3 земной поверхности.
Использование текста среднего размера позволяет увеличить повторность связей, в результате чего оба алгоритма кластеризации в большинстве случаев выдают полностью идентичные кластеры. Итоговый объем кластера в данном случае значительно меньше, чем в предыдущем примере. На основании изложенного можно сделать следующие выводы. Кластеризация позволяет выделить относительно небольшие по объему части базы знаний, по которым специалист может судить о текущем состоянии базы знаний интеллектуальной системы, а также о качестве и динамике ее развития. Степень детализации изображения знаний для анализа можно регулировать с помощью коэффициентов алгоритмов кластеризации, ограничивающих распространение кластеров от начальной связи. Выбранные формы представления знаний в графическом виде являются интуитивно понят- ными и значительно увеличивают скорость ана- лиза базы человеком. Полученная картинка является своего рода кратким содержанием всех знаний, имеющихся в базе. По этому изображению легко понять, о чем идет речь в анализируемом тексте. Литература 3. Автоматическая обработка текста. URL: http://www. aot.ru (дата обращения: 02.04.2009). 4. Сотник С.Л. Основы проектирования систем искусственного интеллекта: курс лекций / 1997–1998. 5. Штовба С.Д. Муравьиные алгоритмы // Exponenta Pro. 2003. № 4. С. 70–75. 6. Щуревич Е.В., Крючкова Е.Н. Моделирование и анализ знаний в системах искусственного интеллекта // Вестник Алтайского гос. технич. ун-та им. И.И. Ползунова. Барнаул, 2006. № 2. С. 173–177. | ||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2262 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Кластеризация документов интеллектуального проектного репозитария на основе FCM-метода
- Логический анализ корректирующих операций для построения качественного алгоритма распознавания
- Программная система диагностики заболевания по хроматограмме образца сыворотки крови
- Общий подход к проведению компьютерных экспериментов по индуктивному формированию знаний
- Построение динамической мультиагентной модели с использованием классификации трендов
Назад, к списку статей



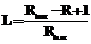 , где L – длина связи; R – повторность связи; Rmax – максимальная повторность в базе знаний.
, где L – длина связи; R – повторность связи; Rmax – максимальная повторность в базе знаний.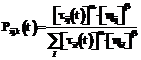 , где α и b – регулируемые параметры, задающие вес феромона и все видимости при выборе маршрута.
, где α и b – регулируемые параметры, задающие вес феромона и все видимости при выборе маршрута.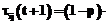
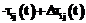 ,
, 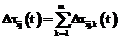 , где m – количество муравьев в колонии.
, где m – количество муравьев в колонии. вариант 1
вариант 1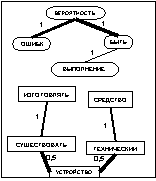 вариант 2
вариант 2
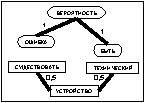
 а)
а) б)
б)