Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная реализация бинарных арифметических операций для нечетких чисел
Аннотация:
Abstract:
| Авторы: Круглов В.В. (byg@yandex.ru) - Филиал Московского энергетического института (технического университета) в г. Смоленске, доктор технических наук, Балашов О.В. (andrey@uskov.net) - Российский университет кооперации, г. Смоленск, кандидат технических наук | |
| Ключевые слова: программная реализация арифметических операций над нечеткими числами, бинарные арифметические операции, нечеткие числа, нечеткие множества |
|
| Keywords: , , , fuzzy sets |
|
| Количество просмотров: 12148 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
Как известно, аппарат нечетких множеств и нечеткой логики с успехом применяется для решения задач, в которых исходные данные ненадежные и слабоформализованные. Одним из основных понятий данного аппарата является понятие нечеткого числа. Нечеткие числа – это нечеткие переменные, определенные на числовой оси, то есть нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности mA(x)Î[0,1], где x – действительное число, то есть xÎR. Расширенные бинарные арифметические операции (сложение, умножение и пр.) для нечетких чисел определяются через соответствующие операции для четких чисел с использованием принципа нечеткого обобщения Заде следующим образом [1, 2]. Пусть А и В – нечеткие числа и С=А где mA(x), mB(y) – функции принадлежности нечетких чисел-операндов, mC(z) – функция принадлежности нечеткого числа – результата арифметической операции. Отсюда: С= С= С= С= Для вычисления результата арифметической операции разработано несколько алгоритмов. Так, в [3] предложен алгоритм перебора, позволяющий найти приблизительное (с любой точностью) значение функции принадлежности для любой точки носителя результата в соответствии с приведенными определениями. В статье [4] рассматриваются нечеткие числа с кусочно-непрерывной функцией принадлежности; доказана теорема, позволяющая достаточно легко отыскивать точное значение степени принадлежности для любого элемента носителя результата арифметической операции. Соответствующий алгоритм применим для определения расширенных бинарных арифметических операций, но требует численного решения нелинейных уравнений. В других известных реализациях этих операций, приведенных, например, в [2], предполагается задание нечетких чисел на дискретных носителях, что является определенным неудобством при их выполнении, связанным с необходимостью большого объема ручных вычислений. Укажем, что все отмеченные алгоритмы рассчитаны на ручные вычисления. Между тем программная реализация таких операций легко достигается при использовании систем компьютерной математики, таких как MathCAD, MATLAB, Maple и др. [5]. Рассмотрим для примера операцию умножения, записав ее в соответствии с приведенными формулами следующим образом:
Здесь аргумент y в функции принадлежности второго операнда заменен на аргумент z/x (что следует из задаваемой операции z=x×y).
Нечеткие числа A и B заданы трапецеидальными функциями принадлежности:
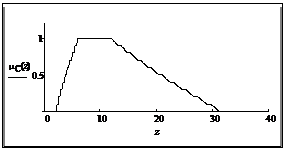
Необходимо найти нечеткое число C= Решение задачи в среде MathCAD (листинг MathCAD): mA(x):= mB(y):= mC(z):= Формулы (1) и (2) задают трапецеидальные функции принадлежности операндов, программный цикл – вычисление дискретных значений функции принадлежности результата, график которой представлен на рисунке. Из специфических вычислительных особенностей MathCAD здесь использованы только функции min и max и способность создавать цикл вычислений – возможности, которыми обладают все современные системы компьютерной математики. Аналогично программно реализуются другие бинарные арифметические операции над нечеткими числами. Так, исходная формула для суммирования двух нечетких чисел будет иметь вид:
поскольку в соответствии с этой операцией z=x+y и y=z–x, алгоритм решения задачи в среде MathCAD практически повторяет приведенный и т.д. Предложенная схема программной реализации бинарных арифметических операций для нечетких чисел легко реализуема в известных системах компьютерной математики – MathCAD, MATLAB и др. В статье приведен пример подобной реализации для операции умножения в среде MathCAD. Полученные результаты могут использоваться, в частности, в системах поддержки принятия решений. Литература 1. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях. Тюмень: Изд-во Тюменского гос. ун-та, 2000. 2. Штовба С.Д. Проектирование нечетких систем средствами MATLAB. М.: Горячая линия – Телеком, 2007. 3. Модели принятия решений на основе лингвистической переменной / А.Н. Борисов [и др.]. Рига: Зинатне, 1992. 4. Dubois D., Prade H. Fuzzy Real Algebra: Some Results // Fuzzy Sets a. Systems. 1979. Vol. 2. № 4, pp. 327–348. 5. Дьяконов В.П. Mathcad 11/12/13 в математике: справочник. М.: Горячая линия – Телеком, 2007. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2264 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Кластеризация документов интеллектуального проектного репозитария на основе FCM-метода
- Архитектура подсистемы нечеткого вывода для оптимизатора баз знаний
- Нечеткая когнитивная карта как инструмент моделирования инновационной деятельности на региональном уровне
- Некоторые вопросы количественной оценки производительности детекторов границ
- Интеллектуальные процедуры планирования и управления в производственных системах геофизического приборостроения
Назад, к списку статей



 – нечеткая операция, соответствующая операции * над обычными числами. Тогда (используя здесь и в дальнейшем обозначения
– нечеткая операция, соответствующая операции * над обычными числами. Тогда (используя здесь и в дальнейшем обозначения  вместо
вместо  и
и 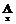 вместо
вместо  ) можно записать:
) можно записать: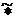 B ÛmC(z)=
B ÛmC(z)=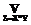 (mA(x)LmB(y)),
(mA(x)LmB(y)), ÛmC(z)=
ÛmC(z)=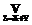 (mA(x)LmB(y)),
(mA(x)LmB(y)),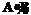 Û mC(z)=
Û mC(z)=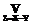 (mA(x)LmB(y)),
(mA(x)LmB(y)), Û mC(z)=
Û mC(z)=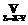 (mA(x)LmB(y)),
(mA(x)LmB(y)), Û mC(z)=
Û mC(z)=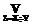 (mA(x)LmB(y)).
(mA(x)LmB(y)). .
. Приведенное соотношение весьма просто реализуется, в частности, средствами MathCAD, что удобнее всего показать на следующем примере.
Приведенное соотношение весьма просто реализуется, в частности, средствами MathCAD, что удобнее всего показать на следующем примере.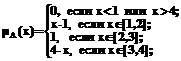 ,
,
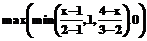 ; (1)
; (1)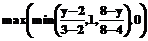 ; (2)
; (2)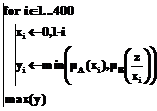 . (3)
. (3)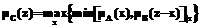 ,
,