Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Компьютерные системы управления поиском решения задач
Аннотация:
Abstract:
| Авторы: Дьячук П.П. () - , Николаева Ю.С. () - | |
| Ключевые слова: ресурсы, пространство поиска, саморегуляция, управление, учебная деятельность |
|
| Keywords: resources, , , control management, |
|
| Количество просмотров: 10861 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
В системах искусственного интеллекта [Рас- сел С., Норвиг П.] проблема поиска решения задач состоит в нахождении алгоритма и соответствующей программы поиска допустимого пути в пространстве состояний из начального в целевое состояние. В настоящей работе предлагается использовать этот подход для организации процесса научения решению задач не искусственного, а естественного разума, осуществляющего реальный поиск решения задачи в пространстве состояний. Для этого используются возможности информационных технологий, которые позволяют отобразить пространство состояний задачи в виде множества ситуаций и задать функцию определения преемника системой кнопок. Нажатие кнопки соответствует тому или иному действию, которое переводит задачу из текущей ситуации в следующую. Последовательность действий и ситуаций в графовом представлении можно рассматривать как путь, который проходит обучающийся в процессе поиска решения задачи. При этом он не обязан быть оптимальным. Однако по мере научения путь, проходимый обучающимся, приближается к оптимальному, то есть со временем его деятельность становится безошибочной. В подходе, использующем пространство состояний, предполагается существование счетного множества s-состояний и множества o-операторов, которые отражают состояния множества s в себя. Решение задачи рассматривается как передвижение в пространстве, определяемом множеством этих состояний, для достижения желаемого множества целевых состояний. Задача решена, когда найдется такая последовательность операторов
что где s0 – некоторое состояние из множества начальных состояний, а sg – из множества целевых состояний. В качестве простого примера опишем граф пространства состояний задачи по преобразованию линейной функции y=kx+b. Данное пространство представляет собой граф, вершины которого находятся в узлах квадратных решеток. Каждой вершине соответствуют два числа (k, b). Первое число, k, соответствует тангенсу угла наклона графика, второе, b, показывает, насколько поднят или опущен график линейной функции вдоль оси Oy. Квадратные решетки соответствуют разным знакам k. Любая вершина графа может быть начальным состоянием графика линейной функции, как и любая вершина может служить целевым состоянием. Например, задача по преобразованию графика линейной функции из начального состояния (1, 0) в целевое (-3, -1). Применим подход поиска решения задач обучающимися в пространстве состояний в компьютерной системе управления учебной деятельностью при научении решению задач. Наложим ограничения на ресурсы: количество учебных действий Y, время их выполнения T. Если воспользоваться приближением равных «стоимостей» действий, то ресурс Y можно рассматривать как сумму денег, которую имеет обучающийся на начало учебной деятельности. Каждое выполняемое действие уменьшает эту сумму на единицу независимо от правильности или неправильности действия. Задача обучающегося состоит в минимизации трат ресурса Y, то есть перехода в процессе научения к оптимальным траекториям деятельности по поиску целевого состояния. Рассмотрим организацию учебной деятельности, в которой полезным результатом является минимум неправильных действий, а ресурс Y выделяется на каждую итерацию (или период работы) отдельно. Итерация под номером i соответствует i-му периоду работы, или i-заданию. Обозначим Yi ресурс, определяющий количество учебных действий в i-м периоде времени для обучающегося. Минимальное число действий, требуемых для решения задач в i-м периоде, обозначим Zi. Если интерпретировать тип обучающегося RiÎ[0; 1] как долю его успешных действий, то, выполняя в i-м периоде объем работ Для того чтобы обучающийся мог изменять свое внутреннее состояние и таким образом перестраивать свою деятельность в процессе научения решению задач, необходимо, чтобы компьютерная система управления обеспечивала дополнительные петли обратной связи, дающей обучающемуся информацию о протекании процесса поиска решения текущей задачи, состоянии имеющихся ресурсов, функции ценности состояния обучающегося. Эта информация подается на вход обучающемуся с помощью таких датчиков, как «расстояние до цели», расхода ресурсов, значений функции ценности состояния обучающегося. Кроме информационных и мотивационных управлений, в системе имеется внедренный агент, который может активно вмешиваться в деятельность обучающегося, выполняя, как и обучающийся, те или иные действия. Воздействия внедренного агента носят институциональный характер. Датчик «расстояние до цели» относится к информационному управлению, которое не препятствует совершению неправильных действий. Частота появления датчика «расстояние до цели» изменяется согласно результатам деятельности обучающегося. Кроме подсистемы, осуществляющей информационное управление в системе, имеется подсистема институциональных управлений. Если обучающийся в процессе работы так расходовал свой ресурс Yi, что его остатка хватает только на то, чтобы дойти до цели и при этом не сделать ни одной ошибки, то, следуя принципу последовательности, система управления включает институциональные управляющие воздействия. Деятельность подсистемы информационных управляющих воздействий сменяется деятельностью подсистемы институциональных управляющих воздействий. Институциональные управляющие воздействия – это целенаправленное ограничение множества возможных действий обучающегося. Вероятно, что первыми управляющими воздействиями, формирующими поведение ребенка, являются институциональные. Они ликвидируют неправильные действия, не позволяя ребенку совершать действия, которые могут нанести ему вред. Решение об этих управляющих воздействиях принимают родители, с этой целью они должны постоянно наблюдать за поведением ребенка и незамедлительно отменять или ликвидировать его неверные действия. По мере взросления ребенка подобного рода управления применяются к нему все реже и реже, уступая место информационному воздействию. Однако в ситуациях, когда действия обучающегося угрожают его здоровью, подобного рода институциональные управления могут применяться. Например, инструктор по вождению автомобиля или самолета, наблюдая за обучающимся, оказывает мягкие информационные воздействия, давая ему возможность совершать действия, не вмешиваясь в них. Как только обучающийся начинает совершать действия, которые могут привести к роковым последствиям, инструктор немедленно отменяет или ликвидирует эти неправильные действия. Каждое действие обучающегося фиксируется системой управления и записывается в специальный протокол. По достижении цели или исчерпании ресурсов система вычисляет долю успешных действий:
где Литература Рассел С., Норвиг П. Искусственный интеллект: современный подход. 2-е изд.; пер. с англ. М.: Издат. дом «Вильямс», 2006. 1408 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2267 |
Версия для печати Выпуск в формате PDF (4.72Мб) |
| Статья опубликована в выпуске журнала № 2 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Система управления бизнес-процессами и административными регламентами
- Проблемы управления конфигурациями в процессе разработки программного обеспечения встроенных систем
- Унифицированное описание функционирования информационных радиоэлектронных систем для оценки программного обеспечения учебно-тренировочных средств
- Моделирование социальных процессов и мультиагентный подход
- Выбор и распределение автотранспортных средств в жизненном цикле автотранспортного предприятия
Назад, к списку статей



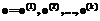 , (1)
, (1)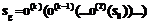 , (2)
, (2)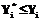 за время Ti, обучающийся достигнет результата
за время Ti, обучающийся достигнет результата 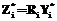 , при этом
, при этом 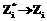 . В модели фигурируют три макропараметра: объем учебных действий
. В модели фигурируют три макропараметра: объем учебных действий 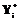 , совершенных в i-й период Ti, соответствующий результат
, совершенных в i-й период Ti, соответствующий результат 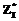 , искомая переменная траектории обучения Ri.
, искомая переменная траектории обучения Ri.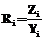 , строится кривая научения. Для запуска процесса научения в первом периоде работ ресурс
, строится кривая научения. Для запуска процесса научения в первом периоде работ ресурс 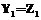 , а ресурс времени
, а ресурс времени 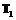 определяется по факту завершения работы. Для второго и последующих периодов работы ресурсы вычисляются рекуррентным образом:
определяется по факту завершения работы. Для второго и последующих периодов работы ресурсы вычисляются рекуррентным образом: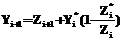 , (3)
, (3)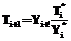 , (4)
, (4)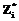 – фактическое количество успешных действий;
– фактическое количество успешных действий; 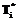 – фактически затраченное время. Предельный переход
– фактически затраченное время. Предельный переход 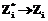 означает, что количество фактически совершенных правильных действий меньше, чем необходимо для решения задач. Полное решение задачи может не состояться из-за нехватки временного ресурса T1. Если временного ресурса достаточно, то, используя институциональное управление, система принудит обучающегося использовать ресурс Yi так, что он обязательно придет в целевое состояние. Поэтому, если фактическое количество правильных действий будет меньше необходимого, связано это будет с нехваткой временного ресурса T1. В то же время из рекуррентной формулы (4) следует, что временной ресурс регулируется темпом выполнения действий обучающимся. Если обучающийся «медленный», то временной ресурс будет больше, если «быстрый», то ресурс будет, соответственно, меньше. То есть временной ресурс будет определяться темпом деятельности обучающегося, что является важной характеристикой его поведения. По мере научения ошибочные действия будут совершаться все реже и реже. Когда Yi будет равным Zi в течение нескольких периодов подряд, можно сделать вывод о том, что обучающийся научился решать поставленные задачи в условиях оптимальных ресурсов. В предлагаемых компьютерных системах управления из-за наличия дополнительных петель обратной связи деятельность обучающихся является саморегулируемой и взаимосвязанной с проблемной средой и личностью обучающегося.
означает, что количество фактически совершенных правильных действий меньше, чем необходимо для решения задач. Полное решение задачи может не состояться из-за нехватки временного ресурса T1. Если временного ресурса достаточно, то, используя институциональное управление, система принудит обучающегося использовать ресурс Yi так, что он обязательно придет в целевое состояние. Поэтому, если фактическое количество правильных действий будет меньше необходимого, связано это будет с нехваткой временного ресурса T1. В то же время из рекуррентной формулы (4) следует, что временной ресурс регулируется темпом выполнения действий обучающимся. Если обучающийся «медленный», то временной ресурс будет больше, если «быстрый», то ресурс будет, соответственно, меньше. То есть временной ресурс будет определяться темпом деятельности обучающегося, что является важной характеристикой его поведения. По мере научения ошибочные действия будут совершаться все реже и реже. Когда Yi будет равным Zi в течение нескольких периодов подряд, можно сделать вывод о том, что обучающийся научился решать поставленные задачи в условиях оптимальных ресурсов. В предлагаемых компьютерных системах управления из-за наличия дополнительных петель обратной связи деятельность обучающихся является саморегулируемой и взаимосвязанной с проблемной средой и личностью обучающегося.