Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм селекции звезд по постоянству угловых расстояний
Аннотация:В статье рассматривается задача селекции звезд для решения проблемы ориентации космических аппаратов по звездам. Приведено обобщенное описание метода отбора звезд, основанного на критерии постоянства взаимных угловых расстояний. Обосновано использование линейной модели для анализа изменения расстояния между двумя светящимися точками.
Abstract:In the following article it is adduced math formulation of stars selection problem in astronavigation. It is given general description of stars selection method, which uses as basis criterion the constancy of mutual digression between the particles. It is substantiated the use of line model for analysis of changing the distance between 2 focuses.
| Авторы: Кружилов И.С. (Krujeelov@mail.ru) - ОАО «Научно-производственное объединение «Геофизика-Космос», г. Москва, Шамаева О.Ю. (shamayevaoy@mpei.ru) - Национальный исследовательский университет «Московский энергетический институт» (доцент), Москва, Россия, кандидат технических наук | |
| Ключевые слова: отбор по скоростям, звездная ориентация, астронавигация |
|
| Keywords: velocity selection, star tracker, astronavigation |
|
| Количество просмотров: 10397 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
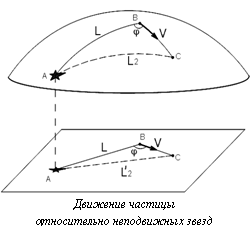
Для ориентации космических аппаратов (KА) в пространстве широко используется ориентация по звездам [1]. Навигационный прибор, вращаясь вместе с КА по орбите, должен по последовательности проекций участков звездного неба на фоне помех выделить звезды и, распознав их на основании бортового каталога, сориентировать спутник в геоцентрической системе координат. Изображение звездного неба проецируется на светочувствительную матрицу дискретной структуры, чаще всего на матрицу пространственно-зарядовой связи (ПЗС). Полученное изображение проходит Алгоритмическую составляющую задачи астронавигации можно разделить на три части: обнаружение светящихся точек на фоне засветки, селекция звезд среди множества светящихся точек (звезд и космических частиц, далее именуемых просто частицами) и поиск звезд в бортовом звездном каталоге. Селекция звезд осуществляется по следующим признакам: по дальности, по уровню сигнала, по оптическому спектру и по скорости движения. Среди упомянутых критериев лишь селекция звезд по угловой скорости [2] имеет характеристики, практически не зависящие от блеска звезды. Однако точность метода зависит от взаимного направления оптической оси прибора и вектора скорости движения КА, а также требует знания абсолютного значения угловой скорости КА. Для повышения точности приборов звездной ориентации необходимо разработать критерий и алгоритм отбора звезд, который был бы лишен указанных недостатков. Пусть xk(t), yk(t) – траектории движения k-й светящейся точки по плоскости анализа (так далее будет называться матрица ПЗС с введенной на ней системой координат). В дискретные моменты tm производятся измерения координат светящихся точек Совокупность всех измерений Обоснование использования линейной модели для анализа скоростей Угловые расстояния между звездами и частицами, а также между самими частицами со временем меняются, тогда как взаимные угловые расстояния между звездами неизменны. На рисунке проиллюстрировано движение светящейся точки из положения B в положение С относительно неподвижной звезды A. Если показать, что изменение углового расстояния L-L2 между звездой и светящейся точкой в зависимости от времени приближенно описывается линейным законом, то для анализа изменения взаимных угловых расстояний достаточно ограничиться лишь одной линейной характеристикой изменения, именуемой далее скоростью изменения взаимного угла. Угловая скорость движения частицы V=(Vx, Vy) относительно неподвижных звезд в рассматриваемой модели считается постоянной. Так как угол обзора прибора составляет порядка 15°, а скорость звезд при орбитальном движении не превышает 10 '/с, для расчетов изменения взаимных угловых расстояний между светящимися точками можно использовать формулы плоской, а не сферической тригонометрии. При данном допущении относительная ошибка вычислений С учетом принятых допущений изменение расстояния S(t) между проекцией звезды и движущейся частицы за время t составит:
здесь x1, y1 – координаты движущейся точки в системе координат, где за центр системы принята звезда. Пусть
Для различных углов φ и значений |V|, равных 5-15 пикс./сек., было проведено имитационное моделирование. Его результаты показали, что при φ=90° значение S(t) является наименьшим среди всех углов φ при фиксированном значении |V| и абсолютное приращение S(t) за время анализа будет настолько мало, что независимо от используемой для описания изменения расстояний модели с трудом различимо на фоне ошибки в определении углового положения источника света. При φ=85° ошибка линейной модели не превышает 3 % от общего приращения функции. Таким образом, линейная модель неэффективна лишь для случая, когда φ=90±5°, что составляет около 5 % от всего диапазона углов. Этот недостаток модели компенсируется разнообразием положения звезд на небесной сфере, в силу чего с высокой вероятностью найдутся такие пары звезд, что угол φ будет отличаться от 90°. Обобщенное описание алгоритма В предлагаемом алгоритме распознавания звезд завязка траекторий движения проекций светящихся точек осуществляется по первым NS кадрам. Точки Как было показано выше, для анализа изменения взаимных угловых расстояний между светящимися объектами достаточно ограничиться лишь их линейной составляющей. Таким образом, выделение группы звезд среди N светящихся точек сводится к анализу вещественной симметричной матрицы М размерности N×N. Каждый элемент матрицы Мi,j – линейная составляющая изменения взаимных угловых расстояний между точками i и j. Если i и j являются звездами, то Мi,j, как уже было отмечено, распределено нормально с нулевым математическим ожиданием Мi,j~N(0, Отбор 4 звезд для распознавания может быть осуществлен на основании критерия максимального правдоподобия путем перебора всех возможных сочетаний по 4 светящиеся точки. Среди всех сочетаний выбирается то, которое с наибольшей вероятностью содержит все звезды. После этого с помощью критерия Неймана–Пирсона с заданными вероятностями ошибок α и β решается, являются ли 4 выбранные точки звездами. Количество всех сочетаний по 4 светящиеся точки равно На этапе предварительного отбора с помощью одного из эмпирических алгоритмов, имеющих сложность O(N2) или O(N2ln(N)), выделяются 5–6 светящихся точек, таких, что среди них с большой вероятностью содержатся 4 звезды. Благодаря этому анализ матрицы размером N×N сводится к анализу матрицы 5×5 (6×6), что уменьшает сложность алгоритма селекции. Процедура окончательного отбора заключается в полном переборе всех сочетаний по 4 из числа предварительно отобранных светящихся точек. Окончательное решение, являются ли точки звездами, принимается на основании критерия Неймана–Пирсона, использование которого усложняется тем, что элементы матрицы М коррелированные. Итак, в работе рассмотрен алгоритм селекции звезд, основанный на критерии постоянства угловых расстояний. Показано, что изменение расстояния между двумя светящимися точками, когда одна из них является звездой, а другая частицей, описывается линейной моделью. На основании этого факта произведена оценка дисперсии погрешности линейной составляющей изменения взаимных угловых расстояний. По сравнению с методом отбора по скоростям предложенный метод имеет следующие преимущества: учитывает не только абсолютное значение, но и направление скорости движения частиц; не требует знания угловой скорости вращения спутника, которая варьируется в достаточно большом диапазоне при маневрах КА; не зависит от взаимного направления оптической оси прибора и вектора вращения КА; устойчив при неравномерном движении КА. К недостаткам метода следует отнести трудоемкость выполнения и алгоритмическую сложность его реализации. Кроме того, предложенная в работе линейная модель изменения взаимных расстояний между звездами и космическими частицами малоэффективна в случае, когда вектор скорости движения частицы почти ортогонален (90±5°) отрезку, соединяющему проекции звезды и частицы. Несмотря на указанные недостатки, алгоритм селекции частиц на основе критерия постоянства угловых расстояний имеет наибольшую надежность и может использоваться в приборах звездной ориентации с достаточными вычислительными ресурсами. Литература 1. Федосеев В.И., Колосов М.П. Оптико-электронные приборы ориентации и навигации космических аппаратов. М.: Логос, 2007. 248 с. 2. Кружилов И.С. Алгоритм распознавания звезд в задаче астронавигации // Информационные средства и технологии: тр. междунар. науч.-технич. конф. М.: Янус-К. 2005. Т. 2. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2325 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Назад, к списку статей



 аналого-цифровое преобразование и поступает для анализа на вычислительный блок прибора.
аналого-цифровое преобразование и поступает для анализа на вычислительный блок прибора.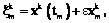
 , где
, где 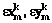 – погрешность измерений, вызванная оптическими искажениями и собственными шумами светочувствительной матрицы. Предполагается, что погрешности распределены нормально:
– погрешность измерений, вызванная оптическими искажениями и собственными шумами светочувствительной матрицы. Предполагается, что погрешности распределены нормально: 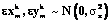 .
.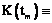
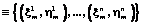 в m-й момент называется m-м кадром. В этой совокупности есть незвездные отметки от незвездных траекторий x(t), y(t), подчиняющихся неизвестному случайному закону движения. По последовательности кадров K(t1), ..., K(tm) требуется построить алгоритм, обнаруживающий траектории звезд, сопровождающий траектории, а также после n кадров выдающий решение о 4 звездах и взаимные угловые расстояния, по которым далее определяется ориентация.
в m-й момент называется m-м кадром. В этой совокупности есть незвездные отметки от незвездных траекторий x(t), y(t), подчиняющихся неизвестному случайному закону движения. По последовательности кадров K(t1), ..., K(tm) требуется построить алгоритм, обнаруживающий траектории звезд, сопровождающий траектории, а также после n кадров выдающий решение о 4 звездах и взаимные угловые расстояния, по которым далее определяется ориентация.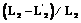 составит не более 1 % .
составит не более 1 % .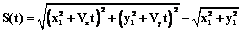 , (1)
, (1)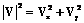 – квадрат модуля скорости;
– квадрат модуля скорости;  – расстояние между точками; φ – угол между направлением вектора скорости и отрезком, соединяющим проекции светящихся точек в начальный момент. В принятых обозначениях выражение (1) примет вид
– расстояние между точками; φ – угол между направлением вектора скорости и отрезком, соединяющим проекции светящихся точек в начальный момент. В принятых обозначениях выражение (1) примет вид . (2)
. (2)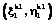 ,
, 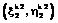 , ... ,
, ... , отождествляются с одной траекторией, если они с заданной вероятностью лежат на одной прямой. Дальнейшее сопровождение траекторий осуществляется методом экспоненциального сглаживания. За время сопровождения накапливается статистика о взаимных угловых расстояниях и параметрах их изменения, используемая для работы алгоритма и распознавания в бортовом каталоге.
отождествляются с одной траекторией, если они с заданной вероятностью лежат на одной прямой. Дальнейшее сопровождение траекторий осуществляется методом экспоненциального сглаживания. За время сопровождения накапливается статистика о взаимных угловых расстояниях и параметрах их изменения, используемая для работы алгоритма и распознавания в бортовом каталоге.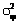 ). Если в паре есть хотя бы одна не звезда, то Мi,j подчиняется в соответствии с выражением (2) случайному закону с математическим ожиданием, отличным от нуля.
). Если в паре есть хотя бы одна не звезда, то Мi,j подчиняется в соответствии с выражением (2) случайному закону с математическим ожиданием, отличным от нуля.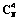 , поэтому асимптотическая сложность алгоритма распознавания составит O(N4). С учетом большого объема обрабатываемых данных и ограничений, накладываемых на время обработки и вычислительную мощность прибора, такая сложность алгоритма неприемлема. Для уменьшения времени распознавания алгоритм можно разделить на два этапа – предварительный и окончательный отбор.
, поэтому асимптотическая сложность алгоритма распознавания составит O(N4). С учетом большого объема обрабатываемых данных и ограничений, накладываемых на время обработки и вычислительную мощность прибора, такая сложность алгоритма неприемлема. Для уменьшения времени распознавания алгоритм можно разделить на два этапа – предварительный и окончательный отбор.