Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Параллельный адаптивный предобусловливатель CPR в задаче фильтрации
Аннотация:Рассмотрена адаптивная модификация предобусловливателя CPR применительно к системам, возникающим при аппроксимации систем дифференциальных уравнений в частных производных для задач фильтрации многокомпонентной смеси в пористой среде. На тестовых и реальных моделях газонефтяных месторождений Западной Сибири проведены вычислительные эксперименты в составе российского промышленного комплекса гидродинамического моделирования на параллельных ЭВМ, подтверждающие эффективность алгоритма.
Abstract:The adaptive modification of Constrained Pressure Residual method of preconditioning are considered concerning to the systems that appears from discretization of systems of partial differential equations which describes multicomponent fluid flow in porous media. The numerical experiments using real parallel hydrodynamic simulator on the real oil fields in Western Siberia demonstrated efficiency of the method.
| Автор: Горелов И.Г. (chronosphere@mail.ru) - Московский государственный университет им. М.В. Ломоносова | |
| Ключевые слова: течение вязкой жидкости в пористой среде, параллельный предобусловливатель, cpr-метод |
|
| Keywords: fluid flow in porous media, parallel preconditioner, CPR method |
|
| Количество просмотров: 6528 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
Неотъемлемой частью современных методов добычи углеводородов являются построение и анализ математической модели месторождения, позволяющей сделать прогноз на несколько лет вперед и принять наиболее оптимальную схему разработки. При этом неизбежно возникает необходимость решения задачи фильтрации вязкой сжимаемой жидкости в пористой среде. Большие размеры моделируемых газонефтяных пластов, а также высокий уровень детализации требуют использования для расчетов дорогостоящего оборудования. Расчет многих моделей может длиться несколько часов, а иногда и дней. Это приводит к тому, что построение более быстрых методов расчета является важной задачей моделирования. Одним из наиболее распространенных методов описания течения многокомпонентной смеси в пористой среде является следующая система уравнений в трехмерной области [1]:
Искомые величины: – молярные плотности компонент; Величины
где
Существует множество методов решения данной системы линейных алгебраических уравнений, в том числе несколько алгоритмов ее предобусловливания. Одним из них является так называемый метод Constrained Pressure Residual, или CPR, который основан на особой структуре получающейся матрицы Классический метод CPR базируется на построении по матрице
по
где Суть адаптивного алгоритма CPR (ACPR или PACPR в параллельном случае) заключается в использовании для построения подматрицы элементов, необязательно соответствующих переменной давления, а выбираемых исходя из некоторого другого условия. Например, можно использовать критерий принадлежности фронту. Под фронтом при этом понимаются блоки, значения неизвестных в которых меняются наиболее сильно на данном временном шаге. Все дальнейшие преобразования изменяются соответствующим образом. Принадлежность фронту определяет, какие из элементов должны использоваться при построении подматрицы, а за их количество отвечает набор параметров Параллельные версии методов CPR и ACPR были реализованы в виде программных модулей и протестированы в составе российского промышленного программного комплекса гидродинамического моделирования. Множество блоков фронта определялось посредством анализа грубого решения, получающегося в результате проведения одной итерации базового алгоритма решения линейной системы с матрицей Многопроцессорные версии алгоритмов базируются на методе перекрытия расчетных областей в разных процессах [4]. Численные эксперименты проводились на трех различных моделях реальных месторождений в Западной Сибири. Тестовый стенд – это машина с 8 ядрами с общей памятью объемом 16 Гб. За время работы принималось время расчета всей модели, включая чтение входных данных, построение якобиана и т.д. Целью тестирования было определение оптимального набора варьируемых параметров, а также практическая проверка работоспособности и эффективности алгоритма с точки зрения промышленного применения. Результаты вычислений приведены в таблице (параллельные версии ILU и CPR – предельные случаи параллельного ACPR).
Из нее видно, что наибольшая скорость работы достигается при различных значениях параметров метода при переходе от модели к модели. Кроме того, эксперимент показал, что использовать для построения подматрицы элементы, соответствующие молярным плотностям, нерационально с точки зрения быстродействия. При этом отказ от использования при построении части элементов, соответствующих давлению, напротив, дает положительный эффект. Алгоритм PACPR показывает свою эффективность на реальных промышленных задачах. Однако для его применения необходимо знать набор оптимальных параметров, которые, как показали вычисления, меняются в зависимости от конкретной модели месторождения. Данный метод может быть полезен в том случае, когда требуется многократно пересчитывать одну и ту же модель, постоянно внося небольшие изменения (добавление скважины, изменение свойств среды, проницаемости, начального давления и пр.). В этом случае можно вначале несколькими запусками подобрать оптимальные значения параметров, а затем использовать их при дальнейших многократных расчетах. Кроме того, уменьшение точек синхронизации и, как следствие, хорошая масштабируемость позволяют говорить о росте производительности с ростом числа вычислительных ядер. Литература 1. Aziz K., Settari A., Petroleum Reservoir Simulation. London: Applied Science Publishers, 1979. 2. Wallis J.R., Kendall R.P., Little T.E. Constraint Residual Acceleration of Conjugate Residual Methods, SPE 13536, 1985 Reservoir Simulation Symposium, Texas, February 10–13, 1985. 3. Louis J. Durlofsky, Khalid Aziz, Advanced Techniques for Reservoir Simulation and Modeling of Nonconventional Wells, Date Report August 20, 2004, DOE Award Number:DE-AC26-99BC15213, Stanford University. 4. Капорин И.Е., Коньшин И.Н. Параллельное решение симметричных положительно-определенных систем на основе перекрывающегося разбиения на блоки // Вычислительная математика и математическая физика. 2001. Т. 41. № 4. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2334 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Назад, к списку статей







 (1)
(1)
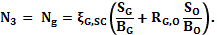
 – давление в нефтяной, водной и газовой фазах;
– давление в нефтяной, водной и газовой фазах; 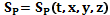 – насыщенности фаз.
– насыщенности фаз. ,
,  ,
,  , k, , , , , , , , ,
, k, , , , , , , , , 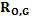 – известные функции, нелинейно зависящие от
– известные функции, нелинейно зависящие от 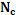 ,
, 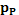 и
и 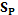 и определенные в [1];
и определенные в [1];  ,
,  и
и  – известные константы;
– известные константы;  – известная функция. Для аппроксимации по времени обычно используется полностью неявная схема, которая при расчете позволяет делать большие относительно других схем шаги по времени. Аппроксимация по пространственным переменным – метод конечных объемов. Задача сводится к системе нелинейных алгебраических уравнений вида:
– известная функция. Для аппроксимации по времени обычно используется полностью неявная схема, которая при расчете позволяет делать большие относительно других схем шаги по времени. Аппроксимация по пространственным переменным – метод конечных объемов. Задача сводится к системе нелинейных алгебраических уравнений вида: , (2)
, (2) ,
, 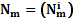 – векторы значений давления и молярных плотностей в блоках сетки. Задача решается методом Ньютона, на каждом его шаге необходимо решать систему с несимметричной матрицей
– векторы значений давления и молярных плотностей в блоках сетки. Задача решается методом Ньютона, на каждом его шаге необходимо решать систему с несимметричной матрицей  , состоящей из блоков размера
, состоящей из блоков размера  :
: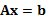 . (3)
. (3) с использованием элементов блоков, соответствующих только переменной давления. Под применением предобусловливателя
с использованием элементов блоков, соответствующих только переменной давления. Под применением предобусловливателя 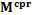 подразумевается следующее:
подразумевается следующее: (4)
(4) строим
строим  (вставляя нули на место неизвестных) и подставляем в
(вставляя нули на место неизвестных) и подставляем в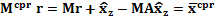 , (5)
, (5) – любой предобусловливатель (например, метод неполного LU-разложения) [2, 3].
– любой предобусловливатель (например, метод неполного LU-разложения) [2, 3].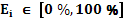 , где
, где  соответствует давлению, а
соответствует давлению, а  и
и 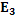 – молярным плотностям. Отметим, что, варьируя количество и тип элементов, участвующих в построении подматрицы, в некоторых предельных случаях получится либо сам алгоритм CPR (
– молярным плотностям. Отметим, что, варьируя количество и тип элементов, участвующих в построении подматрицы, в некоторых предельных случаях получится либо сам алгоритм CPR (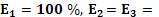 0), либо его версии, соответствующие выбранному базовому предобусловливателю
0), либо его версии, соответствующие выбранному базовому предобусловливателю 
 ). Предобусловливатели CPR и ACPR обладают еще одним параметром – точностью
). Предобусловливатели CPR и ACPR обладают еще одним параметром – точностью  решения локальной системы (4).
решения локальной системы (4). 3
3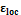
 (%)
(%) (%)
(%) (%)
(%)