Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Построение траектории движения инструмента при многокоординатной обработке
Аннотация:В статье рассматривается задача моделирования движения фрезерного инструмента при многокоординатной обработке. Разработан алгоритм построения траектории движения инструмента. При моделировании обработки заготовки по такой траектории можно рассчитывать на более точное представление обработанной поверхности.
Abstract:In article is considered a problem of milling tool movement at multicoordinate processing modelling. The construction algorithm of a tool movement trajectory is developed. At modelling of preparation processing on such trajectory it is possible to count on more exact representation of the processed surface.
| Авторы: Будник А.И. (budnikalexandr@mail.ru) - Уральский федеральный университет им. Б.Н. Ельцина, г. Екатеринбург, Кац Е.И. (budnikalexandr@mail.ru) - Уральский федеральный университет им. Б.Н. Ельцина, г. Екатеринбург, кандидат технических наук | |
| Ключевые слова: дуга окружности, траектория движения, геометрическое моделирование, многокоординатная обработка |
|
| Keywords: circle arch, movement trajectory, geometrical modelling, multicoordinate processing |
|
| Количество просмотров: 14182 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
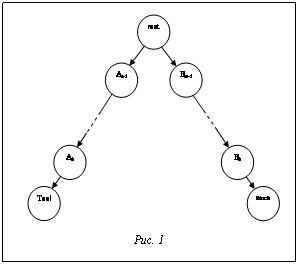
Рассмотрим задачу моделирования движения фрезерного инструмента при многокоординатной обработке. На начальном этапе строится траектория движения инструмента. Исходя из практики применения такого моделирования, траектория должна быть получена в системе координат заготовки. Основная постановка задачи: задана кинематика станка в виде дерева, узлами которого являются оси, осуществляющие вращение или перемещение элементов станка (рис. 1). Каждая ось управляется не более чем одной координатой. Заданы начальные и конечные значения координат для управления станком. Изменение всех координат считается линейным по времени. Необходимо аппроксимировать траекторию движения инструмента NURBS с заданной точностью в системе координат заготовки. Идея аппроксимации траектории заключается в следующем. На первом этапе точным аналитическим методом находим касательные векторы на концах сегмента траектории. Затем строим сегмент рациональной кубической кривой, соответствующий найденным касательным векторам. Далее оцениваем погрешность и разбиваем сегмент траектории на части, если это необходимо. Касательными векторами на концах траектории являются векторы мгновенной скорости движения инструмента. Мгновенная скорость в некоторой точке P(t) равна производной закона движения этой точки по t. Движение инструмента относительно заготовки опишем путем умножения всех точек инструмента на некоторую матрицу, зависящую от t. Тогда
где P(t) – точка на кривой; P0 – точка в начале кадра (P0=P(t)|t=0); M(t) – матрица перемещения инструмента из P0 в P(t). Матрица M(t) представима в виде
где ATool(t), BStock(t) – матрицы движения инструмента и заготовки в системе координат станка соответственно; Ai, Bj – матрицы, характеризующие движение по i-й оси, управляющей положением инструмента, и j-й оси, управляющей положением заготовки. Так как каждая ось управляется определенной переменной, например, определенной станочной координатой, то возможны случаи, когда несколько осей станка управляются одной и той же станочной координатой. Полная производная матрицы M(t) будет выглядеть так:
При моделировании траектории движения инструмента полезно уметь распознавать два частных случая – отрезок и дугу окружности. Такая задача распознавания решается на основе анализа соотношения между вращательным и поступательным движениями. В работе станка также часто встречается движение инструмента по винтовой линии. Важно уметь без решения задачи распознавания моделировать винтовую траекторию движения инструмента кривой, которая в проекции на плоскость вращения представляла бы собой окружность. При моделировании обработки заготовки по такой траектории можно рассчитывать на более точное представление обработанной поверхности. Исходя из этого, был реализован метод, позволяющий находить ось винтовой линии, зная начало и конец кадра, а также векторы скорости в них. Постановка задачи: заданы начало и конец кадра – P0 и P3, векторы мгновенной скорости
Рассмотрим схему (рис. 2). Плоскость γ перпендикулярна вектору оси винтовой линии
В таком случае вектор оси можно представить следующим образом:
где α0, α3 и µ – числовые коэффициенты. Так как в винтовой линии модули мгновен- ных скоростей одинаковы, выражение (5) примет вид
Если необходимо найти лишь направление вектора оси, можно считать коэффициент α=1. Выражение (6) упростится до вида
Из рисунка 2 следует, что
Зная способ нахождения
Здесь угол
где α – угол между векторами Рассматривая рисунок 4, можно написать следующее выражение, из которого выразить α:
где Исходя из рисунка 3, вычисляем радиус проекции винтовой линии:
Модуль линейной скорости постоянен во всех точках винтовой линии, а значит, должен быть равен модулям мгновенных скоростей
где F(β) – качественная функция от β. Учитывая, что
График данной функции изображен ра Так как предельным случаем винтовой траектории движения инструмента является дуга окружности, то β0 ищем следующим образом:
где λ – длина вектора Получив вектор При построении траектории движения инструмента необходимо решить задачу уточнения. Постановка задачи: построить траекторию движения инструмента с погрешностью не более заданной.
Так как отклонение кривых друг от друга заведомо меньше ∆, величина ∆ может служить оценкой (достаточно грубой) отклонения сверху. На рисунке 7 изображена винтовая линия – результат построения траектории. Инструмент одновременно поворачивается вокруг оси винтовой линии и смещается вдоль нее. Движение вдоль оси винтовой линии осуществляется с поворотом. Таким образом, инструмент движется по поверхности тора переменного радиуса. Это сложное движение обусловлено двумя независимыми перемещениями и двумя независимыми вращениями. Данный кадр записан в программе в виде следующих изменений значений координат: B2160.Z-140.Y-500.C30. Соответственно, значения координат XYZABC до и после выполнения кадра выглядят так: (50, 10, 0, 0, 0, 0) и (50, -490, -140, 0, 2160, 30). На основе полученных результатов разработаны алгоритмы и программы моделирования траектории движения инструмента. Соответствующий модуль включен в состав симулятора обработки на станках с ЧПУ. Кроме того, эти результаты являются основой для дальнейших исследований в области геометрического моделирования сложной многокоординатной обработки. Литература 1. Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве; пер с англ. М.: Мир. 1982. 304 с. 2. Препарата Ф., Шеймос М. Вычислительная геометрия. Введение. М.: Мир, 1989. 478 с. 3. Роджерс Д. Алгоритмические основы машинной графики. М.: Мир, 1989. 504 с. 4. Шикин Е.В., Боресков А.В., Зайцев А.А. Начала компьютерной графики. М.: ДИАЛОГ-МИФИ, 1993. 138 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2336 |
Версия для печати Выпуск в формате PDF (4.21Мб) |
| Статья опубликована в выпуске журнала № 3 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Кривая скольжения на инструменте произвольной формы при многокоординатной обработке
- Построение кривой скольжения конического инструмента при многокоординатной обработке
- Структура данных для представления геометрической модели трехмерного объекта
- Показатели безопасности космического аппарата в полете и генерация информации для предупреждения о высокоскоростном взаимодействии
- Метод получения развертки деталей одежды с учетом деформационной способности материала
Назад, к списку статей



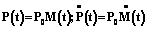 , (1)
, (1) (2)
(2)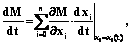 (3)
(3) где M(t) – матрица оси станка; x0, x1, …, xn – переменныe, управляющие станочными осями. Таким образом, после дифференцирования выражение (2) примет вид выражения (3). Количество слагаемых в нем равно количеству координат станка. Если одной координатой управляется несколько осей станка, слагаемое из выражения (3) будет представлять собой сумму нескольких частных производных матрицы станка по этой координате.
где M(t) – матрица оси станка; x0, x1, …, xn – переменныe, управляющие станочными осями. Таким образом, после дифференцирования выражение (2) примет вид выражения (3). Количество слагаемых в нем равно количеству координат станка. Если одной координатой управляется несколько осей станка, слагаемое из выражения (3) будет представлять собой сумму нескольких частных производных матрицы станка по этой координате. и
и 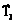 в точках P0 и P3. Необходимо построить винтовую траекторию движения инструмента.
в точках P0 и P3. Необходимо построить винтовую траекторию движения инструмента.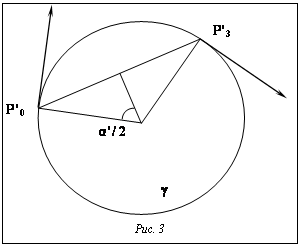 Вначале весь кадр разбивается на дуги не более 180°, для того чтобы можно было представить их рациональными кубическими кривыми. Зная это, можно выявить траекторию в виде отрезка, если векторы мгновенных скоростей на концах траектории коллинеарны. Если нет, то считается, что траектория представляет собой либо дугу окружности, либо винтовую линию. В обоих случаях ось вращения может быть найдена.
Вначале весь кадр разбивается на дуги не более 180°, для того чтобы можно было представить их рациональными кубическими кривыми. Зная это, можно выявить траекторию в виде отрезка, если векторы мгновенных скоростей на концах траектории коллинеарны. Если нет, то считается, что траектория представляет собой либо дугу окружности, либо винтовую линию. В обоих случаях ось вращения может быть найдена.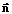 . Из соображений о строении винтовой линии имеем
. Из соображений о строении винтовой линии имеем . (4)
. (4)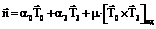 , (5)
, (5)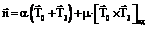 . (6)
. (6) . (7)
. (7) . (8)
. (8)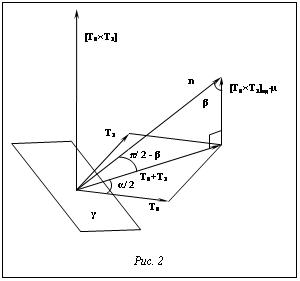 Так как плоскость γ расположена под углом β к плоскости
Так как плоскость γ расположена под углом β к плоскости 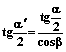
 . (9)
. (9)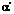 , зависящий от времени, и есть угловая скорость:
, зависящий от времени, и есть угловая скорость: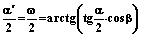 , (10)
, (10) , (11)
, (11)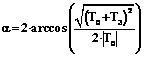 . (12)
. (12)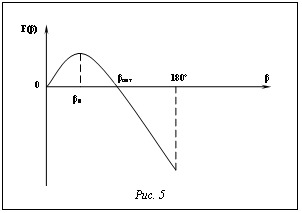 Винтовая траектория движения инструмента также характерна тем, что инструмент имеет постоянный по времени модуль линейной скорости. Отсюда следует, что
Винтовая траектория движения инструмента также характерна тем, что инструмент имеет постоянный по времени модуль линейной скорости. Отсюда следует, что , (13)
, (13)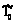 – проекция вектора скорости в начале кадра на плоскость γ.
– проекция вектора скорости в начале кадра на плоскость γ.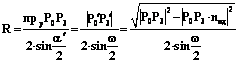 , (14)
, (14)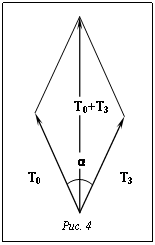 где R – радиус проекции винтовой линии;
где R – радиус проекции винтовой линии;  – длина проекции
– длина проекции 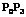 на плоскость γ;
на плоскость γ; 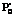 и
и – проекции P0 и P3 на плоскость γ соответственно.
– проекции P0 и P3 на плоскость γ соответственно.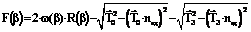 , (15)
, (15)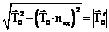 и
и  , получим формулу для F(β):
, получим формулу для F(β):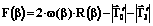 . (16)
. (16)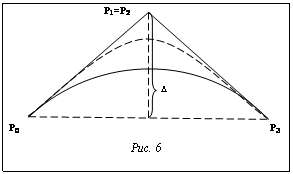 рисунке 5. Из графика видно, что есть некоторое значение βопт, при котором функция F(β) принимает нулевое значение, то есть такую ориентацию вектора
рисунке 5. Из графика видно, что есть некоторое значение βопт, при котором функция F(β) принимает нулевое значение, то есть такую ориентацию вектора  , (17)
, (17) , (18)
, (18) , (19)
, (19) , (20)
, (20)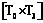 .
. в плоскости γ. Восстановим их до реальных прямых, являющихся продолжениями касательных векторов
в плоскости γ. Восстановим их до реальных прямых, являющихся продолжениями касательных векторов  При рассмотрении данной задачи самым простым решением является деление траектории на несколько сегментов, пока отклонение получившихся в результате частей от истинной кривой не уложится в заданную погрешность (рис. 6).
При рассмотрении данной задачи самым простым решением является деление траектории на несколько сегментов, пока отклонение получившихся в результате частей от истинной кривой не уложится в заданную погрешность (рис. 6).