Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Параллельные алгоритмы и программы для моделирования эйлеровых эластик
Аннотация:Описаны параллельные алгоритмы и программы для моделирования и исследования эластик Эйлера – стационарных конфигураций упругого стержня на плоскости. Продемонстрированы результаты работы программ, показатели эффективности распараллеливания.
Abstract:There are described parallel algorithms and programs for modeling of Euler elasticae – stationary configurations of elastic bar in the plane. Results of work of programs are shown, indices of effective parallelization are demonstrated.
| Авторы: Сачков Ю.Л. (sachkov@sys.botik.ru) - Институт программных систем им. А.К. Айламазяна РАН, г. Переславль-Залесский, Ардентов А.А. (sachkov@sys.botik.ru) - Институт программных систем им. А.К. Айламазяна РАН, г. Переславль-Залесский, доктор физико-математических наук | |
| Ключевые слова: параллельные алгоритмы и программы, оптимальное управление, эластики эйлера |
|
| Keywords: parallel algorithms and programs Image processing, optimal control, euler elasticae |
|
| Количество просмотров: 10695 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
В 1744 г. Леонард Эйлер исследовал задачу о стационарных конфигурациях упругого стержня: дан упругий стержень на плоскости, у которого закреплены положения концов, а также углы наклона стержня на концах. Требуется определить возможные профили стержня при заданных граничных условиях [1]. Эйлер получил дифференциальные уравнения для стационарных конфигураций стержня и описал их возможные качественные типы. Эти конфигурации назвали эйлеровыми эластиками. Задача об эластиках формализуется как следующая задача оптимального управления:
Эластика, минимизирующая значение функционала упругой энергии J, называется оптимальной. С помощью геометрических методов теории управления [2] в работе [3] вычисление оптимальной эластики сведено к решению систем алгебраических уравнений в эллиптических функциях Якоби вида q(y)=q1, где y – начальное значение сопряженной переменной принципа максимума Понтрягина, соответствующее оптимальной эластике с граничным условием q1. В работе [4] описаны разработанные на этой основе последовательные алгоритмы и программы для вычисления оптимальных эластик в системе Mathematica [5]. Цель данной статьи – описание параллельных алгоритмов и программ для вычисления индивидуальной оптимальной эластики по заданным граничным условиям q1, а также серии оптимальных эластик по заданной деформации граничных условий q1(s), sÎ[a,b], и для построения соответствующей анимации. Программы разработаны и протестированы в системе gridMathematica (параллельной версии системы Mathematica) на кластере skif.botik.ru. Описание алгоритмов Вычисление индивидуальной эластики. Специфика задачи в том, что, хотя теоретически доказаны существование и единственность решения системы уравнений q(y)=q1 в определенных областях значений сопряженной переменной, для вычисления этого решения требуется иметь хорошее начальное приближение. Такое приближение отыскивается за счет его многократного случайного выбора на разных вычислительных узлах. Входные параметры: q1 – граничные условия эластики; nnodes – количество узлов суперкомпьютера, которые требуется использовать. Выполняемые операции: На каждом узле запускается решение индивидуальной задачи с разными начальными приближениями. Схема алгоритма решения индивидуальной задачи для одного узла следующая. 1. Произвольно выбираются начальные приближения для решения системы уравнений yb, ye. 2. Запускается поиск решения системы q(y)=q1 методом хорд с использованием значений yb, ye. Результат вычисления записывается в переменную yn. 3. Во временную переменную Решение серии независимых задач. Вычисление серий эластик важно для моделирования квазистатической деформации упругого стержня при непрерывном изменении граничных условий. Особенность задачи заключается в том, что на открытом всюду плотном множестве граничных условий решение системы q(y)=q1 непрерывно зависит от правой части. Однако при переходе через определенные поверхности (поверхности разреза) непрерывная зависимость теряется, и решение системы может испытывать скачок. В первом варианте алгоритма каждая задача серии решается как независимая. (Ниже будет описан другой метод: в областях непрерывной зависимости в качестве начального приближения используется решение, вычисленное на предыдущем шаге.) При переходе через поверхности разреза задачи решаются как индивидуальные. Входные параметры: {qi} – набор граничных условий для эластик; ntests – мощность множества {qi}, количество задач; nnodes – количество узлов, которые требуется использовать. Выполняемые операции: На каждый узел рассылается по одной задаче для вычисления. Вычисление каждой задачи выполняется по схеме, описанной для индивидуальной задачи. Как только какой-нибудь из узлов нашел корень, из множества {qi} выбирается очередная задача и направляется для решения на освободившийся узел. Процесс продолжается до тех пор, пока все задачи не будут решены. Вычисление серии эластик с использованием решения предыдущей задачи. Входные параметры: q1(s) – функция, описывающая непрерывное движение второго конца эластики q1; ntests – количество промежуточных эластик (кадров вычисляемой анимации); nnodes – количество узлов, которые требуется использовать. Выполняемые операции: По функции q1(s) и параметру ntests находится множество задач {qi}, подлежащих решению. Задачи из этого множества делятся на тяжелые и легкие. Легкими являются задачи, для которых возможно получить хорошее приближение для поиска корня. Тяжелые – это задачи, для которых такое приближение отсутствует (точка qi располагается вблизи поверхности разреза). Поверхность разреза находится с помощью аналитической функции Результаты работы программ Вычисление индивидуальной эластики. В таблице 1 приведены результаты типичного тестирования для 300 индивидуальных задач. Алгоритм демонстрирует хорошее распараллеливание для двух узлов (это объясняется спецификой решаемой системы уравнений), однако для большего числа узлов эффективность падает. Таблица 1
Вычисление серии эластик с использованием решения предыдущей задачи. В таблице 2 приведены показатели эффективности распараллеливания решения серии из 1000 задач для случая, когда имеется большое количество тяжелых задач. Использовался следующий закон изменения граничных условий эластики: q1(s)=(1/2cos(2ps), 1/2sin(2ps), 50ps), sÎ[0, 1]. Таблица 2
Таблица показывает высокую эффективность распараллеливания для рассматриваемого класса задач.
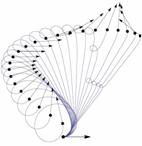
На рисунке приведены кадры анимаций, вычисленных с помощью созданных программ. (Анимации имеются в открытом доступе по адресу http://www.botik.ru/PSI/CPRC/sachkov/GROUP/ group.html). Алгоритмические и программные методы, разработанные для исследования эйлеровых эластик, находят применение в ряде других родственных задач (например, при восстановлении изображений на основе вариационного подхода и решении двухточечных задач управления с помощью нильпотентной аппроксимации). Литература 1. Эйлер Л. Метод нахождения кривых линий, обладающих свойствами максимума или минимума. Приложение I «Об упругих кривых». М.–Л.: ГТТИ, 1934. С. 447–572. 2. Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит, 2005. 3. Sachkov Yu.L. Maxwell strata in Euler's elastic problem, Journal of Dynamical and Control Systems. Vol. 14 (2008), № 2 (April), pp. 169–234. 4. Ардентов А.А., Сачков Ю.Л. Решение задачи Эйлера об эластиках // Автоматика и телемеханика. 2009. № 4. С. 78–88. 5. Wolfram S. Mathematica: a system for doing mathematics by computer, Addison-Wesley, Reading, MA 1991. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2375&lang=&lang=&like=1 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Параллельный программный комлекс оптимального развития динамической транспортной сети
- Параллельный программный комплекс решения неголономных задач управления
- Восстановление изображений на основе вариационного принципа
- Информационная среда проектирования систем ресурсосберегающего управления промышленным оборудованием
- О применении линейного программирования для повышения живучести АСУ технологическими процессами
Назад, к списку статей



 ,
, 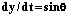 ,
,  ,
, , q(0)=(0,0,0),
, q(0)=(0,0,0),
 ,
,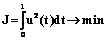 .
. записывается значение yn. Запускается поиск решения системы q(y)=q1 методом Ньютона с начальным значением
записывается значение yn. Запускается поиск решения системы q(y)=q1 методом Ньютона с начальным значением 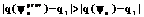 , то повторяются операции пункта 3, иначе переходим к пункту 1.
, то повторяются операции пункта 3, иначе переходим к пункту 1. . Сначала на узлы для вычисления рассылаются тяжелые задачи. Эти задачи решаются по схеме решения индивидуальной задачи. После того как узел решил задачу i, для следующей легкой задачи i+1 (если она не решена) создается начальное приближение для системы q(y)=q1, где q1 – корень, полученный в задаче i. Как только все тяжелые задачи решены, на вычисление рассылаются оставшиеся легкие задачи, для которых уже имеется начальное приближение. По мере решения легких задач создаются хорошие начальные приближения для оставшихся легких задач. Решение таких задач происходит с помощью метода Ньютона.
. Сначала на узлы для вычисления рассылаются тяжелые задачи. Эти задачи решаются по схеме решения индивидуальной задачи. После того как узел решил задачу i, для следующей легкой задачи i+1 (если она не решена) создается начальное приближение для системы q(y)=q1, где q1 – корень, полученный в задаче i. Как только все тяжелые задачи решены, на вычисление рассылаются оставшиеся легкие задачи, для которых уже имеется начальное приближение. По мере решения легких задач создаются хорошие начальные приближения для оставшихся легких задач. Решение таких задач происходит с помощью метода Ньютона.