Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Оптимизация элементов конструкции электрических соединителей
Аннотация:В статье рассматриваются преимущества использования специализированных программных модулей CAD-систем для решения задач проектирования. Описан разработанный автором статьи модуль САПР КОМПАС-3D, реализующий задачу условной оптимизации. Демонстрируется его работа на примере элемента электрического соединителя.
Abstract:There are advantages of using of specialized program modules of CAD systems to the decision of tasks of designing in article. Module of CAD system KOMPAS-3D developed by the author article is described. It realized a task of conditional optimization. Its work for an example of an element of an electric connector is demonstrated.
| Автор: Сафонов А.Л. (safonoval@yandex.ru) - Брянский государственный технический университет | |
| Ключевые слова: метод бокса, задача оптимизации, электрический соединитель, специализированный расчетный программный модуль, сапр |
|
| Keywords: Box method, optimization problem, electric connector, specialized engineering program module, CAD system |
|
| Количество просмотров: 11076 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Современная радиоэлектронная аппаратура – это сложнейшие многофункциональные изделия, которые состоят из огромного количества радиоэлектронных компонентов, в том числе электрических соединителей, обеспечивающих соединение и коммутацию различных электрических цепей и систем аппаратуры. Такая аппаратура используется в сложнейших изделиях специального и общепромышленного применения (авионика, системы телекоммуникаций, ГЛОНАСС и др.). Успешное решение проблемы обеспечения высокого качества соединителей должно закладываться уже на стадии формирования идеи создания электрических соединителей с необходимым набором потребительских свойств и качеств, таких как функциональность, надежность, технологичность, экономическая целесообразность и пр. Решение подобной задачи на уровне современных требований с применением существующих методик и средств инструментального обеспечения крайне затруднительно и очень затратно. Сокращение сроков разработки высокотехнологичных наукоемких электрических соединителей мирового технико-экономического уровня, повышение эффективности затрат на их создание и при этом максимальное освобождение конструкторов от выполнения рутинных проектных операций при анализе различных конструкторских решений возможно лишь на основе автоматизации процесса проектирования. В САПР целесообразно использовать автоматизированные объектно-ориентированные системы проектирования – CAD-системы, адаптированные к конкретной предметной области с помощью программно-методических модулей. Применение специализированных модулей CAD-систем для совмещения проектных расчетов (в частности, многопараметрических задач оптимизации) с непосредственным проектированием позволяет сократить длительность цикла «проектирование–анализ–изменение» [1], а также количество натурных экспериментов. В данной статье описан разработанный автором программный модуль САПР КОМПАС-3D, реализующий задачу оптимизации параметров элемента электрического соединителя. Большое количество параметров конструкции электрических соединителей, влияющих на все возрастающие и часто альтернативные требования к показателям их качества, делает практически невозможной доводку элементов электрических соединителей традиционными методами. В качестве таких параметров могут выступать геометрические размеры или свойства материалов деталей и их покрытий. Так, для элементов электрических соединителей их изменение даже на незначительную величину может вызвать существенные изменения характеристик этих элементов и соединителя в целом. Поэтому создание инструментальных средств для решения задач оптимизации при проектировании электрических соединителей весьма актуально. При решении конкретной задачи оптимизации исследователь должен выбрать математический метод, который приводил бы к конечным результатам с наименьшими затратами на вычисления или же давал возможность получить наибольший объем информации об искомом решении. Выбор того или иного метода в значительной степени определяется постановкой оптимизационной задачи, а также используемой математической моделью объекта оптимизации. Для решения оптимальных задач применяется большое многообразие методов. В данной работе реализован комплексный метод Бокса, представляющий модификацию метода деформируемого многогранника и предназначенный для решения задачи нелинейного программирования с ограничениями-неравенствами. Для минимизации целевой функции n переменных f(x) в n-мерном пространстве строят многогранники, содержащие q>n+1 вершин. Эти многогранники называют комплексами, что и определило наименование метода. Достоинствами комплексного метода Бокса являются его простота, удобство и надежность. Метод на каждом шаге использует информацию только о значениях целевой функции и функций ограничений задачи. Все это обусловливает его успешное применение для решения различных задач нелинейного программирования. Метод широко освещен в литературе, в частности, его алгоритм приведен в [2]. На основе данного метода оптимизации создан программный модуль, реализованный в качестве прикладной библиотеки САПР КОМПАС-3D и использующий API-интерфейс доступа к данным документа. Объектом параметризации является модель активного 3D-документа. Модуль работает как средство вычисления параметров, визуализация же осуществляется непосредственно самой САПР КОМПАС-3D. После запуска модуля необходимо задать данные для оптимизации. Прежде всего это список переменных модели для использования в качестве параметров оптимизации. Параметрическая модель детали должна быть построена так, чтобы все конструктивные параметры зависели от выбранных переменных, то есть модель могла бы быть полностью и правильно переопределена при изменении этих переменных. В качестве параметров оптимизации могут выступать не только конструктивные размеры, но и другие величины, например, характеристики материалов, массы компонентов. В этом случае такая переменная должна быть искусственно добавлена в список переменных модели, а остальные параметры могут рассчитываться исходя из ее величины. Как уже отмечалось, из списка, который подгружает переменные модели, можно последовательно выбрать переменные, указав область их определения – линейные ограничения на параметры. Тут же существует возможность задать весовой коэффициент параметра (при отсутствии задания целевой функции, описанной ниже, используется целевая функция по умолчанию). После выбора они отображаются в окне модуля Список параметров, где показывается их текущее числовое значение. Необходимо отметить невозможность повторного добавления одной и той же переменной, что оправданно для задачи оптимизации. В данном случае рассмотрим задачу условной оптимизации, то есть возможность задания ограничений на вектор параметров оптимизации. В принципе, задание области определения параметров – тоже простейшие линейные ограничения. Но на практике оказывается, что только эти ограничения не могут удовлетворить проектировщика при решении задачи оптимизации реального проектного задания. Поэтому в разработанном программном модуле предусмотрено создание других видов ограничений. Первый вид условно назван ограничительными параметрами: созданные в документе КОМПАС-3D переменные, значения которых заданы каким-либо алгебраическим выражением, содержащим константы и другие переменные документа, могут выступать в роли ограничений. Переменная, выбранная из списка переменных проекта, получает лимитирующие значения (максимум и/или минимум). При поиске оптимального значения целевой функции эти параметры с лимитирующими значениями используются в соответствии с алгоритмом, описанным выше. Однако для выполнения всех целей разрабатываемого модуля одних алгебраических ограничений недостаточно. Часто при проектировании каких-либо изделий возникает необходимость в более сложных ограничениях, которые могут включать в себя оператор условия или циклические алгоритмы. Для этих целей в программном модуле оптимизации предусмотрена возможность создания ограничений, условно названных автором ограничивающими функциями. Для создания такого ограничения следует нажать в модуле соответствующую кнопку, после чего внести необходимые данные по ограничению, а именно, название ограничения, ограничивающие значения (максимум, минимум либо оба значения) и файл, содержащий тело функции. Можно указать существующий файл или создать новый. Структура данного файла должна соответствовать синтаксису языка программирования Си и содержать лишь тело одной функции. В нем можно использовать выражения, функции, директивы, операторы, что позволяет реализовать достаточно сложные алгоритмы, которые нельзя или проблематично выполнить при помощи ограничительных параметров (алгебраических выражений, содержащих переменные документа). В этом файле также можно использовать переменные документа или объявлять новые. Как уже отмечалось, возможно использование операторов цикла и условия. После определения файла необходимо провести его компиляцию в программный код динамической библиотеки. Для этого нажимается кнопка «Читать файл». В модуль входит простейший консольный компилятор программного кода cl.exe, поэтому дополнительное программное обеспечение для создания dll-библиотеки не требуется. Если файл с исходным кодом не содержит синтаксических ошибок, пользователь не получит сообщение о них, и для завершения создания ограничивающей функции нужно подтвердить информацию. При вызове функции (на каждой итерации поиска оптимального решения) значения переменных проекта будут обновляться в dll-библиотеках ограничивающих функций, что позволяет получать ее актуальное значение при каждом вызове. Для полного описания задачи оптимизации остается только описать целевую функцию. Технически это реализуется аналогично определению ограничивающих функций, для чего используется механизм dll-библиотек. Кроме того, указывается файл с исходным кодом на языке программирования Си. Описывается алгоритм определения целевой функции согласно правилам языка, при этом возможно обращение к любым переменным документа проекта. В программном коде файла ограничивающей функции можно использовать операторы и функции языка Си. Однако само определение целевой функции – задача нетривиальная. Из всего многообразия характеристик изделия необходимо выбрать наиболее значимые и сформулировать алгоритм получения лишь одного значения, наиболее точно характеризующего объект исследования. К решению этой сложной задачи проектировщик должен подойти творчески, быть компетентным в своей области. Можно подключить к работе экспертов для определения с их помощью возможных целевых функций и ограничений проекта. Для демонстрации работы модуля и творческого решения задачи проектирования рассмотрим поиск оптимального решения для вилочного контакта электрического соединителя. За первоначальную точку принималась конструкция существующего контакта. Было решено, что параметрами оптимизации станут три конструктивных размера – длина, ширина контакта и толщина материала, из которого выполнена деталь. В САПР КОМПАС-3D ее параметрическая модель была выполнена таким образом, что конструкция модели полностью и без ошибок определялась по этим трем параметрам (все размеры определены константами или выражениями, значения которых однозначно вычисляются исходя из значений параметров оптимизации). Далее были наложены ограничения на проектируемую систему. В список ограничительных параметров добавлены три переменные. Их значение определяется выражениями, смысл которых заключается в запрете на появление вырожденных объектов (появление отрицательных размеров, отдельных частей детали и т.п.). В качестве ограничительных функций использованы электрическое сопротивление контакта и усилие расчленения контакта [3]. На практике необходимо обеспечить значение сопротивления не больше оговоренной в техническом задании величины и значение усилия расчленения контактов, лежащего в определенных пределах (иначе при малом его значении возможно нарушение контактирования, а при большом усилии возможны деформация контактов и поломка соединителя). При этом считается, что известна толщина рабочей части вилочного контакта. Обе характеристики (сопротивление контакта и усилие расчленения контакта) зависят от жесткостных характеристик контакта, обеспечивающих силу контактирования рабочих частей контактов. Для задания ограничивающих функций были созданы файлы, содержащие написанный на языке программирования Си исходный код тела функций. После этого выполнена компиляция исходного текста в динамическую библиотеку. Также были заданы ограничивающие значения (для сопротивления – максимальное, для усилия сочленения/расчленения – максимальное и минимальное). Конечно, в данном случае приведен лишь пример использования модуля, а поиск и формулирование зависимостей характеристик изделия от конструктивных параметров выходят за рамки этой работы. В качестве целевой функции рассматривалось несколько вариантов: минимальность габаритов, массы контактов, площади покрытия драгоценными металлами. Можно принять комбинацию нескольких функций оптимизации с весовыми коэффициентами. Для простоты использовалась следующая функция: F(X1, X2, X3)=0,95´X1+0,02´X2+ +0,03´X3, где X1 – толщина материала, из которого изготовляют контакт (толщина большинства частей контакта), мм; X2 – длина контакта, мм; X3 – ширина контакта, мм. Коэффициенты при параметрах в выражении целевой функции характеризуют степень важности каждого из них и относительность их размеров. Далее, как и для ограничивающих функций, составляется файл с исходным кодом тела функции, проводится компиляция его в dll-библиотеку, после чего программный модуль будет обращаться к ней на каждом шаге итерации при поиске оптимального значения.
Достоинством данного метода является управляемость процессом оптимизации. На каждом шаге возможна визуализация результата – представление трехмерной модели КОМПАС-3D, что позволяет проектировщику анализировать результат, вносить определенные поправки. Использование внешних программных модулей САПР является мощным средством для повышения производительности и качества работы. Важнейшим преимуществом применения таких разработок является использование существующей на предприятии САПР как базовой, без приобретения дополнительных специализированных пакетов для компьютерного моделирования. В частности, разработанный автором программный модуль САПР КОМПАС-3D позволяет решать важную задачу проектирования – поиск оптимальных параметров, ограничиваясь возможностями базовой версии САПР КОМПАС-3D. В работе демонстрируются лишь принципы работы модуля, решение же реальных задач производства намеренно остается нераскрытым. Литература 1. Ли К. Основы САПР (CAD/CAM/CAE). СПб. Питер, 2004. 560 с. 2. Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения. URL: http://matlab.exponenta.ru/optimiz/book_2/index.php (дата обращения: 18.03.2009). 3. Сафонов Л.И., Сафонов А.Л. Прямоугольные электрические соединители. Анализ физических процессов, происходящих в контакте // Технологии в электронной промышленности. 2007. № 6. С. 54–58. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2388 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программная реализация адаптивной компонентной автоматизированной обучающей системы
- Архитектура инструментальной среды для обработки проектных процедур, представленных в функционально адаптируемой форме
- Комплекс программ оптимизации компоновки объектов химических производств
- Генетический алгоритм проектирования основных переходов в САПР технологических процессов ковки валов
- Лингвистическое обеспечение САПР технологии ковки валов на прессах
Назад, к списку статей



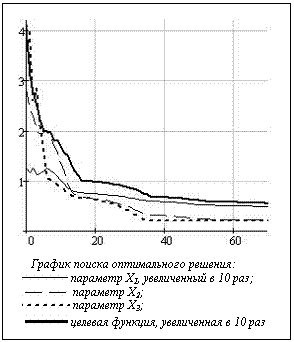 Перейдем непосредственно к поиску оптимальных значений параметров. Это итерационная процедура, заканчивающаяся в случае, если изменение целевой функции за пять циклов не превысит определенного малого значения. На рисунке отображен результат хода выполнения поиска оптимальных значений. Сплошной толстой линией на графике показана величина целевой функции, а другими линиями – значения параметров оптимизации. По оси абсцисс отложены шаги итерации, а по оси ординат – значения величин целевой функции и параметров оптимизации (для наглядности приведены в соответствующих масштабах).
Перейдем непосредственно к поиску оптимальных значений параметров. Это итерационная процедура, заканчивающаяся в случае, если изменение целевой функции за пять циклов не превысит определенного малого значения. На рисунке отображен результат хода выполнения поиска оптимальных значений. Сплошной толстой линией на графике показана величина целевой функции, а другими линиями – значения параметров оптимизации. По оси абсцисс отложены шаги итерации, а по оси ординат – значения величин целевой функции и параметров оптимизации (для наглядности приведены в соответствующих масштабах).