Авторитетность издания
Добавить в закладки
Следующий номер на сайте
HeО: библиотека метаэвристик для задач дискретной оптимизации
Аннотация:В статье рассматривается новая библиотека метаэвристических алгоритмов HeO для решения трудных задач дискретной оптимизации. Библиотека представляет собой набор алгоритмических каркасов, выполненных с использованием современных технологий программирования, метапрограммирования и параллельных вычислений. Приведены результаты тестирования библиотеки на задачах выполнимости из наборов SAT 2007 и SAT 2009.
Abstract:In the present paper we introduce HeO, a new software library of metaheuristic algorithms for hard combinatorial optimization problems. The library is designed as a set of algorithmic skeletons implemented using modern programming, metaprogramming and parallel computing techniques. The results of efficiency testing over SAT problems from the SAT 2007 and SAT 2009 sets are provided.
| Авторы: Цыганов А.В. (andrew.tsyganov@gmail.com) - Ульяновский государственный педагогический университет им. И.Н. Ульянова (профессор), Ульяновск, Россия, кандидат физико-математических наук, Булычов О.И. (oleg.bulychov@gmail.com) - Ульяновский государственный педагогический университет | |
| Ключевые слова: openmp, mpi, параллельные вычисления, алгоритмические каркасы, метаэвристики, дискретная оптимизация |
|
| Keywords: OpenMP, MPI, parallel computing, algorithmic skeletons, metaheuristics, combinatorial optimization |
|
| Количество просмотров: 11926 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
Метаэвристические алгоритмы уже несколько десятилетий с успехом применяются для решения трудных задач дискретной оптимизации (ЗДО). Их популярность вызвана рядом причин, основными из которых являются: - простота и ясность концепций, лежащих в основе, что обусловливает относительно несложную реализацию; - высокий уровень абстракции, позволяющий использовать данные алгоритмы для решения широкого круга задач; - возможность гибридизации и распараллеливания, что позволяет на основе базовых алгоритмов получать новые, более эффективные методы оптимизации. На сегодняшний день разработано большое количество программных средств, в которых реализованы те или иные метаэвристические алгоритмы для решения конкретных ЗДО. В последние годы наметилась тенденция создания универсальных библиотек (frameworks) [1], применяемых для решения самых разнообразных задач. В настоящей статье рассматривается библиотека метаэвристических алгоритмов HeO (Heuristic Optimization), разработанная авторами с использованием современных технологий программирования, метапрограммирования и параллельных вычислений на языке C++. Основные особенности библиотеки Библиотека HeO является проектом с открытым исходным кодом и распространяется на основе лицензии MIT. Цель проекта – обеспечить исследователей современными и простыми в использовании средствами для решения широкого круга ЗДО. Ключевыми особенностями библиотеки являются: · кроссплатформенность, обеспечивающая возможность компиляции программ в операционных системах Windows и Linux без изменения исходного кода; · поддержка архитектур x86 и x64; · реализация методов оптимизации в виде алгоритмических каркасов; · реализация каждого метода оптимизации с использованием двух технологий параллельного программирования: MPI и OpenMP; · использование оригинальной обертки (wrapper) для функций MPI; · использование оригинальной технологии отражения (reflection), позволяющей организовать унифицированный подход к загрузке, сохранению, выводу на экран и передаче экземпляров классов по сети; · наличие мастеров (wizards), облегчающих создание пользовательских проектов; · прозрачность параллелизма для пользователей библиотеки. Официальная страница проекта располагается по адресу http://www.code.google.com/p/heo. В настоящее время для скачивания доступна версия 1.0 библиотеки. Архитектура библиотеки Содержимое библиотеки распределено по семи основным каталогам: 1) contrib – библиотеки и файлы сторонних разработчиков, не являющиеся частью проекта; 2) doc – файлы документации; 3) logins – логины и пароли пользователей (для запуска MPI-приложений); 4) problems – входные файлы задач; 5) projects – проекты пользователей и демонстрационные проекты; 6) solvers – исходные файлы реализованных в библиотеке методов оптимизации; 7) src – исходные файлы вспомогательных классов. В каждом каталоге могут содержаться подкаталоги, соответствующие различным задачам, проектам, методам и т.п. Библиотека представляет собой набор классов, которые можно разделить на две большие группы – основные и вспомогательные классы. Основные классы участвуют в непосредственной реализации того или иного метода оптимизации. Их исходный код хранится в каталоге solvers. Вспомогательные классы выполняют различные служебные функции. Их исходный код хранится в каталоге src. В библиотеке реализованы два метода оптимизации: генетический алгоритм (GA – Genetic Algorithm) и метод имитации отжига (SA – Simulated Annealing) [2]. Ядро основных классов библиотеки составляют так называемые решатели (solvers). Каждый решатель выполнен в виде отдельного шаблона класса и реализует конкретный метод оптимизации в соответствии с определенной технологией параллельного программирования (MPI или OpenMP). На данный момент в библиотеке имеются четыре решателя (по два на каждый метод оптимизации). Название каждого решателя состоит из двух частей, разделенных символом подчеркивания. Первая часть – это сокращенное название метода оптимизации (например GA). Вторая часть – сокращенное название технологии параллельного программирования (например OMP). Таким образом, GA_OMP соответствует решателю, в котором реализована OpenMP-версия генетического алгоритма, а SA_MPI – решателю, в котором реализована MPI-версия метода имитации отжига. Исходный код решателей для одного и того же метода оптимизации хранится в каталоге solvers/<имя метода> в следующих файлах: <имя_метода>_common.h – исходный код, общий для всех решателей; <имя_метода>_mpi.h – исходный код MPI-решателя; <имя_метода>_omp.h – исходный код OpenMP-решателя. Например, исходный код решателей для генетического алгоритма хранится в каталоге sol- vers/ga в файлах ga_common.h, ga_mpi.h и ga_omp.h соответственно. Кроме решателей, к основным классам, исходные коды которых хранятся в каталоге solvers, относятся также конфигурационные классы. Каждый такой класс позволяет управлять работой решателей, относящихся к одному и тому же методу оптимизации, а его исходный код хранится в том же каталоге, что и исходный код самих решателей в файле <имя метода>_config.h (например, ga_config.h). Управление ходом вычислений осуществляется посредством конфигурационных файлов, данные в которых хранятся в формате параметр = значение. По умолчанию конфигурационные файлы имеют расширение *.ini. Решатели выполнены в соответствии с идеологией алгоритмических каркасов. Это означает, что в них реализована только проблемно-независимая часть алгоритма, а также скрыты все аспекты параллельной реализации. Эти особенности позволяют применять решатели к широкому кругу задач и делают параллелизм прозрачным для пользователя. Приведем пример объявления шаблона класса для решателя GA_OMP: template class GA_OMP ... Для использования решателя необходимо заменить параметры его шаблона (P, S и C) тремя классами. Первые два класса реализуются пользователем и описывают свойства решаемой задачи и ее допустимых решений соответственно. В данных классах обязательно должны быть реализованы методы, специфичные для выбранного алгоритма оптимизации (например, методов рекомбинации и мутации для генетического алгоритма). Третий класс является конфигурационным, он наследует свойства проблемно-зависимого конфигурационного класса (реализуется пользователем) и проблемно-независимого конфигурационного класса (реализован в библиотеке). В библиотеке имеются средства автоматизации создания проектов пользователя под Windows и Linux − так называемые мастера (wizards), что существенно облегчает использование данной библиотеки по сравнению с имеющимся аналогичным программным обеспечением. Мастера избавляют пользователя от необходимости досконального изучения всех особенностей библиотеки и позволяют сконцентрировать усилия на разработке проблемно-зависимых классов. Для того чтобы применить решатель к нужной ЗДО, пользователю обычно требуется выполнить серию стандартных действий: проанализировать параметры командной строки, считать конфигурационный и входной файлы задачи, инициализировать решатель, запустить вычисления, вывести результат и т.д. Для выполнения этой рутинной процедуры в библиотеке реализованы два вспомогательных шаблона класса: Run_MPI и Run_OMP. Приведем пример объявления шаблона класса Run_MPI: template class Run_MPI... Для запуска вычислений пользователь должен заменить параметр S в данном шаблоне на нужный решатель и вызвать метод run(). Более подробная информация об архитектуре и особенностях использования библиотеки содержится в документации (каталог doc). Для демонстрации возможностей библиотеки были разработаны проекты для операционных систем Windows и Linux, в которых реализованы проблемно-зависимые классы для задач ONE-MAX и MAX-SAT и использованы все имеющиеся в библиотеке решатели. Исходные коды этих проектов хранятся в каталоге projects, а входные файлы задач – в каталоге problems. Тестовая конфигурация и методика тестирования Тестирование эффективности реализованных в библиотеке методов оптимизации проводилось на примере задач выполнимости (SAT) больших размерностей из наборов SAT 2007 и SAT 2009, доступных на сайте http://www.satcompetition.org. Задачу выполнимости можно кратко сформулировать следующим образом: дана конъюнктивная нормальная форма функции N переменных из M клауз. Необходимо определить, существует ли двоичный набор, при котором эта функция будет выполнима (то есть значения всех ее клауз будут равны 1). Клаузы могут быть как фиксированной, так и переменной длины. Описание различных формулировок задач SAT и MAX-SAT можно найти, например, в [3]. Тестирование библиотеки проводилось на двух системах. Первая представляла собой однородный кластер (систему с распределенной памятью). Ее аппаратно-программная конфигурация: количество машин – 20; процессоры – Intel Core 2 Duo E7200 @ 2.53 ГГц; ОЗУ – 2 Гб; сеть – 100 Мбит Ethernet; операционная система – Linux 2.6.25-gentoo-r7; библиотека MPI – LAM 7.1.2. Вторая являлась системой с общей памятью. Аппаратно-программная конфигурация ее следующая: процессор – Intel Core 2 Quad Q6600 @ 2.4 ГГц; ОЗУ – 4 Гб; операционная система – MS Windows XP Professional SP 2; библиотека MPI – MPICH2 1.0.8. Методика тестирования состояла в следующем. Для решения выбирались только выполнимые задачи больших размерностей. На первой системе каждая задача поочередно решалась с помощью решателей GA_MPI и SA_MPI с числом потоков 1, 2, 4, 8, 16, 32. Для второй системы использовались все четыре решателя (GA_OMP, GA_MPI, SA_OMP, SA_MPI) с числом потоков 1, 2, 3, 4. Для каждого запуска запоминались время выполнения и число невыполненных клауз. В таблице 1 приведены основные настройки решателей для обоих методов. Перед рассмотрением результатов тестирования заметим, что в решателе GA_MPI реализована островная модель (island model) генетического алгоритма, а в решателях SA_MPI и SA_OMP – мультистартовая модель (multi-start model) метода имитации отжига. В этих моделях поиск решения осуществляется всеми потоками независимо, с периодической кооперацией (обменом результатами). Такая стратегия позволяет с увеличением числа потоков увеличивать точность получаемого решения (ускорять сходимость), но ускорения вычислений при этом не происходит. Кроме того, в этих решателях реализованы два режима работы – асинхронный и синхронный. Использование асинхронного режима позволяет избежать временных задержек, связанных с синхронизацией при кооперации потоков, но приводит к тому, что при последовательных запусках с одними теми же настройками результаты решения могут оказаться разными. Таблица 1
В решателе GA_OMP реализована модель одной популяции, с которой одновременно работают все потоки (global population model). Данная модель позволяет ускорить время вычислений, но точность решения при этом не увеличивается. Результаты тестирования Приведем результаты тестирования для задачи ndhf_xits_20_SAT из набора SAT 2009. Параметры задачи: число переменных – 4242, число клауз – 503783. Результаты тестирования для системы с распределенной памятью приведены в таблице 2, где N – число потоков; ε – число невыполненных клауз; Δ – процент невыполненных клауз; t – время решения (сек.). Таблица 2
Из таблицы видно, что точность решения с увеличением числа потоков возрастает и вполне приемлема для универсальных методов. Результаты тестирования для решателей GA_MPI, SA_MPI и SA_OMP в системе с общей памятью оказались аналогичными приведенным выше. Исключением является решатель GA_OMP. Результаты тестирования для этого решателя приведены в таблице 3, где N – число потоков; ε – число невыполненных клауз; Δ – процент невыполненных клауз; t – время решения (сек.). Таблица 3
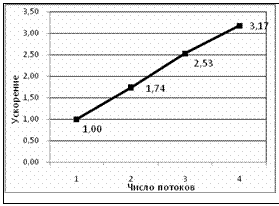
Из таблицы 3 видно, что с увеличением числа потоков увеличивается не точность, а скорость решения. График ускорения для решателя GA_OMP приведен на рисунке.
В ближайшей перспективе разработчики добавят в библиотеку новые методы оптимизации, в частности, метод поиска с переменной глубиной (VDS – Variable Depth Search), а также гибридные методы (прежде всего GA+SA). Кроме того, в следующих версиях библиотеки планируется реализация уже имеющихся методов оптимизации с использованием еще одной технологии параллельного программирования – Intel Threading Building Blocks (TBB). Литература 1. Цыганов А.В., Булычов О.И., Лавыгин Д.С. Исследование эффективности библиотеки MaLLBa на примере задач максимальной выполнимости // Программные продукты и системы. 2009. № 3. С. 116–120. 2. Handbook of metaheuristics / Ed. by F. Glover, G.A. Kohenberger. Kluwer Academic Publishers, 2003. 3. Hromkovič J. Algorithmics for hard problems. Introduction to combinatorial optimization, randomization, approximation, and heuristics. 2nd edition. Springer, 2004. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2400 |
Версия для печати Выпуск в формате PDF (4.85Мб) |
| Статья опубликована в выпуске журнала № 4 за 2009 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Исследование эффективности библиотеки MaLLBa на примере задач максимальной выполнимости
- Исследование статистических свойств алгоритмов минимизации недетерминированных конечных автоматов с использованием программы ReFaM
- Использование библиотеки MPI для параллельной реализации алгоритма полного перебора вариантов
- Генетический алгоритм для задачи вершинной минимизации недетерминированных конечных автоматов
- Система моделирования масс-спектрометра на основе параллельного кода частиц в ячейке
Назад, к списку статей



 В заключение следует отметить, что проведенное тестирование показало удобство использования библиотеки и эффективность реализованных методов.
В заключение следует отметить, что проведенное тестирование показало удобство использования библиотеки и эффективность реализованных методов.