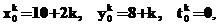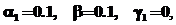Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Реализация вычислений на графическом процессоре с использованием платформы NVIDIA CUDA
Аннотация:Продемонстрирован подход к организации вычислений на графическом процессоре с помощью платформы NVIDIA CUDA. В результате вычислительного эксперимента по реализации численного метода решения системы обыкновенных дифференциальных уравнений получены более высокие показатели производительности графического процессора по сравнению с центральным процессором.
Abstract:The approach to an implementation of computing on the graphic processor units under platform NVIDIA CUDA is demonstrated. The results of numerical simulation of the system of ordinary differential equation show higher speed of computing on GPU as compared to CPU.
| Авторы: Белозёров А.С. (asbelozerov@gmail.com) - Омский государственный университет им. Ф.М. Достоевского, Коробицын В.В. (korobits@rambler.ru) - Омский государственный университет им. Ф.М. Достоевского, кандидат физико-математических наук | |
| Ключевые слова: методы рунге–кутты, вычисления на графическом процессоре, высокопроизводительные вычисления |
|
| Keywords: Runge–Kutta methods, computing on GPU, high-performance computing |
|
| Количество просмотров: 13349 |
Версия для печати Выпуск в формате PDF (4.03Мб) Скачать обложку в формате PDF (1.25Мб) |
Системы обыкновенных дифференциальных уравнений используются для описания большого класса математических моделей. Анализ таких моделей зачастую производится численно. С ростом количества уравнений в системе увеличиваются вычислительные затраты на построение траекторий решений. Для построения фазовых портретов и анализа бифуркаций необходимо многократно вычислять решения системы при разных значениях параметров и начальных данных системы. Возникает потребность в быстром вычислении большого количества траекторий. Такая вычислительная задача хорошо поддается распараллеливанию. Однако существует несколько принципиально разных подходов к организации параллельных вычислений: на центральном процессоре в многопоточном режиме, на параллельном компьютере с общей памятью, на вычислительном кластере, на графическом процессоре. Последний вариант реализации представляется наиболее интересным. Производительность современных графических процессоров (GPU) в вычислительных задачах превосходит производительность современных центральных процессоров (CPU), но при этом их стоимость сопоставима. Это преимущество используется для решения различных вычислительных задач в рамках направления GPGPU – задачи общего назначения для GPU (см. http://www.gpgpu.ru/). С помощью графических библиотек OpenGL и DirectX создаются программы-шейдеры для обеспечения вычислений на графическом процессоре. Однако данный путь предполагает определение задачи в терминах вершин, примитивов и текстур, принятых для GPU, с чем связаны накладные расходы, а также трудности с доступом к памяти из пиксельных, вершинных и геометрических программ. Платформа NVIDIA CUDA скрывает многие недостатки подхода непосредственного построения программ-шейдеров, предоставляя разработчику прямой доступ к ресурсам GPU, удобный программный интерфейс для параллельных вычислений и компилятор для языка C. Данная статья посвящена изучению способа реализации численного метода решения систем обыкновенных дифференциальных уравнений на платформе NVIDIA CUDA. Особенности реализации алгоритмов на платформе NVIDIA CUDA При программировании на CUDA используется следующая модель вычислений. С точки зрения программиста, GPU является сопроцессором для CPU, имеющим собственную память и способным параллельно выполнять огромное количество потоков. Параллельные участки выполняются на GPU в виде ядер (kernel), запускающихся одновременно в большом количестве потоков. Потоки (threads) группируются в блоки (blocks), которые объединяются в сетку (grid). Потоки внутри одного блока могут взаимодействовать между собой. Организация доступа к памяти графического процессора многослойна. Потоки имеют доступ на чтение и запись к регистрам, локальной памяти, разделяемой памяти блока и глобальной памяти сетки, а также доступ на чтение из текстурной и константной памяти сетки. Разные типы памяти имеют различное время доступа, поэтому эффективная реализация должна учитывать эту особенность организации графического процессора. Центральный процессор имеет доступ только к глобальной, текстурной и константной памяти сетки. Поэтому исходные данные задачи помещаются в эти типы памяти, а результаты вычислений должны быть перенесены из потоков в глобальную память сетки и далее на центральный процессор. Для компиляции CUDA-приложений используется компилятор NVCC [1]. Расширения для языка C подразделяются на четыре группы: · спецификаторы типов функций, указывающие, где будет выполняться функция (на CPU или GPU) и откуда она может быть вызвана; · спецификаторы типов переменных для уточнения, в какой области памяти (constant, device, global) будет располагаться переменная; · директива для уточнения, каким образом ядро должно запуститься на GPU; · встроенные переменные для обозначения размеров сетки и блоков, индексов потоков внутри сетки и блока. Запуск потока на выполнение и его конфигурацию опишем следующим образом: _global_ void KernelFunc(...); dim3 DimGrid(100, 50); // размер сетки dim3 DimBlock(4, 8, 8); // размер блока KernelFunc<<>>(...); // Запустить ядро Для выделения и освобождения памяти на GPU используют функции cudaMalloc() и cudaFree(); для выделения и освобождения на CPU – cudaMallocHost() и cudaFreeHost(). Копирование данных осуществляется с помощью функции cudaMemcpy(). Приведем пример программы на CUDA, осуществляющей вычисление простейшего арифметического выражения на графическом процессоре: int num=5; // Ядро, выполняемое на GPU _global_ void myKernelFunc (int* a) { int c = a * 2; } // Программа, выполняемая на CPU int main(void) { CUT_DEVICE_INIT(); // Инициализация int* A,devA; A=# // Выделение памяти cudaMalloc((void**)&devA, sizeof(int)); cudaMemcpy(devA,(void*)(&A),sizeof(int), cudaMemcpyHostToDevice); // Запуск ядра myKernelFunc<<<1,dim3(300,1)>>>(devA); cudaFree(devA); return 0; } Сравнение производительности GPU и CPU Оценка производительности вычислений на GPU и CPU производилась на известной системе уравнений Лотки–Вольтерра, так называемой модели «хищник–жертва»:
В эксперименте в каждом потоке производится вычисление траектории системы уравнений, имеющей одинаковые параметры, но отличающейся начальными данными:
здесь x0k, y0k – начальная точка траектории решения в момент tk0 потока с номером k. Используемые значения параметров системы:
Условия остановки процесса решения одинаковы для всех потоков: достигнуто заданное количество шагов N. Локальная точность решения выбрана невысокой, e=0.001, поскольку CUDA поддерживает только 32-битный формат чисел с плавающей точкой. В алгоритме использова- на вложенная схема Мерсона, обеспечивающая оценку локальной погрешности решения, и процедура автоматического выбора шага интегрирования. Численная имитация представленной модели была реализована в двух вариантах: в первом случае вычисления проводились на центральном процессоре, а во втором – на графическом. В таблице приведены результаты вычислительного эксперимента для сравнения производительности двух реализаций. Была исследована эффективность на длинных (10000 шагов) и коротких (500 шагов) решениях. Реализация метода Мерсона на CUDA демонстрирует очень высокую производительность по сравнению с CPU и отличную масштабируемость при увеличении количества траекторий. При количестве траекторий более 256 реализация на CUDA при использовании видеокарты на базе 8800GT показывает 10–15-кратное преимущество перед реализацией на процессоре Intel Core 2 Duo E8200. Учитывая, что стоимость видеокарты и процессора примерно одинакова, покупка видеокарты для подобных расчетов является намного более выгодным приобретением. Сравнение показателей производительности реализаций
Проведенный эксперимент показал, что платформа NVIDIA CUDA является удачным выбором для выполнения распараллеливаемых вычислительных экспериментов, если не предъявляются высокие требования к точности результата. К недостаткам платформы можно отнести поддержку только 32-битных чисел с плавающей точкой, невозможность динамического выделения памяти на GPU, отсутствие поддержки рекурсии и указателей на функции, что ограничивает возможности приложений, реализуемых на CUDA. Возможности платформы были продемонстрированы при параллельном решении систем дифференциальных уравнений методом Мерсона. Реализация на CUDA показала значительный выигрыш в производительности по сравнению с тем же алгоритмом, выполняемым на центральном процессоре – до 10 раз при решении уравнений с большим количеством необходимых итераций. Литература 1. NVIDIA CUDA Programming Guide 1.1 URL: http://www.nvidia.com/object/cuda_develop.html (дата обращения: 01.04.2009). 2. Хайрер Э., Нёрсетт С., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Нежесткие задачи. М.: Мир, 1990. 512 с. 3. Pharr M., Randima F. GPU Gems 2: Programming Techniques for High-Performance Graphics and General-Purpose Computation. Addison-Wesley, 2005. 812 pp. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2429 |
Версия для печати Выпуск в формате PDF (4.03Мб) Скачать обложку в формате PDF (1.25Мб) |
| Статья опубликована в выпуске журнала № 1 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Выбор языка высокого уровня для реализации вычислительного приложения
- Применение машинного обучения для прогнозирования времени выполнения суперкомпьютерных заданий
- Методы и средства моделирования системы управления суперкомпьютерными заданиями
- Применение метода английского аукциона при планировании заданий с абсолютными приоритетами в распределенной вычислительной системе
- Выбор вычислительной системы для решения научных задач
Назад, к списку статей