Высокая твердость, дисперсность закаленной фазы и отсутствие на поверхности бочки валка волосовидности и микротрещин являются условиями получения холоднокатаного листового проката высокого качества. Окончательная термическая обработка является важнейшей и наиболее ответственной операцией в производстве рабочих валков холодной прокатки, обеспечивающей необходимый фазовый состав, распределение этих фаз по объему и допустимое распределение термических напряжений. Неправильный режим нагрева и закалки способствует выходу валка из строя иногда даже до начала эксплуатации.
Экспериментальные работы по выбору оптимальных режимов термообработки трудоемкие и дорогостоящие, так как каждый прокатный валок представляет собой уникальную деталь. Программный продукт «Тепловые процессы в прокатном валке при индукционном нагреве» позволяет посредством численного эксперимента подбирать рациональные режимы предварительной и окончательной термической обработки, которые обеспечивали бы получение валка требуемой твердости, но не приводили к его разрушению вследствие термонапряжений.
Объектом моделирования является прокатный валок или цилиндрическая деталь, подлежащая термической обработке. При определении температурного поля в валке при нагреве решалась двухмерная осесимметричная задача нестационарной теплопроводности и принимался ряд допущений и ограничений. Считалось, что рассматриваемые процессы нестационарные и температура существенно меняется вдоль осей r и z. Нагрев цилиндрического тела происходит при постоянном напряжении U на зажимах индуктора за счет наведения токов электромагнитной индукции в зоне действия индуктора. В тепловом отношении это эквивалентно действию внутренних источников теплоты qv(r, z, t), мощность которых в общем случае зависит от координат и времени. Охлаждение валка происходит с его боковой поверхности и торцов посредством вынужденной конвекции от воздуха, который набегает на вращающийся валок. В период закалки охлаждение происходит только с боковой поверхности валка посредством вынужденного движения струй воды.
Распределение температуры в рассматриваемой области описывается уравнением теплопроводности с учетом выделения тепла от индуктора:
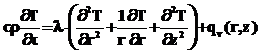 , (1)
, (1)
где qv – мощность внутренних источников тепла; с, ρ, λ – теплофизические свойства материала валка [1–3].
Для решения дифференциального уравнения (1) необходимо дополнить его краевыми условиями. При t=0, 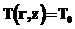 на оси цилиндра r=0, z=0,…,L имеем условие симметрии
на оси цилиндра r=0, z=0,…,L имеем условие симметрии  .
.
На боковой поверхности цилиндра z=0,...,L; r=R имеем охлаждение окружающим воздухом (граничное условие третьего рода):
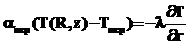 .
.
На торцевых поверхностях цилиндра теплоотдача в окружающую среду (граничные условия третьего рода):
– на левой границе Z=0, r=0,…,R:
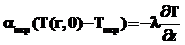 ;
;
– на правой границе Z=L, r=0,…,R:
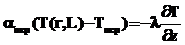 .
.
В зоне действия индуктора температура поверхности валка с учетом тепловыделения Z=Zn,…,Zk; r=R: 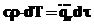 , где
, где 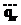 – среднее объемное тепловыделение в поверхностном слое.
– среднее объемное тепловыделение в поверхностном слое.
Охлаждение струями воды действует только при режиме закалки Z=Zжn,…,Zжk; r=R:
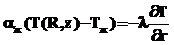 ,
,
где  – коэффициент теплоотдачи от струй воды; Zжn, Zжk – левая и правая границы зоны охлаждения.
– коэффициент теплоотдачи от струй воды; Zжn, Zжk – левая и правая границы зоны охлаждения.
 Мощность, передаваемая металлу, меняется во времени в связи с изменением физических свойств металла и его температуры. При расчете передаваемую мощность условно разбиваем на этапы: холодный (Px), промежуточный (Pп) и горячий (Pг). Холодный этап заканчивается, когда поверхность тела нагревается до температуры магнитных превращений Tk. Промежуточный этап соответствует наиболее резкому изменению магнитной проницаемости ферромагнетиков. Он начинается в момент достижения температуры магнитных превращений на поверхности валка и заканчивается, когда до этой температуры нагреваются точки, отстоящие от поверхности заготовки на глубину проникновения тока в горячий (немагнитный) материал – d. Далее нагрев осуществляется согласно горячему этапу.
Мощность, передаваемая металлу, меняется во времени в связи с изменением физических свойств металла и его температуры. При расчете передаваемую мощность условно разбиваем на этапы: холодный (Px), промежуточный (Pп) и горячий (Pг). Холодный этап заканчивается, когда поверхность тела нагревается до температуры магнитных превращений Tk. Промежуточный этап соответствует наиболее резкому изменению магнитной проницаемости ферромагнетиков. Он начинается в момент достижения температуры магнитных превращений на поверхности валка и заканчивается, когда до этой температуры нагреваются точки, отстоящие от поверхности заготовки на глубину проникновения тока в горячий (немагнитный) материал – d. Далее нагрев осуществляется согласно горячему этапу.
Для решения уравнения (1) использовался метод конечных разностей. На расчетную рабочую область накладывали прямоугольную сетку и использовали симметричную аппроксимацию пространственных производных. При численной реализации расчета использовался метод расщепления [4], приводящий к безусловно устойчивой локально-одномерной схеме.
Для цилиндрической стенки получим уравнение в виде трехдиагональной матрицы:
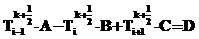 , (2)
, (2)
где  ;
; 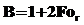 ;
; 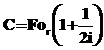 ;
;
 ;
; 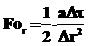 .
.
Для плоской стенки представим систему уравнений:
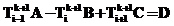 , (3)
, (3)
где 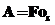 ;
; 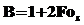 ;
; 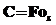 ;
;
 ;
; 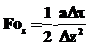 .
.
Каждая из систем уравнений (2–3) решалась методом прогонки.
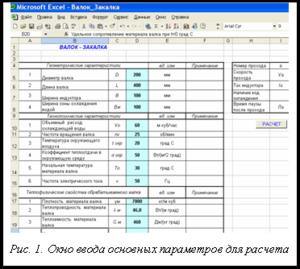
 В качестве исходных данных в программном продукте «Тепловые процессы в прокатном валке при индукционном нагреве» вводятся следующие технологические и теплофизические характеристики: диаметр и длина валка, плотность материала валка, теплопроводность, теплоемкость и др. Кроме того, учитываются геометрические размеры закалочной установки: диаметр и высота индуктора, ширина зоны охлаждения водой, коэффициент мощности индуктора, ток и напряжение на индукторе, диаметр сопла распылителя воды, число сопел распылителей воды, диаметр водяного коллектора.
В качестве исходных данных в программном продукте «Тепловые процессы в прокатном валке при индукционном нагреве» вводятся следующие технологические и теплофизические характеристики: диаметр и длина валка, плотность материала валка, теплопроводность, теплоемкость и др. Кроме того, учитываются геометрические размеры закалочной установки: диаметр и высота индуктора, ширина зоны охлаждения водой, коэффициент мощности индуктора, ток и напряжение на индукторе, диаметр сопла распылителя воды, число сопел распылителей воды, диаметр водяного коллектора.
Для реализации методов решения поставленной задачи была выбрана операционная система Windows (98/NT/2000/XP). Программирование осуществлялось в интегрированной среде разработки VBA for MS Office. Созданный программный продукт имеет удобный интерфейс и позволяет вводить и редактировать любые исходные данные, проверять их корректность и получать результаты в удобном табличном и графическом видах. Работа программы начинается с ввода основных геометрических и технологических характеристик. Далее задаются теплофизические и магнитные свойства стали обрабатываемого валка (рис. 1).
Перед запуском расчетов необходимо определить параметры расчетной сетки: шаг по времени, число интервалов сетки в расчетной области по диаметру и по длине валка.
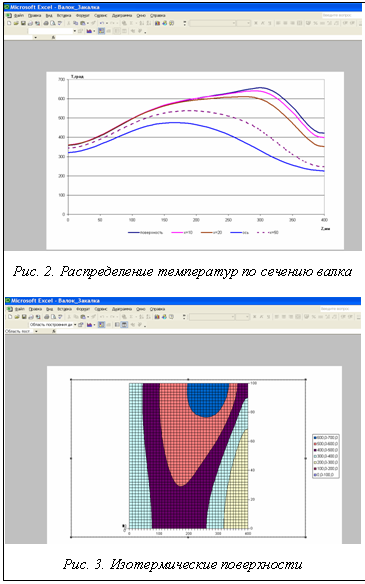
После расчета пользователь может просмотреть значения температуры в любой вертикальной и горизонтальной плоскости. На закладке «Распределение температур по сечению валка» можно просмотреть графическое отображение распределения температур на оси и поверхности валка, на заданных интервалах между ними за определенный интервал времени (рис. 2), а на закладке «Изотермические поверхности» – графическое отображение распределения температур по сечению валка (рис. 3) за заданный интервал времени.
Описанный программный продукт позволяет определять распределение нестационарных температурных полей в прокатном валке при индукционном нагреве токами различных частот двумя способами. Первый способ – одновременный нагрев, при котором индуктор охватывает всю поверхность детали, подлежащей термообработке. Второй – непрерывно-последовательный нагрев.
Программный продукт «Тепловые процессы в прокатном валке при индукционном нагреве» может использоваться для повышения технико-экономической эффективности работы действующих и проектируемых установок индукционного нагрева для термической обработки осесимметричных деталей машиностроения. Его применение поможет в подборе рациональных режимов как предварительной, так и окончательной термической обработки деталей без проведения дорогостоящих экспериментов. Кроме того, данный программный продукт может использоваться как инструмент в научно-исследовательской работе студентов старших курсов металловедческих специальностей, а также аспирантов и инженеров-исследователей.
Литература
1. Вдовин К.Н., Ячиков И.М., Егорова Л.Г. Модель температурного состояния прокатного валка при многопроходном индукционном нагреве под закалку // Математика. Приложение математики в экономических, технических и педагогических исследованиях: сб. науч. тр. Магнитогорск, 2005.
2. Вафин Р.К., Покровский А.М., Лешковцев В.Г. Прочность термообрабатываемых прокатных валков. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. 264 c.
3. Лабейш В.Г. Жидкостное охлаждение высокотемпературного металла. Л.: Изд-во ЛГУ, 1983. 172 с.
4. Яненко Н.Н. Метод дробных шагов решения многомерных задач математической физики. Новосибирск: Наука, 1967.



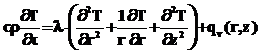 , (1)
, (1)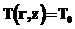 на оси цилиндра r=0, z=0,…,L имеем условие симметрии
на оси цилиндра r=0, z=0,…,L имеем условие симметрии  .
.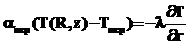 .
.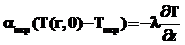 ;
;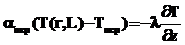 .
.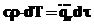 , где
, где 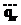 – среднее объемное тепловыделение в поверхностном слое.
– среднее объемное тепловыделение в поверхностном слое.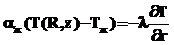 ,
, – коэффициент теплоотдачи от струй воды; Zжn, Zжk – левая и правая границы зоны охлаждения.
– коэффициент теплоотдачи от струй воды; Zжn, Zжk – левая и правая границы зоны охлаждения.
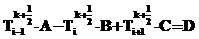 , (2)
, (2) ;
; 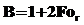 ;
; 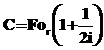 ;
; ;
; 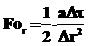 .
.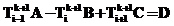 , (3)
, (3)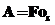 ;
; 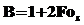 ;
; 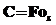 ;
; ;
; 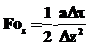 .
. В качестве исходных данных в программном продукте «Тепловые процессы в прокатном валке при индукционном нагреве» вводятся следующие технологические и теплофизические характеристики: диаметр и длина валка, плотность материала валка, теплопроводность, теплоемкость и др. Кроме того, учитываются геометрические размеры закалочной установки: диаметр и высота индуктора, ширина зоны охлаждения водой, коэффициент мощности индуктора, ток и напряжение на индукторе, диаметр сопла распылителя воды, число сопел распылителей воды, диаметр водяного коллектора.
В качестве исходных данных в программном продукте «Тепловые процессы в прокатном валке при индукционном нагреве» вводятся следующие технологические и теплофизические характеристики: диаметр и длина валка, плотность материала валка, теплопроводность, теплоемкость и др. Кроме того, учитываются геометрические размеры закалочной установки: диаметр и высота индуктора, ширина зоны охлаждения водой, коэффициент мощности индуктора, ток и напряжение на индукторе, диаметр сопла распылителя воды, число сопел распылителей воды, диаметр водяного коллектора.