Коэффициентные методики оценки объектов, основанные на получении интегрального (выходного) показателя суммированием оцениваемых частных (входных) показателей, умножаемых на соответствующие весовые коэффициенты [1], широко используются в практике оценки объектов, относящихся к самым разнообразным областям деятельности, так как обеспечивают рациональное сочетание оперативности получения результатов с возможностями их количественного обоснования.
Недостатком существующих компьютерных коэффициентных методик является отсутствие возможности реализации логических функций в процессе получения результата.
В [2] предложена компьютерно реализуемая методика оценки объектов с изменяемыми весовыми коэффициентами, в которой для весовых коэффициентов, умножаемых на соответствующие показатели, используются те или иные из заблаговременно устанавливаемых значений в зависимости от результата сравнения значения каждого показателя с соответствующим ему пороговым значением.
 Основным достоинством компьютерной методики оценки объектов с изменяемыми весовыми коэффициентами является возможность учета произвольных логических условий получения промежуточных и выходных показателей на основе реализации логических функций над характеризующими обрабатываемые входные и промежуточные показатели двоичными величинами.
Основным достоинством компьютерной методики оценки объектов с изменяемыми весовыми коэффициентами является возможность учета произвольных логических условий получения промежуточных и выходных показателей на основе реализации логических функций над характеризующими обрабатываемые входные и промежуточные показатели двоичными величинами.
Теоретические основы применения логических функций в компьютерных коэффициентных методиках
Рассмотрим обработку показателей, представленных вещественными числами. Для таких показателей при реализации логических функций можно ограничиться двоичными величинами  , характеризующими соотношение между значением показателя Хi и некоторой выбираемой величиной (a). Здесь Ä – один из знаков: =, >, <, ¹, £, ³. Возможные варианты проверяемых альтернативных условий приведеы в таблице.
, характеризующими соотношение между значением показателя Хi и некоторой выбираемой величиной (a). Здесь Ä – один из знаков: =, >, <, ¹, £, ³. Возможные варианты проверяемых альтернативных условий приведеы в таблице.
|
Функция
|
Условие
|
Двоичная величина
|
|
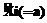
|
Хi=a
|
1
|
|
Хi¹a
|
0
|
|

|
Хi>a
|
1
|
|
Хi£a
|
0
|
|
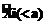
|
Хi
|
1
|
|
Хi³a
|
0
|
|
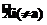
|
Хi¹a
|
1
|
|
Хi=a
|
0
|
|

|
Хi£a
|
1
|
|
Хi>a
|
0
|
|

|
Хi³a
|
1
|
|
Хi
|
0
|
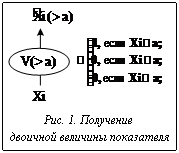
На приводимых рисунках, поясняющих реализацию логических функций в компьютерных коэффициентных методиках с изменяемыми весовыми коэффициентами, операция суммирования рассматриваемых величин обозначается прямоугольником с символом Σ, а операция умножения на весовой коэффициент – овалом с символическим обозначением весового коэффициента.
В качестве примера на рисунке 1 иллюстрируется преобразование (соответствующее 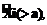 см. табл.) с использованием изменяемого весового коэффициента V(>a) значения обрабатываемого показателя Хi в двоичную величину
см. табл.) с использованием изменяемого весового коэффициента V(>a) значения обрабатываемого показателя Хi в двоичную величину 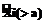 .
.
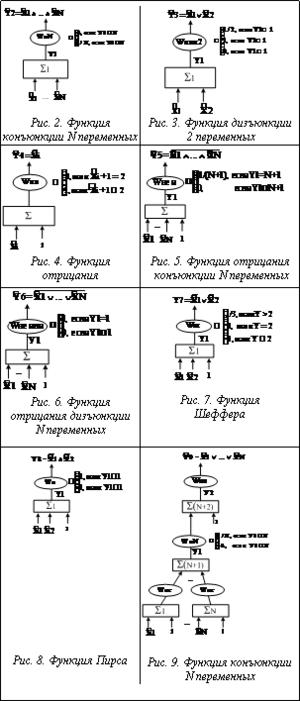
С использованием одного изменяемого весового коэффициента можно реализовать логические функции конъюнкции N переменных и дизъюнкции, но лишь двух переменных, а с прибавлением дополнительной единицы – также функции отрицания, функции отрицания конъюнкции и дизъюнкции N переменных, функции Шеффера и Пирса для двух переменных (рис. 2–8).
Фрагмент, реализующий функцию дизъюнкции N переменных, не удается реализовать с одним весовым коэффициентом, но можно это сделать, например, с использованием N+2 весовых коэффициентов, как это показано на рисунке 9.
Так как дизъюнкция, конъюнкция и отрицание образуют функционально полную систему логических функций, в компьютерных коэффициентных методиках оценки объектов с изменяемыми весовыми коэффициентами возможен учет любых логических условий оценки.
 Пример практического использования логических функций
Пример практического использования логических функций
Использование логических функций в компьютерной коэффициентной методике рассмотрим на примере фрагмента методики оценки профессиональной подготовки специалиста, реализующей выставление итоговой балльной оценки «отлично» или «хорошо» на основе G частных балльных оценок, из которых k оценок Х1,…, Хk за практические навыки, а остальные Х(k+1),…, ХG – за теоретические знания.
Логические условия выставления оценок:
· итоговая оценка «отлично» (5) выставляется, если все оценки за практические навыки равны «отлично», а оценки за теоретическую подготовку не ниже «хорошо»;
· итоговая оценка «хорошо» (4) выставляется, если оценка за практические навыки – не «отлично» и все оценки за практические навыки и теоретическую подготовку не ниже «хорошо».
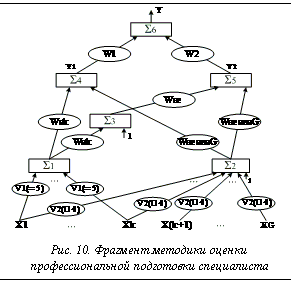
Реализация указанных условий получения итоговой оценки за профессиональную подготовку специалиста иллюстрируется рисунком 10.
Для учета логических условий определения итоговой оценки сначала осуществляется преобразование с использованием изменяемых весовых коэффициентов V1(=5) и V2(<4) значений частных оценок (X1,…, XG) в двоичные величины (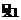 ,…,
,…, ).
).
Затем вычисляются две логические функции с целью проверки условий формирования рассматриваемых оценок.
Проверка первого условия – все оценки за практические навыки равны «отлично» – осуществляется по значению функции конъюнкции 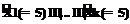 , реализуемой (см. рис. 10) с использованием изменяемых весовых коэффициентов Wиk.
, реализуемой (см. рис. 10) с использованием изменяемых весовых коэффициентов Wиk.
Аналогично проверяется второе условие – все оценки за практические навыки и оценки за теоретическую подготовку должны быть не ниже «хорошо» – по значению функции отрицания дизъюнкции 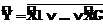 , реализуемой с использованием изменяемого весового коэффициента W не или G.
, реализуемой с использованием изменяемого весового коэффициента W не или G.
Наконец, по вычисленным значениям функций в случае выполнения второго условия формируется итоговая оценка: при выполнении первого условия – «отлично» (5), а при его невыполнении – «хорошо» (4).
При этом осуществляется переход от двоичных переменных к балльным значениям итоговой оценки в соответствии с соотношением Y=W1×Y1+W2×Y2, где Y1 и Y2 – количество двоичных переменных на входах сумматоров Σ4 и Σ5 со значениями, равными 1.
Выбираются следующие значения изменяемых весовых коэффициентов:
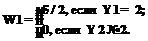

Фрагмент методики, реализующий выставление итоговой оценки «удовлетворительно» или «неудовлетворительно», может быть построен аналогично.
 Для наиболее широкой реализации коэффициентных методик с изменяемыми весовыми коэффициентами целесообразно создание программной оболочки, предназначенной для разработки и реализации методик пользователями, не специализирующимися в области вычислительной техники и программирования.
Для наиболее широкой реализации коэффициентных методик с изменяемыми весовыми коэффициентами целесообразно создание программной оболочки, предназначенной для разработки и реализации методик пользователями, не специализирующимися в области вычислительной техники и программирования.
Созданный с участием авторов вариант программной оболочки получил официальную государственную регистрацию (№ 2008610291 от 14 января 2008 г.) и экспериментально проверен на примере разработки используемой в учебно-воспитательном процессе Ростовского военного института Ракетных войск методики рейтинговой оценки кафедр по итогам обучения за семестр и за учебный год.
В заключение отметим, что компьютерные коэффициентные методики широко используются в практике оценки объектов, относящихся к разнообразным областям деятельности, так как, обладая простотой используемого математического аппарата, обеспечивают рациональное сочетание оперативности получения результата с возможностью количественного его обоснования.
Недостатком существующих коэффициентных методик является невозможность реализации логических функций в процессе получения результата. Логические функции в компьютерных коэффициентных методиках реализуются на основе перехода от традиционно используемых постоянных весовых коэффициентов к изменяемым.
Литература
1. Долгов А.И., Долгов А.И., Журавлев Ю.П. Методика решения некоторых задач оценки объектов с помощью ЦВМ // Автоматика и вычислительная техника. 1965. № 9.
2. Долгов А.И., Мартыненко А.Ф., Преснухин В.В. Коэффициентная методика с изменяемыми весовыми коэффициентами // Искусственный интеллект. Донецк. МОН и ИПИИ «Наука i освiта». 2008. Т. 4.



 Основным достоинством компьютерной методики оценки объектов с изменяемыми весовыми коэффициентами является возможность учета произвольных логических условий получения промежуточных и выходных показателей на основе реализации логических функций над характеризующими обрабатываемые входные и промежуточные показатели двоичными величинами.
Основным достоинством компьютерной методики оценки объектов с изменяемыми весовыми коэффициентами является возможность учета произвольных логических условий получения промежуточных и выходных показателей на основе реализации логических функций над характеризующими обрабатываемые входные и промежуточные показатели двоичными величинами. , характеризующими соотношение между значением показателя Хi и некоторой выбираемой величиной (a). Здесь Ä – один из знаков: =, >, <, ¹, £, ³. Возможные варианты проверяемых альтернативных условий приведеы в таблице.
, характеризующими соотношение между значением показателя Хi и некоторой выбираемой величиной (a). Здесь Ä – один из знаков: =, >, <, ¹, £, ³. Возможные варианты проверяемых альтернативных условий приведеы в таблице.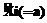

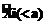
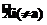


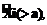 см. табл.) с использованием изменяемого весового коэффициента V(>a) значения обрабатываемого показателя Хi в двоичную величину
см. табл.) с использованием изменяемого весового коэффициента V(>a) значения обрабатываемого показателя Хi в двоичную величину 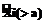 .
.
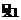 ,…,
,…, ).
).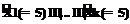 , реализуемой (см. рис. 10) с использованием изменяемых весовых коэффициентов Wиk.
, реализуемой (см. рис. 10) с использованием изменяемых весовых коэффициентов Wиk.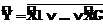 , реализуемой с использованием изменяемого весового коэффициента W не или G.
, реализуемой с использованием изменяемого весового коэффициента W не или G.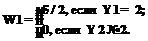

 Для наиболее широкой реализации коэффициентных методик с изменяемыми весовыми коэффициентами целесообразно создание программной оболочки, предназначенной для разработки и реализации методик пользователями, не специализирующимися в области вычислительной техники и программирования.
Для наиболее широкой реализации коэффициентных методик с изменяемыми весовыми коэффициентами целесообразно создание программной оболочки, предназначенной для разработки и реализации методик пользователями, не специализирующимися в области вычислительной техники и программирования.