В последние годы теория сложных сетей широко используется в физических, биологических, технических и общественных науках как один из унифицирующих подходов, позволяющих описывать системы в виде комплекса взаимодействующих элементов, формирующих организованное целое [1]. Сложные сети, естественные и искусственные, имеют нетривиальную топологию, которая изучается на основе анализа ряда характеристик, таких как распределение степеней, кластеризация, кратчайшие пути и т.д. [2]. Изучение свойств сетей реального мира (метаболические сети, Интернет, WWW, сети цитирования, сети сотрудничества и другие) позволяет глубже понять сформировавшие их механизмы, которые обусловливают особенности структуры; их связь с принципами формирования сетей не всегда очевидна и является предметом многочисленных обсуждений.
Эмпирические исследования показали, что, хотя локальные взаимодействия между индивидуальными компонентами чрезвычайно разнообразны, в целом многие сложные сети имеют общие топологические свойства, такие как масштабная инвариантность, мало-мировое свойство или кластеризация [1]. Для объяснения феномена масштабной инвариантности, свойственной большому числу сетей реального мира, А.-Л. Барабаси и Р. Альберт предложили рассмотреть модели растущих сетей. Они показали, что только в случае, если вероятность соединения поступающей в сеть вершины с вершиной i пропорциональна ее степени ki, порождаемая сеть будет иметь распределение степеней в виде p(k)~k-g с g=3.
В целом модель Барабаси объясняет основные особенности большей части сетей реального мира, но имеет существенный недостаток – строго фиксированное значение показателя степенного распределения g=3, в то время как эмпирические исследования показали, что для сетей реального мира показатель g варьируется от 1 до 3.
Для устранения этого недостатка была введена обобщенная модель Альберт–Барабаси, в которой процесс роста сети сопровождается добавлением новых ребер и пересвязыванием существующих. В результате показатель распределения перестает быть фиксированным, g<3. В [3] показано, что в этом случае распределение степеней сети описывается распределением Цаллиса в виде
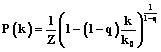 ,
,
где 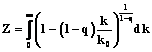 .
.
При q®1 это распределение сводится к экспоненциальному, тогда как при q>1 и больших k имеет вид степенного распределения. Здесь q – параметр неэкстенсивности, являющийся мерой сложности системы. Эмпирические исследования растущих сетей показали, что различные процессы формирования сети могут приводить к структурам, топологические свойства которых описываются распределением [4].
Для сетей реального мира наряду с основными механизмами характерны дополнительные, затрагивающие и собственно процесс роста, и принцип предпочтительного присоединения. К таким ме- ханизмам, имеющим место во многих сетях реального мира, относятся нарушение принципа линейности предпочтительного присоединения и конкуренция узлов. Кроме того, рост сетей реального мира нередко сопровождается старением и удалением узлов. И самое главное, эти механизмы в сетях реального мира действуют комбинированно.
Аналитические методы исследования растущих сетей базируются на трех подходах [1]. В первом случае предполагается, что известна временная эволюция среднего значения степени i-го узла ki(t); распределение степеней сети p(k, t) получается из гипотезы регулярного добавления узлов, что приводит к однородному распределению времен рождений узлов {ti}, и определения  [1]. Второй метод основан на подходе основного уравнения; вводится вероятность p(k, ti, t) того, что в момент t узел i, рожденный в момент ti, имеет степень k [5]. В рамках третьего подхода, называемого «rate – equation approach», исследуется скорость изменения nk(t) – среднего числа узлов в сети, имеющих степень k в момент t [2]. Необходимо подчеркнуть, что все три подхода описывают непрерывно растущие сети.
[1]. Второй метод основан на подходе основного уравнения; вводится вероятность p(k, ti, t) того, что в момент t узел i, рожденный в момент ti, имеет степень k [5]. В рамках третьего подхода, называемого «rate – equation approach», исследуется скорость изменения nk(t) – среднего числа узлов в сети, имеющих степень k в момент t [2]. Необходимо подчеркнуть, что все три подхода описывают непрерывно растущие сети.
Аналитические исследования позволили получить интересные результаты. В рамках первого подхода проведен анализ топологии сетей с конкурирующими узлами при различных распределениях скрытых переменных [1]. В частности, показано, что рост степеней узлов является функцией скрытых переменных. Топология такой сети зависит от конкретного вида распределения значений скрытых переменных. Например, в случае однородного распределения топология сети с конкурирующими узлами определяется выражением  , где c*=1,255.
, где c*=1,255.
В рамках подхода основного уравнения показано, что растущие с нелинейным предпочтительным присоединением 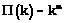 сети характеризуются распределением степеней в виде P(k)=
сети характеризуются распределением степеней в виде P(k)= 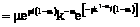 , где параметр m определяется из решения уравнения
, где параметр m определяется из решения уравнения 
 [5].
[5].
В последнее время интенсивное изучение биологических сетей индуцировало изучение растущих сетей с удалением вершин. Очевидно, этот механизм присущ многим сетям реального мира. Например, классические сложные сети Интернет и WWW благодаря добавлению компьютеров и новых документов растут, но в обоих случаях происходит удаление узлов (ломаются компьютеры и удаляются документы). Следовательно, актуальным является изучение влияния удаления вершин на топологию сложных сетей, на их устойчивость, а также на динамические процессы в сетях.
Топология растущих сетей с линейным предпочтительным присоединением П(k)~ak+b и удалением вершин исследована в рамках третьего подхода [2]. Показано, что распределение степеней такой сети имеет вид

и при b=0 топология сети сводится к экспоненциальной [2]. Параметр b является функцией вероятности удаления вершин, их исходной привлекательности, числа добавленных ребер и средней степени вершин.
Необходимо отметить, что, хотя многие свойства систем реального мира были исследованы аналитически, в целом в рамках аналитических подходов учет комбинированных механизмов весьма затруднителен.
В данной работе приводится обобщенный алгоритм численного моделирования растущих сетей с нелинейным предпочтительным присоединением, конкуренцией и удалением узлов. Результаты численного анализа показывают, что топология таких сетей достаточно точно описывается распределением Цаллиса. Полученные результаты применяются к описанию реальной компьютерной сети из ~7×103 узлов [3]. Показано, что сеть дисассортативна и имеет достаточно малый коэффициент кластеризации.
Алгоритм генерации сети. Рассмотрим обобщение принципа предпочтительного присоединения – нелинейное предпочтительное присоединение с конкуренцией узлов. В случае нелинейного предпочтительного присоединения вероятность присоединения новой вершины к i-й вершине, уже находящейся в сети, равна  , где 0£v£1. Отметим, что при v=0 присоединение будет однородным и полученная сеть имеет экспоненциальную топологию
, где 0£v£1. Отметим, что при v=0 присоединение будет однородным и полученная сеть имеет экспоненциальную топологию 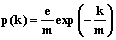 , где m – количество ребер, с которыми добавляется в сеть новая вершина. Случай v=1 соответствует линейному предпочтительному присоединению и приводит к масштабно-инвариантной сети с показателем g=3.
, где m – количество ребер, с которыми добавляется в сеть новая вершина. Случай v=1 соответствует линейному предпочтительному присоединению и приводит к масштабно-инвариантной сети с показателем g=3.
В реальных сетях нередко «предпочтительность присоединения» бывает связана не только с количеством имеющихся связей, но и с дополнительными факторами, для учета которых вводится скрытая переменная. Введение ее позволяет узлам конкурировать за приобретение связей. В отличие от сети Барабаси в сети с конкуренцией узлов более молодые вершины могут приобретать больше связей, чем старые.
Сгенерируем сети с комбинированным механизмом роста, то есть присоединим поступающие узлы в соответствии с принципом нелинейного предпочтительного присоединения. Одновременно введем механизм конкуренции узлов. Допускается также возможность удаления узлов.
Временная эволюция сети осуществляется по следующему алгоритму:
1) в начальный момент в сети имеется m0 изолированных вершин;
2) в каждый дискретный момент происходит одно из трех событий:
 – с вероятностью q в сеть добавляется новая вершина, которой приписывается случайное значение скрытой переменной h, равномерно распределенное на интервале [0, 1]; новая вершина связывается ребром с одной из вершин в сети в соответствии с принципом нелинейного предпочтительного присоединения и с учетом скрытых переменных hi: П(ki)=(kihi)n/Sj(kjhj)n;
– с вероятностью q в сеть добавляется новая вершина, которой приписывается случайное значение скрытой переменной h, равномерно распределенное на интервале [0, 1]; новая вершина связывается ребром с одной из вершин в сети в соответствии с принципом нелинейного предпочтительного присоединения и с учетом скрытых переменных hi: П(ki)=(kihi)n/Sj(kjhj)n;
– с вероятностью p в сеть добавляется n ребер; один конец каждого ребра выбирается случайно, а второй – в соответствии с принципом нелинейного предпочтительного присоединения с учетом скрытых переменных вершин;
– с вероятностью 1-p-q из сети удаляется одна случайно выбранная вершина; при этом удаляются все инцидентные ей ребра.
Особенности топологии. Результаты моделирования показывают, что при изменении параметра нелинейности 0£v£1 происходит фазовый переход от экспоненциальной сети (v=0) к степенной (v=1) (рис. 1), что согласуется с аналитическими результатами. Необходимо подчеркнуть, что экспоненциальная сеть (v=0) ассортативна, тогда как сеть со степенным распределением степеней (v=1) является некоррелированной. Механизм нелинейного предпочтительного присоединения (0<1) приводит к нарушению структуры масштабно-инвариантной сети, а именно, сокращается прямолинейный участок в распределении степеней вершин. Кроме того, появляется характерный изгиб кривой, и структура сети становится относительно однородной. В результате уменьшается значение максимальной степени узлов сети.
Значения параметров p, q и r=1-p-q следующим образом влияют на топологию сетей. Если зафиксировать значение вероятности добавления ребер p, то с уменьшением вероятности добавления новой вершины q и, как следствие, с ростом вероятности удаления вершины r происходят трансформации топологии сети. Если зафиксировать параметр q, то с уменьшением p увеличивается изгиб кривой распределения степеней (рис. 2). Аналогичным образом влияет и уменьшение числа добавляемых за итерацию ребер n при прочих фиксированных параметрах.
Результаты анализа данных. В рамках приведенной выше модели описана компьютерная сеть из ~7×103 узлов, являющаяся подсетью Интернета [3]. Распределение степеней для данной сети показано на рисунке 3. Средняя степень вершин сети 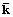 =14. Эта сеть растет как вследствие присоединения к ней новых узлов, так и за счет появления новых связей. Очевидно, что происходит и процесс удаления узлов из сети.
=14. Эта сеть растет как вследствие присоединения к ней новых узлов, так и за счет появления новых связей. Очевидно, что происходит и процесс удаления узлов из сети.
Для описания данной сети использовался приведенный выше алгоритм. Из подгонки были определены значения параметров модели: v=0,97, N=50 000, m0=20, p=0,88, n=1, q=0,1. В качестве критерия оптимальности подгонки использовался минимум суммы квадратов отклонений теоретических и экспериментальных значений. Ограничениями выступали значение средней степени и общее число узлов в сети.
С использованием распределения Цаллиса проведена подгонка распределений степеней для эмпирической и сгенерированной сетей. Результаты показаны на рисунке 4А и В соответственно. Значения параметра неэкстенсивности q=1,1 и q=1,08 соответственно.
Следовательно, для растущих сетей с нелинейным предпочтительным присоединением, конкуренцией и удалением узлов характерно распределение степеней в форме распределения Цаллиса.
Кроме того, сравнивались экспериментальная и сгенерированная сети по таким характеристикам, как двух- и трехвершинные корреляции и вершинная промежуточная значимость.
Двухвершинные корреляции степеней вершин характеризуются условной вероятностью  того, что вершины степеней k и k¢ связаны. Для практических целей анализируют среднюю степень ближайших соседей как функцию степени вершины, определяемую следующим образом:
того, что вершины степеней k и k¢ связаны. Для практических целей анализируют среднюю степень ближайших соседей как функцию степени вершины, определяемую следующим образом: 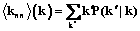 [2]. Для некоррелированных сетей áknnñ(k) не зависит от k. Если áknnñ(k) с ростом k возрастает, то есть оказывается, что вершины большей степени предпочтительно соединены с вершинами большей степени, то корреляции степеней вершин в сети носят ассортативный характер. Если с ростом k значения áknnñ(k) уменьшаются, то есть вершины большей степени преимущественно соединены с вершинами малых степеней, характер корреляций дисассортативный.
[2]. Для некоррелированных сетей áknnñ(k) не зависит от k. Если áknnñ(k) с ростом k возрастает, то есть оказывается, что вершины большей степени предпочтительно соединены с вершинами большей степени, то корреляции степеней вершин в сети носят ассортативный характер. Если с ростом k значения áknnñ(k) уменьшаются, то есть вершины большей степени преимущественно соединены с вершинами малых степеней, характер корреляций дисассортативный.
Зависимость áknnñ(k) для сгенерированной сети представлена на рисунке 5. Как и для экспериментальной сети [3], с ростом k значения áknnñ уменьшаются. Это указывает на дисассортативный характер сети, присущий и Интернету в целом. В данном случае по результатам подгонки knn(k)=ak -s, где s=0,29.
Информацию о трехвершинных корреляциях можно получить из коэффициента кластеризации, определяемого как вероятность того, что две вершины, смежные с данной, также связаны ребром [2]. Численно локальный коэффициент кластеризации ci для i-й вершины может быть вычислен как отношение числа ei ребер между ki соседями вершины i к его максимально возможному значению  , то есть
, то есть  . Зависимость среднего коэффициента кластеризации от степени áсñ(k) вычисляется путем усреднения коэффициентов кластеризации для вершин, имеющих одинаковую степень k. Коэффициент кластеризации сети вычисляется как среднее значение коэффициентов кластеризации всех вершин сети.
. Зависимость среднего коэффициента кластеризации от степени áсñ(k) вычисляется путем усреднения коэффициентов кластеризации для вершин, имеющих одинаковую степень k. Коэффициент кластеризации сети вычисляется как среднее значение коэффициентов кластеризации всех вершин сети.
Значение коэффициента кластеризации для сгенерированной сети составило C»0,06. С увеличением степени среднее значение коэффициента кластеризации уменьшается, по результатам подгонки данная зависимость имеет степенной характер c(k)=ek -Y, где Y=0,44.
Важной локальной характеристикой является промежуточная значимость узлов сети b [2]. Промежуточная значимость  узла i для вершин j и l (j¹l) определяется как доля кратчайших путей между этими вершинами, проходящих через вершину i. Общая промежуточная значимость вершины i определяется как
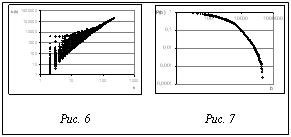
узла i для вершин j и l (j¹l) определяется как доля кратчайших путей между этими вершинами, проходящих через вершину i. Общая промежуточная значимость вершины i определяется как  . Значения этой величины вычислены для анализируемой сети. На рисунке 6 показана зависимость промежуточной значимости от степени вершин, а на рисунке 7 – кумулятивное распределение P(b), то есть вероятность того, что вершина имеет промежуточное значение, большее b. Знание распределения P(b) необходимо для изучения и управления трафиком.
. Значения этой величины вычислены для анализируемой сети. На рисунке 6 показана зависимость промежуточной значимости от степени вершин, а на рисунке 7 – кумулятивное распределение P(b), то есть вероятность того, что вершина имеет промежуточное значение, большее b. Знание распределения P(b) необходимо для изучения и управления трафиком.
 Анализ компьютерной сети, которая является подсетью Интернета, показывает, что полученные в результате подгонки значения Y=0,44 и s=0,29 не совпадают с показателями, найденными для глобального Интернета на уровне автономных систем и маршрутизаторов Y=0,75±0,03 и s=0,5±0,1 [2]. Это, по-видимому, связано с конкуренцией узлов в сети, что приводит к мультискейлинговому поведению растущей сети.
Анализ компьютерной сети, которая является подсетью Интернета, показывает, что полученные в результате подгонки значения Y=0,44 и s=0,29 не совпадают с показателями, найденными для глобального Интернета на уровне автономных систем и маршрутизаторов Y=0,75±0,03 и s=0,5±0,1 [2]. Это, по-видимому, связано с конкуренцией узлов в сети, что приводит к мультискейлинговому поведению растущей сети.
 Распространение вирусов и стратегия лечения. В компьютерных системах без автомати- ческого обновления антивирусных программ распространение вирусов в сетях с заданной топологией описывается моделью SIS, которая предполагает, что узлы в сети могут находиться в одном из двух состояний: восприимчивом (S) и инфицированном (I) [2]. В этой модели восприимчивые узлы инфицируются, переходят в инфицированное состояние и снова становятся восприимчивыми спустя какое-то время, по истечении которого будут здоровыми. Затем они вновь могут подвергнуться инфицированию. Таким образом, процесс распространения вирусов описывается реакцией
Распространение вирусов и стратегия лечения. В компьютерных системах без автомати- ческого обновления антивирусных программ распространение вирусов в сетях с заданной топологией описывается моделью SIS, которая предполагает, что узлы в сети могут находиться в одном из двух состояний: восприимчивом (S) и инфицированном (I) [2]. В этой модели восприимчивые узлы инфицируются, переходят в инфицированное состояние и снова становятся восприимчивыми спустя какое-то время, по истечении которого будут здоровыми. Затем они вновь могут подвергнуться инфицированию. Таким образом, процесс распространения вирусов описывается реакцией  где l и m – вероятности соответствующих переходов. Для конкретной сети процесс распространения определяется ее топологией и вероятностью l перехода узла из состояния S в состояние I (здоровый узел в сети при контакте с зараженным узлом становится инфицированным). Можно показать, что существует пороговое значение вероятности перехода lc, такое, что при значениях llc доля инфицированных узлов r будет больше нуля, то есть вирусы в сети распространяются неограниченно долго.
где l и m – вероятности соответствующих переходов. Для конкретной сети процесс распространения определяется ее топологией и вероятностью l перехода узла из состояния S в состояние I (здоровый узел в сети при контакте с зараженным узлом становится инфицированным). Можно показать, что существует пороговое значение вероятности перехода lc, такое, что при значениях llc доля инфицированных узлов r будет больше нуля, то есть вирусы в сети распространяются неограниченно долго.
Обращение в нуль эпидемического порога распространения вируса в масштабно-инвариантных сетях коренится в бесконечной дисперсии распределения степеней. Действительно, порог lc зависит от дисперсии [2]:  .
.
Для случайных сетей распределение степеней является пуассоновским. Как результат, дисперсия конечна и, следовательно, порог lc конечен. Напротив, если вирусы распространяются в масштабно-инвариантной сети, для которой P(k) следует степенному закону с g=3, значение является бесконечным и эпидемический порог lc=0. Поэтому, чтобы восстановить конечный эпидемический порог, ниже которого инфекция затухает, необходимо индуцировать конечную дисперсию. Отметим, что, если масштабно-инвариантная сеть имеет конечный размер, эпидемический порог конечен [2] и имеет значение
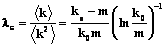 .
.
Поскольку причиной возникновения бесконечной является «хвост» распределения степеней, где доминируют хабы, ожидается, что лечение всех хабов со степенью, большей некоторой степени k0, изменит топологию сети, восстановит конечность и эпидемический порог станет отличным от нуля. Это выражение показывает, что, чем больше хабов вылечивается (то есть чем меньше k0), тем больше отклонение от степенного распределения и значение эпидемического порога. Поэтому наиболее эффективная стратегия против эпидемий – вылечить так много хабов, как это возможно с экономической точки зрения.
Стратегия уничтожения вирусов, базирующаяся на последовательном лечении узлов с самой высокой степенью (хабы), приводит к изменению топологии сети и увеличению lc.
На основании изложенного сделаем следующие выводы. Топология растущих сетей с нелинейным предпочтительным присоединением, конкуренцией и удалением узлов достаточно точно описывается распределением Цаллиса.
Характер корреляций в сети является функцией показателя нелинейного предпочтительного присоединения и с его изменением меняется от случайного к ассортативному.
Включение механизма конкуренции узлов может изменить характер корреляций от ассортативного к дисассортативному.
Рассмотренная стратегия лечения сети, основанная на последовательном лечении и иммунизации 2,2 % узлов наибольшей степени, позволяет остановить распространение эпидемии.
Разработанное программное обеспечение может использоваться для решения задач оптимального управления трафиком, выбора эффективной стратегии лечения вирусов в реальных сетях и изучения контактных явлений в сетях.
Литература
1. Albert R., Barabasi A.-L. Statistical Mechanics of Complex Networks // Rev. Mod. Phys. 2002. Vol. 74, pp. 43–97.
2. Vazquez A., Pastor-Satorras R., Vespignani A. Large-scale topological and dynamical properties of the Internet // Phys Rev E. 2002. Vol. 65.
3. Гаджиев Б.Р., Калинкина Е.А., Крюков Ю.А., Прогулова Т.Б. Контактные явления в сетях со статистикой q-типа // Математика. Компьютер. Образование: cб. тр. XV Междунар. конф.; под общ. ред. Г.Ю. Ризниченко. Ижевск: НИЦ «Регулярная и хаотическая динамика», 2008. Т. 2. С. 121–130.
4. Tsallis C. Nonextensive statistics: theoretical, experimental and computational evidences and connections // Braz. J. Phys. 1999. Vol. 29, pp. 1–35.
5. Dorogovtsev S.N., Mendes J.F.F. Scaling properties of scale-free evolving networks: Continuous approach // Phys. Rev. E. 2001. Vol. 63.



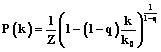 ,
,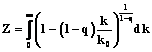 .
. [1]. Второй метод основан на подходе основного уравнения; вводится вероятность p(k, ti, t) того, что в момент t узел i, рожденный в момент ti, имеет степень k [5]. В рамках третьего подхода, называемого «rate – equation approach», исследуется скорость изменения nk(t) – среднего числа узлов в сети, имеющих степень k в момент t [2]. Необходимо подчеркнуть, что все три подхода описывают непрерывно растущие сети.
[1]. Второй метод основан на подходе основного уравнения; вводится вероятность p(k, ti, t) того, что в момент t узел i, рожденный в момент ti, имеет степень k [5]. В рамках третьего подхода, называемого «rate – equation approach», исследуется скорость изменения nk(t) – среднего числа узлов в сети, имеющих степень k в момент t [2]. Необходимо подчеркнуть, что все три подхода описывают непрерывно растущие сети. , где c*=1,255.
, где c*=1,255.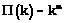 сети характеризуются распределением степеней в виде P(k)=
сети характеризуются распределением степеней в виде P(k)= 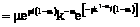 , где параметр m определяется из решения уравнения
, где параметр m определяется из решения уравнения 
 [5].
[5].
 , где 0£v£1. Отметим, что при v=0 присоединение будет однородным и полученная сеть имеет экспоненциальную топологию
, где 0£v£1. Отметим, что при v=0 присоединение будет однородным и полученная сеть имеет экспоненциальную топологию 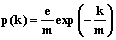 , где m – количество ребер, с которыми добавляется в сеть новая вершина. Случай v=1 соответствует линейному предпочтительному присоединению и приводит к масштабно-инвариантной сети с показателем g=3.
, где m – количество ребер, с которыми добавляется в сеть новая вершина. Случай v=1 соответствует линейному предпочтительному присоединению и приводит к масштабно-инвариантной сети с показателем g=3.
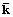 =14. Эта сеть растет как вследствие присоединения к ней новых узлов, так и за счет появления новых связей. Очевидно, что происходит и процесс удаления узлов из сети.
=14. Эта сеть растет как вследствие присоединения к ней новых узлов, так и за счет появления новых связей. Очевидно, что происходит и процесс удаления узлов из сети. того, что вершины степеней k и k¢ связаны. Для практических целей анализируют среднюю степень ближайших соседей как функцию степени вершины, определяемую следующим образом:
того, что вершины степеней k и k¢ связаны. Для практических целей анализируют среднюю степень ближайших соседей как функцию степени вершины, определяемую следующим образом: 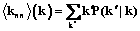 [2]. Для некоррелированных сетей áknnñ(k) не зависит от k. Если áknnñ(k) с ростом k возрастает, то есть оказывается, что вершины большей степени предпочтительно соединены с вершинами большей степени, то корреляции степеней вершин в сети носят ассортативный характер. Если с ростом k значения áknnñ(k) уменьшаются, то есть вершины большей степени преимущественно соединены с вершинами малых степеней, характер корреляций дисассортативный.
[2]. Для некоррелированных сетей áknnñ(k) не зависит от k. Если áknnñ(k) с ростом k возрастает, то есть оказывается, что вершины большей степени предпочтительно соединены с вершинами большей степени, то корреляции степеней вершин в сети носят ассортативный характер. Если с ростом k значения áknnñ(k) уменьшаются, то есть вершины большей степени преимущественно соединены с вершинами малых степеней, характер корреляций дисассортативный. , то есть
, то есть  . Зависимость среднего коэффициента кластеризации от степени áсñ(k) вычисляется путем усреднения коэффициентов кластеризации для вершин, имеющих одинаковую степень k. Коэффициент кластеризации сети вычисляется как среднее значение коэффициентов кластеризации всех вершин сети.
. Зависимость среднего коэффициента кластеризации от степени áсñ(k) вычисляется путем усреднения коэффициентов кластеризации для вершин, имеющих одинаковую степень k. Коэффициент кластеризации сети вычисляется как среднее значение коэффициентов кластеризации всех вершин сети. узла i для вершин j и l (j¹l) определяется как доля кратчайших путей между этими вершинами, проходящих через вершину i. Общая промежуточная значимость вершины i определяется как
узла i для вершин j и l (j¹l) определяется как доля кратчайших путей между этими вершинами, проходящих через вершину i. Общая промежуточная значимость вершины i определяется как  . Значения этой величины вычислены для анализируемой сети. На рисунке 6 показана зависимость промежуточной значимости от степени вершин, а на рисунке 7 – кумулятивное распределение P(b), то есть вероятность того, что вершина имеет промежуточное значение, большее b. Знание распределения P(b) необходимо для изучения и управления трафиком.
. Значения этой величины вычислены для анализируемой сети. На рисунке 6 показана зависимость промежуточной значимости от степени вершин, а на рисунке 7 – кумулятивное распределение P(b), то есть вероятность того, что вершина имеет промежуточное значение, большее b. Знание распределения P(b) необходимо для изучения и управления трафиком.
 Распространение вирусов и стратегия лечения. В компьютерных системах без автомати- ческого обновления антивирусных программ распространение вирусов в сетях с заданной топологией описывается моделью SIS, которая предполагает, что узлы в сети могут находиться в одном из двух состояний: восприимчивом (S) и инфицированном (I) [2]. В этой модели восприимчивые узлы инфицируются, переходят в инфицированное состояние и снова становятся восприимчивыми спустя какое-то время, по истечении которого будут здоровыми. Затем они вновь могут подвергнуться инфицированию. Таким образом, процесс распространения вирусов описывается реакцией
Распространение вирусов и стратегия лечения. В компьютерных системах без автомати- ческого обновления антивирусных программ распространение вирусов в сетях с заданной топологией описывается моделью SIS, которая предполагает, что узлы в сети могут находиться в одном из двух состояний: восприимчивом (S) и инфицированном (I) [2]. В этой модели восприимчивые узлы инфицируются, переходят в инфицированное состояние и снова становятся восприимчивыми спустя какое-то время, по истечении которого будут здоровыми. Затем они вновь могут подвергнуться инфицированию. Таким образом, процесс распространения вирусов описывается реакцией  где l и m – вероятности соответствующих переходов. Для конкретной сети процесс распространения определяется ее топологией и вероятностью l перехода узла из состояния S в состояние I (здоровый узел в сети при контакте с зараженным узлом становится инфицированным). Можно показать, что существует пороговое значение вероятности перехода lc, такое, что при значениях llc доля инфицированных узлов r будет больше нуля, то есть вирусы в сети распространяются неограниченно долго.
где l и m – вероятности соответствующих переходов. Для конкретной сети процесс распространения определяется ее топологией и вероятностью l перехода узла из состояния S в состояние I (здоровый узел в сети при контакте с зараженным узлом становится инфицированным). Можно показать, что существует пороговое значение вероятности перехода lc, такое, что при значениях llc доля инфицированных узлов r будет больше нуля, то есть вирусы в сети распространяются неограниченно долго. .
.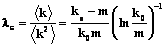 .
.