При подготовке космонавтов активно используются тренажерные комплексы. Одной из важных задач при разработке многих комплексов является моделирование вида земной поверхности, наблюдаемого космонавтом из космического аппарата (КА), летящего по околоземной орбите. В тренажерном комплексе это достигается с помощью подсистемы моделирования и подсистемы визуализации. В подсистему визуализации предварительно загружается виртуальная сцена, которая содержит трехмерные модели КА и Земли, а также виртуальную камеру, связанную с КА. Подсистема моделирования периодически (например, каждые 40 мс) рассчитывает в некоторой системе координат положение и ориентацию динамических объектов и передает их по информационному протоколу в подсистему визуализации. В подсистеме визуализации по полученным данным производится установка трехмерных моделей в виртуальной сцене, а затем вся сцена отображается на дисплей средства наблюдения космонавта [1].
В качестве базовой системы координат для расчета параметров движения динамических объектов можно выбрать геоцентрическую систему, однако часто в системах визуализации выбирают систему координат, жестко связанную с КА. В этом случае КА считается неподвижным, а движение Земли моделируется относительно КА. При этом модель Земли располагается и ориентируется таким образом, чтобы наблюдаемая из КА область земной поверхности совпадала с областью, которую видел бы наблюдатель, если бы начало базовой системы координат располагалось в центре Земли, а КА двигался по орбите вокруг нее. Данная статья посвящена вычислениям положения и ориентации (задаваемой углами Эйлера–Крылова) модели Земли в системе координат, жестко связанной с КА, исходя из заданных параметров околоземной орбиты КА.
Моделирование движения КА по орбите
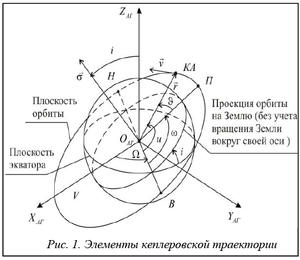 На околоземном внеатмосферном участке полета КА его центр масс двигается в основном под действием силы притяжения Земли (при условии, что двигатели КА выключены). Если принять, что Земля сферическая и неподвижная, а масса КА пренебрежимо мала по отношению к массе Земли, то движение центра масс КА в гравитационном поле Земли можно смоделировать кеплеровским движением, то есть по кеплеровской траекто- рии [2]. В данной статье рассматривается движение КА по эллиптической траектории (орбите), один из фокусов которой совпадает с центром Земли (рис. 1).
На околоземном внеатмосферном участке полета КА его центр масс двигается в основном под действием силы притяжения Земли (при условии, что двигатели КА выключены). Если принять, что Земля сферическая и неподвижная, а масса КА пренебрежимо мала по отношению к массе Земли, то движение центра масс КА в гравитационном поле Земли можно смоделировать кеплеровским движением, то есть по кеплеровской траекто- рии [2]. В данной статье рассматривается движение КА по эллиптической траектории (орбите), один из фокусов которой совпадает с центром Земли (рис. 1).
Чтобы полностью определить кеплеровское движение КА, то есть положение и скорость КА в любой момент, в теорию полета вводится набор из 6 независимых параметров, называемых элементами кеплеровской траектории. Это долгота восходящего узла W, наклонение плоскости орбиты к плоскости экватора i, аргумент перигея w, эксцентриситет e, фокальный параметр p, а также время прохождения КА через перигей П орбиты tp. При невозмущенном кеплеровском движении эти параметры остаются постоянными на протяжении всего времени полета КА.
Для определения параметров кеплеровской траектории движения КА в трехмерном пространстве используется абсолютная геоцентрическая система координат EАГ (рис. 1). Начало системы координат OАГ расположено в центре Земли. Ось OАГZАГ совпадает с осью вращения Земли и направлена на Северный полюс. Ось OАГXАГ перпендикулярна ей и направлена в точку весеннего равноденствия V. Ось OАГYАГ дополняет систему координат до правосторонней.
 Положение КА в плоскости эллиптической орбиты в момент t задается углом J (истинная аномалия) и длиной r радиус-вектора
Положение КА в плоскости эллиптической орбиты в момент t задается углом J (истинная аномалия) и длиной r радиус-вектора  , направленного из центра Земли в центр масс КА. Вычисление J и r в момент t по заданным параметрам орбиты приводится в [2–4].
, направленного из центра Земли в центр масс КА. Вычисление J и r в момент t по заданным параметрам орбиты приводится в [2–4].
Движение КА как твердого тела можно смоделировать, определив в каждый момент его положение и ориентацию в системе координат EАГ. В теории полета положение центра масс КА в системе EАГ определяется с помощью сопровождающей системы координат EС. Начало координат OС совпадает с OАГ. Ось OСXC совпадает по направлению с текущим радиус-вектором  , ось OСZC – с векторной константой площадей
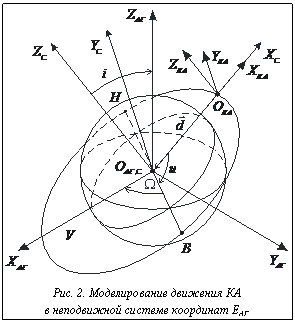
, ось OСZC – с векторной константой площадей 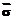 (рис. 1), а ось OСYC дополняет эти оси до правосторонней системы координат (рис. 2). В этой системе координат центр масс КА всегда имеет координаты (r, 0, 0, 1). Введем дополнительную систему координат EКА, жестко связанную с КА, то есть при движении КА координаты его точек в системе EКА не меняются. Начало координат OКА расположим в центре масс КА, а оси координат направим так же, как в системе EС. Тогда положение и ориентацию КА в системе EАГ можно определить, вычислив матрицу преобразования координат точек КА из системы EКА в систему EАГ.
(рис. 1), а ось OСYC дополняет эти оси до правосторонней системы координат (рис. 2). В этой системе координат центр масс КА всегда имеет координаты (r, 0, 0, 1). Введем дополнительную систему координат EКА, жестко связанную с КА, то есть при движении КА координаты его точек в системе EКА не меняются. Начало координат OКА расположим в центре масс КА, а оси координат направим так же, как в системе EС. Тогда положение и ориентацию КА в системе EАГ можно определить, вычислив матрицу преобразования координат точек КА из системы EКА в систему EАГ.
Из линейной алгебры известно: если в аффинном пространстве имеются системы координат  и
и 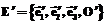 , где
, где  и
и 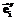 – ортонормированные векторы базисов, а O и O¢ – начала соответствующих систем координат и E переводится в E¢ с помощью произвольной последовательности поворотов и переносов, последовательно совмещаясь с промежуточными системами координат E1,…, Ek-1, то имеют место следующие соотношения:
– ортонормированные векторы базисов, а O и O¢ – начала соответствующих систем координат и E переводится в E¢ с помощью произвольной последовательности поворотов и переносов, последовательно совмещаясь с промежуточными системами координат E1,…, Ek-1, то имеют место следующие соотношения:
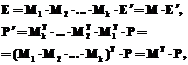 (1)
(1)
где P – координаты точки P в системе E; P¢ – координаты точки P в системе E¢; Mi – матрица, переводящая систему Ei-1 в систему Ei либо путем поворота Ei-1 вокруг оси 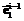 на угол a (
на угол a (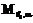 ), или вокруг
), или вокруг 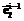 на угол b (
на угол b ( ), или вокруг оси
), или вокруг оси 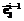 на угол g (
на угол g ( ) (положительным считается поворот системы координат по часовой стрелке, если смотреть с конца вектора, вокруг которого осуществляется поворот), либо путем переноса Ei на вектор
) (положительным считается поворот системы координат по часовой стрелке, если смотреть с конца вектора, вокруг которого осуществляется поворот), либо путем переноса Ei на вектор  (
( ). Матрицы
). Матрицы 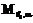 ,
,  ,
,  и
и  имеют вид
имеют вид
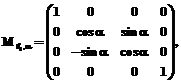



Матрицы  ,
,  ,
,  и
и  обозначаются в данной статье как
обозначаются в данной статье как 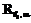 ,
, 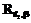 ,
, 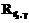 и
и  соответственно.
соответственно.
Таким образом, преобразование PКА в PАГ можно получить, если мысленно совместить систему EКА с системой EС, а затем с системой EАГ с помощью последовательного переноса и поворотов системы EКА (рис. 2):
· перенос на вектор 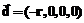 вдоль оси OXКА;
вдоль оси OXКА;
· поворот на угол u вокруг оси OZC, где u – аргумент широты, u = w + J;
· поворот на угол i вокруг оси 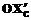 , полученной после первого поворота EС;
, полученной после первого поворота EС;
· поворот на угол W вокруг оси 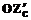 , полученной после второго поворота EС.
, полученной после второго поворота EС.
По формуле (1) результирующий перевод системы EКА в систему EАГ имеет следующий матричный вид: 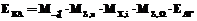 , а преобразование координат PКА в PАГ вид
, а преобразование координат PКА в PАГ вид
 . (2)
. (2)
Имитация движения КА по орбите в подсистеме визуализации
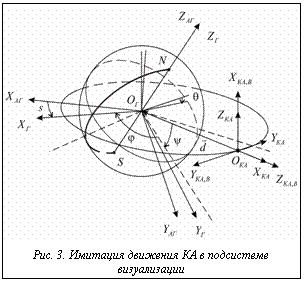 Как отмечалось ранее, движение КА в подсистеме визуализации имитируется путем переноса и ориентации в виртуальной сцене модели Земли относительно неподвижной модели КА (рис. 3).
Как отмечалось ранее, движение КА в подсистеме визуализации имитируется путем переноса и ориентации в виртуальной сцене модели Земли относительно неподвижной модели КА (рис. 3).
Модель Земли задается в гринвичской системе координат EГ. Ее начало координат OГ расположено в центре Земли, ось OГXГ направлена в точку пересечения Гринвичского меридиана с экватором, ось OГZГ совпадает с осью вращения Земли и направлена на Северный полюс Земли, а ось OГYГ дополняет оси до правосторонней системы координат. Таким образом, система EГ перемещается и поворачивается вместе с моделью Земли.
Рассматриваемая модель КА в подсистеме визуализации задается в системе координат EКА,В, которая, как и система EКА, жестко связана с КА. В виртуальной сцене система EКА,В остается неподвижной, а виртуальная камера так же, как и EКА,В, жестко связывается с КА.
Пусть в некоторый момент КА расположен и ориентирован относительно неподвижной системы координат EАГ в соответствии с параметрами, задающими его орбиту, и в камере виден некоторый участок земной поверхности. Задача подсистемы визуализации состоит в том, чтобы в виртуальной сцене установить и ориентировать модель Земли (то есть систему координат EГ) относительно неподвижной модели КА (то есть системы EКА,В) так, чтобы в камере был виден в точности тот же участок Земли. Так как камера жестко связана с КА, математически это условие означает, что любая точка P модели Земли будет иметь в системе EКА,В одни и те же координаты PКА,В независимо от того, будет ли расположена и ориентирована EКА относительно EАГ или EГ относительно EКА,В.
В первом случае, согласно (1), координаты PКА,В можно вычислить следующим образом:
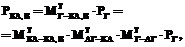 (3)
(3)
где PГ – исходные координаты точки P в системе EГ;  – матрица преобразования координат точки P из системы координат EГ в систему EАГ;
– матрица преобразования координат точки P из системы координат EГ в систему EАГ; 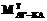 – из EАГ в EКА;
– из EАГ в EКА;  – из EКА в EКА,В. Выражение (3) также можно записать в следующем виде:
– из EКА в EКА,В. Выражение (3) также можно записать в следующем виде:  , где матрица
, где матрица 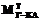 , с одной стороны, определяет результирующее преобразование координат PГ из системы EГ в систему EКА, а с другой – задает положение и ориентацию модели Земли в системе координат EКА. Вычислив
, с одной стороны, определяет результирующее преобразование координат PГ из системы EГ в систему EКА, а с другой – задает положение и ориентацию модели Земли в системе координат EКА. Вычислив 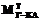 , из нее можно найти вектор переноса и углы Эйлера–Крылова, устанавливающие модель Земли в системе координат EКА, а затем с помощью матрицы
, из нее можно найти вектор переноса и углы Эйлера–Крылова, устанавливающие модель Земли в системе координат EКА, а затем с помощью матрицы  перевести координаты точек модели Земли из системы EКА в систему EКА,В. Рассмотрим эти этапы более подробно.
перевести координаты точек модели Земли из системы EКА в систему EКА,В. Рассмотрим эти этапы более подробно.
 Вычисление матриц преобразования координат точек модели Земли. Согласно выражению (3), чтобы определить координаты любой точки модели Земли в системе координат EКА,В, необходимо вычислить матрицы
Вычисление матриц преобразования координат точек модели Земли. Согласно выражению (3), чтобы определить координаты любой точки модели Земли в системе координат EКА,В, необходимо вычислить матрицы  ,
, 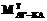 и
и  .
.
Найдем вначале матрицу  . Для этого рассмотрим, как взаимосвязаны системы координат EГ и EАГ. У этих систем оси OГZГ и OАГZАГ совпадают, а часовой угол s между осями OАГXАГ и OГXГ определяется как гринвичское звездное время:
. Для этого рассмотрим, как взаимосвязаны системы координат EГ и EАГ. У этих систем оси OГZГ и OАГZАГ совпадают, а часовой угол s между осями OАГXАГ и OГXГ определяется как гринвичское звездное время: 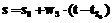 , где s0 – часовой угол (звездное время) в гринвичскую полночь (находится из Астрономического ежегодника); wЗ – угловая скорость вращения Земли;
, где s0 – часовой угол (звездное время) в гринвичскую полночь (находится из Астрономического ежегодника); wЗ – угловая скорость вращения Земли;  – время наступления гринвичской полночи по Москве; t – текущее время по Москве. Согласно (1) координаты PАГ любой точки P модели Земли в системе EАГ находятся как
– время наступления гринвичской полночи по Москве; t – текущее время по Москве. Согласно (1) координаты PАГ любой точки P модели Земли в системе EАГ находятся как
 , то есть
, то есть 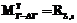 . (4)
. (4)
Матрицу 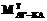 нетрудно найти, приведя соотношение (2) к виду
нетрудно найти, приведя соотношение (2) к виду
 , отсюда
, отсюда
 (5)
(5)
Наконец, из рисунка 3 легко видеть, что система координат EКА совмещается с системой EКА,В поворотом EКА по часовой стрелке сначала вокруг оси OКАZКА на p радиан, а затем вокруг оси OКАYКА на p/2 радиан. Согласно (1) координаты точки P в этих системах соотносятся следующим образом:
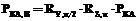 ,
,
то есть 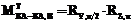 . (6)
. (6)
Подставив (4), (5) и (6) в выражение (3), получим:
 ,
,
где 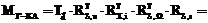 (7)
(7)


 .
.
Восстановление вектора переноса и углов Эйлера–Крылова. Согласно (7) матрицу MГ-КА можно представить в виде произведения двух матриц:
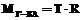 ,
,  ,
, 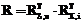
 .
.
Матрица T определяет положение Земли в системе координат EКА, так как она преобразует координаты PГ в координаты PКА, когда система EГ совмещается с системой EКА только путем параллельного переноса. Вектор  является искомым вектором, задающим положение центра Земли в системе EКА.
является искомым вектором, задающим положение центра Земли в системе EКА.
Матрица R задает ориентацию Земли в системе координат EКА, так как она переводит координаты PГ в координаты PКА, когда система EГ совмещается с системой EКА путем последовательных поворотов вокруг своих осей координат.
Чтобы восстановить из матрицы R углы Эйлера–Крылова, задающие ориентацию Земли в системе EКА, представим последовательность поворотов по этим углам в виде матрицы ориентации Земли R¢ и из равенства R¢=R найдем искомые углы Эйлера–Крылова.
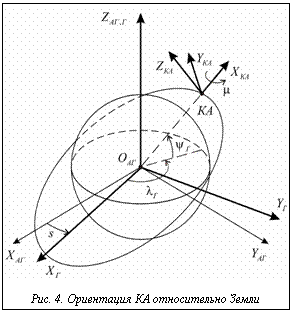
В подсистеме визуализации для ориентации Земли выбирается такая схема поворотов системы EГ на углы Эйлера–Крылова q, y и j, при которой углы j и y сохраняют связь с геоцентрической долготой lГ и широтой yГ положения КА.
Чтобы найти такую схему поворотов, рассмотрим перевод системы координат EГ в систему EКА. Для этого сначала осуществим поворот вокруг оси OГZГ на угол j=-lГ(-p£lГ£p), затем вокруг оси OГYГ, полученной после первого поворота EГ, на угол y=yГ(-p/2£yГ£p/2) и, наконец, вокруг оси OГXГ, полученной после второго поворота EГ, на некоторый угол m (рис. 4). Напомним, что положительным считается поворот по часовой стрелке, если смотреть из конца вектора, вокруг которого осуществляется поворот, чем объясняется знак «–» в выражении j= –lГ. Согласно (1) система EГ переводится в EКА с помощью следующего матричного преобразования:
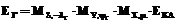 .
.
Из данного выражения получаем:
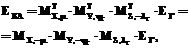 (8)
(8)
что соответствует ориентации системы EГ (жестко связанной с Землей) относительно системы EКА (жестко связанной с КА). Считаем, что углы Эйлера–Крылова – это повороты системы координат вокруг базисных векторов по часовой стрелке, если смотреть из конца вектора, вокруг которого выполняется поворот. Поэтому из (8) получаем следующую схему поворотов по углам Эйлера–Крылова:
· поворот на угол q=–m вокруг оси OКАXКА;
· поворот на угол y=–yГ вокруг оси OКАYКА, полученной после первого поворота EКА;
· поворот на угол j=lГ вокруг оси OКАZКА, полученной после второго поворота EКА.
Согласно (1) из соотношения (8) выводится преобразование координат точки P из системы EКА в систему EГ: 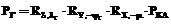 , откуда легко найти, что
, откуда легко найти, что


 .
.
Здесь необходимо отметить, что в случае, когда y=p/2, матрица R¢ принимает следующий вид:
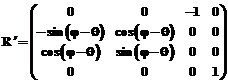 .
.
Как видно, R¢ зависит лишь от разности углов j и q, а не от их конкретных значений, то есть теряется одна степень свободы. Аналогичная ситуация возникает при y=–p/2. Таким образом, при y=±p/2 по матрице невозможно однозначно определить остальные углы Эйлера–Крылова. Будем считать, что рассматриваемая орбита не является полярной (i¹p/2), то есть y¹±p/2 и cosy¹0.
Приравняв R¢ к R, получим следующую систему уравнений:

Отсюда следует:

Знак «+» перед квадратным корнем объясняется тем, что –p/2
Начало.
1. Вычислить угол y:
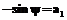 ;
; 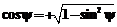 ;
;
 , так как
, так как  .
.
2. Вычислить угол j:
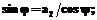
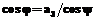 ;
;
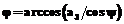 ;
;
Если  , то j = –j.
, то j = –j.
3. Вычислить угол q:
 ;
;  ;
;
 ;
;
Если 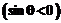 , то q = –q.
, то q = –q.
Конец.
Программируя данный алгоритм, при проверке неравенств необходимо также учесть машинную погрешность представления действительных чисел.
Литература
1. Михайлюк М.В., Торгашев М.А. Система «GLView» визуализации для комплексов виртуального окружения // MEDIAS-2009: тр. Междунар. науч. конф. (10–15 мая 2009 г., Лимассол. Кипр). М.–Протвино: ИФТИ, 2009.
2. Дубошин Г.Н. Справочное руководство по небесной механике и астродинамике. М.: Наука, 1976.
3. Михайлюк М.В., Тимохин П.Ю. Имитация движения космического аппарата по орбите путем моделирования ориентации земной поверхности: сб. тр. М.: НИИСИ РАН, 2009.
4. Meeus J. Astronomical algorithms // Willmann-Bell, 1st Edition, Richmond, Virginia, USA, 1991.
5. Михайлюк М.В. Основы компьютерной графики. М.: МАТИ, 2002.
6. Ken Shoemake. Animating rotation with quaternion calculus. In ACM SIGGRAPH Course Notes 10: Computer Animation: 3-D Motion, Specification, and Control. Anaheim, California, 1987. July 27–31.




 Положение КА в плоскости эллиптической орбиты в момент t задается углом J (истинная аномалия) и длиной r радиус-вектора
Положение КА в плоскости эллиптической орбиты в момент t задается углом J (истинная аномалия) и длиной r радиус-вектора  , направленного из центра Земли в центр масс КА. Вычисление J и r в момент t по заданным параметрам орбиты приводится в [2–4].
, направленного из центра Земли в центр масс КА. Вычисление J и r в момент t по заданным параметрам орбиты приводится в [2–4].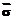 (рис. 1), а ось OСYC дополняет эти оси до правосторонней системы координат (рис. 2). В этой системе координат центр масс КА всегда имеет координаты (r, 0, 0, 1). Введем дополнительную систему координат EКА, жестко связанную с КА, то есть при движении КА координаты его точек в системе EКА не меняются. Начало координат OКА расположим в центре масс КА, а оси координат направим так же, как в системе EС. Тогда положение и ориентацию КА в системе EАГ можно определить, вычислив матрицу преобразования координат точек КА из системы EКА в систему EАГ.
(рис. 1), а ось OСYC дополняет эти оси до правосторонней системы координат (рис. 2). В этой системе координат центр масс КА всегда имеет координаты (r, 0, 0, 1). Введем дополнительную систему координат EКА, жестко связанную с КА, то есть при движении КА координаты его точек в системе EКА не меняются. Начало координат OКА расположим в центре масс КА, а оси координат направим так же, как в системе EС. Тогда положение и ориентацию КА в системе EАГ можно определить, вычислив матрицу преобразования координат точек КА из системы EКА в систему EАГ. и
и 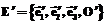 , где
, где  и
и 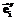 – ортонормированные векторы базисов, а O и O¢ – начала соответствующих систем координат и E переводится в E¢ с помощью произвольной последовательности поворотов и переносов, последовательно совмещаясь с промежуточными системами координат E1,…, Ek-1, то имеют место следующие соотношения:
– ортонормированные векторы базисов, а O и O¢ – начала соответствующих систем координат и E переводится в E¢ с помощью произвольной последовательности поворотов и переносов, последовательно совмещаясь с промежуточными системами координат E1,…, Ek-1, то имеют место следующие соотношения: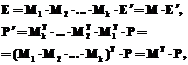 (1)
(1)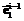 на угол a (
на угол a (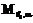 ), или вокруг
), или вокруг 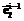 на угол b (
на угол b ( ), или вокруг оси
), или вокруг оси 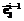 на угол g (
на угол g ( ) (положительным считается поворот системы координат по часовой стрелке, если смотреть с конца вектора, вокруг которого осуществляется поворот), либо путем переноса Ei на вектор
) (положительным считается поворот системы координат по часовой стрелке, если смотреть с конца вектора, вокруг которого осуществляется поворот), либо путем переноса Ei на вектор  (
( ). Матрицы
). Матрицы 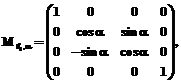



 ,
,  ,
,  и
и  обозначаются в данной статье как
обозначаются в данной статье как 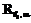 ,
, 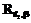 ,
, 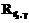 и
и  соответственно.
соответственно.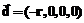 вдоль оси OXКА;
вдоль оси OXКА;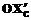 , полученной после первого поворота EС;
, полученной после первого поворота EС;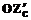 , полученной после второго поворота EС.
, полученной после второго поворота EС.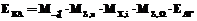 , а преобразование координат PКА в PАГ вид
, а преобразование координат PКА в PАГ вид . (2)
. (2) Как отмечалось ранее, движение КА в подсистеме визуализации имитируется путем переноса и ориентации в виртуальной сцене модели Земли относительно неподвижной модели КА (рис. 3).
Как отмечалось ранее, движение КА в подсистеме визуализации имитируется путем переноса и ориентации в виртуальной сцене модели Земли относительно неподвижной модели КА (рис. 3).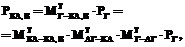 (3)
(3) – матрица преобразования координат точки P из системы координат EГ в систему EАГ;
– матрица преобразования координат точки P из системы координат EГ в систему EАГ; 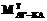 – из EАГ в EКА;
– из EАГ в EКА;  – из EКА в EКА,В. Выражение (3) также можно записать в следующем виде:
– из EКА в EКА,В. Выражение (3) также можно записать в следующем виде:  , где матрица
, где матрица 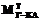 , с одной стороны, определяет результирующее преобразование координат PГ из системы EГ в систему EКА, а с другой – задает положение и ориентацию модели Земли в системе координат EКА. Вычислив
, с одной стороны, определяет результирующее преобразование координат PГ из системы EГ в систему EКА, а с другой – задает положение и ориентацию модели Земли в системе координат EКА. Вычислив  Вычисление матриц преобразования координат точек модели Земли. Согласно выражению (3), чтобы определить координаты любой точки модели Земли в системе координат EКА,В, необходимо вычислить матрицы
Вычисление матриц преобразования координат точек модели Земли. Согласно выражению (3), чтобы определить координаты любой точки модели Земли в системе координат EКА,В, необходимо вычислить матрицы 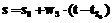 , где s0 – часовой угол (звездное время) в гринвичскую полночь (находится из Астрономического ежегодника); wЗ – угловая скорость вращения Земли;
, где s0 – часовой угол (звездное время) в гринвичскую полночь (находится из Астрономического ежегодника); wЗ – угловая скорость вращения Земли;  – время наступления гринвичской полночи по Москве; t – текущее время по Москве. Согласно (1) координаты PАГ любой точки P модели Земли в системе EАГ находятся как
– время наступления гринвичской полночи по Москве; t – текущее время по Москве. Согласно (1) координаты PАГ любой точки P модели Земли в системе EАГ находятся как , то есть
, то есть 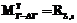 . (4)
. (4) , отсюда
, отсюда (5)
(5)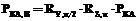 ,
,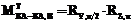 . (6)
. (6) ,
,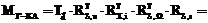 (7)
(7)

 .
.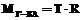 ,
,  ,
, 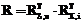
 .
. является искомым вектором, задающим положение центра Земли в системе EКА.
является искомым вектором, задающим положение центра Земли в системе EКА.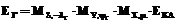 .
.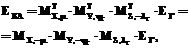 (8)
(8)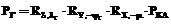 , откуда легко найти, что
, откуда легко найти, что

 .
.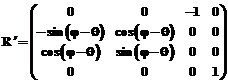 .
.

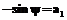 ;
; 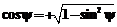 ;
; , так как
, так как  .
.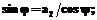
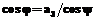 ;
;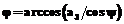 ;
; , то j = –j.
, то j = –j. ;
;  ;
; ;
;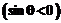 , то q = –q.
, то q = –q.