Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Комбинаторные методы восстановления функций по их усреднениям на дискретных подмножествах области определения
Аннотация:Рассматривается задача вычисления значений функции, определенной на счетном дискретном носителе, в каждой точке ее области определения, если известны только средние значения на достаточно большом наборе конечных или счетных подмножеств. Эта задача аналогична задаче интегральной геометрии на континуальных пространствах с мерой, однако дискретность носителя функционального пространства позволяет получить новые комбинаторные методы обращения усредняющих операторов, не сводимые к известным формулам обращения в интегральной геометрии. Методы можно применять к пространствам с различной дискретной математической структурой.
Abstract:It considered the task of computing the value of function (which is determent on countable discrete support) for each point in domain of definition, if it is known only average value of that function on sufficiently big assembly of finite or countable subsets. That task is analogous the integral geometry task on continuality spaces with measure. But the discrete support of functional space permit to obtain new combinatorial methods for inversion of average operators, which are not reducible to known formulas in integral geometry. Those methods may by apply on spaces with different mathematical structures.
| Авторы: Граев М.И. (akoganov@yandex.ru) - НИИСИ РАН, Москва, доктор физико-математических наук, Коганов А.В. (koganow@niisi.msk.ru) - НИИСИ РАН, г. Москва, кандидат физико-математических наук | |
| Ключевые слова: двойное разбиение, усреднение на группе, интегральная геометрия, формула обращения |
|
| Keywords: dual subdivision, average on group, integral geometry, inversion formula |
|
| Количество просмотров: 12157 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
Классическая интегральная геометрия (начиная с работ И.М. Гельфанда) рассматривает интегральные преобразования, относящие измеримым функциям, определенным на том или ином многообразии, их интегралы по некоторому семейству его подмногообразий (например, преобразование Радона на плоскости, относящее функциям на плоскости их интегралы по всевозможным прямым [1–3]). Основная задача состоит в описании образов и ядер этих преобразований и, главное, в построении формулы обращения, которая восстанавливает исходную функцию по ее преобразованию. Идеи и результаты интегральной геометрии используются в других разделах математики и в ее приложениях, в частности, в медицинской томографии. В постановке задач интегральной геометрии исходные объекты (многообразия) могут быть заменены объектами иной природы, например, дискретными комбинаторными множествами или графами [3–5]. Это приводит к новому циклу задач, интересных не только внутри математики, но и в приложениях. В данной статье рассматриваются некоторые простейшие задачи, связанные с дискретными множествами. Для краткости назовем их задачами усреднения, а возникающие в них преобразования – операторами усреднения. В общей постановке задача усреднения может быть сформулирована следующим образом. Заданы конечное или счетное множество X и набор Y подмножеств этого множества. Оператор усреднения ставит в соответствие каждой числовой функции, определенной на X, суммы ее значений по элементам каждого подмножества из совокупности Y. Если значения некоторой функции на X образуют абсолютно сходящийся ряд, то ее суммы образуют функцию на Y. Требуется найти условия, при которых исходная функция на X может быть восстановлена по соответственной функции на Y, и получить для этого явную формулу обращения. Отметим, что в такой постановке задачи самому понятию «усреднение» можно придать обобщенный смысл (например, усреднение с весами). Кроме того, можно предполагать, что само мно- жество X и область значений функций на нем снабжены дополнительной структурой (например, частичным порядком или специальным действием некоторой группы). Таким образом, исходное определение оператора усреднения имеет много разных вариантов. Двойные разбиения Пусть A и B – произвольные счетные абстрактные множества, а CÌA´B – фиксированное подмножество пар (a, b), где aÎA и bÎB; Определение. Положим, что CÌA´B задает двойное разбиение и будем писать (A¬C®B), если Ab¹Æ для всех bÎB, Ab¹Ab¢ при b¹b¢ и В силу этого определения множество B можно рассмотреть с точностью до биекции как набор попарно различных подмножеств AbÌA. Аналогично множество A может быть интерпретировано как набор попарно различных подмножеств BaÌB. Свяжем с каждым двойным разбиением (A¬C®B) следующую задачу усреднения. Обозначим для произвольного не более чем счетного множества V через H(V) пространство всех вещественных или комплекснозначных функций f(×) на V, удовлетворяющих условию абсолютной суммируемости: Поставим в соответствие каждой функции fÎH(A) функцию If(×) на B:
Предложение. Если для любого bÎB число элементов #Ab не превосходит k<¥, то из условия fÎH(A) следует, что IfÎH(B). В общем случае это необязательное свойство. Задача: восстановить исходную функцию fÎH(A) по функции IfÎH(B). Рассмотрим подходы к решению этой задачи при различных дополнительных условиях на двойные разбиения. Неособые точки двойных разбиений. Пусть (A¬C®B) – произвольное двойное разбиение. Определение. Назовем точку aÎA неособой, если для любого конечного подмножества
В противном случае назовем aÎA особой точкой множества A. Теорема 1. Для любой неособой точки a0 двойного расслоения существует формула обращения, восстанавливающая f(a)ÎH(A) по j(b). Доказательство. Занумеруем произвольным образом элементы множества A=(a0, a1, …). Поскольку a0 – неособая точка, то для любого натурального числа n существует такой элемент bnÎB, что a~bn и aiØ~bn, i=1, …, n. Тогда для любой функции f(a)ÎH(A) справедлива следующая формула обращения:
Действительно, частичные суммы этого ряда равны: Замечание. Имеется тривиальный частный случай теоремы, когда для некоторого aÎA имеется такое bÎBa, что Ab={a}. Иными словами, точка имеет инцидентное подмножество, состоящее только из нее самой. Тогда, по определению, точка a неособая, даже если нет других инцидентных ей подмножеств. И в этом случае формула (1) вырождается в f(a)=j(b), где уже нет бесконечной суммы или предельного перехода. В качестве последовательности {bi} можно взять bi=b. Этот пример показывает, что неособые точки могут иметь конечное число инцидентных подмножеств. Но это нехарактерный случай. Частные случаи двойных разбиений. Рассмотрим примеры двойных разбиений (A¬C®B), у которых все точки неособые. Далее для удобства изложения элементы из A будем называть точками, а элементы из B – подмножествами. Это соответствует сделанному выше замечанию об интерпретации B«{Ab½bÎB}. Лемма 1. Пусть двойное разбиение удовлетворяет следующим аксиомам. 1. Для каждой пары точек существует одно и только одно подмножество, инцидентное им обеим: 2. Для каждой точки существует бесконечно много инцидентных ей подмножеств: "aÎA #Ba=¥. Тогда все точки неособые. Доказательство. Пусть заданы произвольная точка aÎA и такое конечное множество VÌA, #V<¥, что aÎA\V. Обозначим Лемма 2 (усиление леммы 1). Условие 1 заменяется на более слабое. 1м) Для каждой пары точек существует не более чем одно подмножество, инцидентное им обеим:
Условие 2 сохраняется. Тогда все точки неособые. Доказательство повторяет доказательство леммы 1 с заменой определения b(a, a¢)=b, если такое подмножество есть (тогда оно единственно по условию 1м), либо b(a, a¢)=Æ, если такого подмножества нет. Пример 1 (соответствует лемме 1). A= Пример 2 (соответствует лемме 2). Рассмотрим многомерную целочисленную сеть Данный пример имеет важное обобщение. Лемма 3. При любой размерности n сети Пример 3 (соответствует лемме 2). Оба множества определяются одинаково:
являясь множеством пар взаимно простых целых чисел. Две пары инцидентны (x, y)~(u, v), если xv–yu=1. Это означает, что для любой пары инцидентная ей пара задает соответственные коэффициенты линейной комбинации, выявляющей взаимную простоту компонент. Тогда пара из класса подмножеств инцидентна двум парам из класса точек, если верны два уравнения (x, y)~(u, v) & (p, q)~(u, v) Û xv–yu=1 & pv–qu=1. Такое целочисленное решение u, v существует не для всех двоек (x, y), (p, q). Но если решение есть, то два числа однозначно определены двумя линейными уравнениями. Лемма 4 (обобщение лемм 1 и 2). Задача усреднения разрешима в любой точке aÎA, для которой существует последовательность инцидентных подмножеств biÎB, a~bi, i=0, 1, … , в которой biÇbj={a}, i¹j. Формула обращения совпадает с формулой (1). Допустимые подмножества и связанные с ними формулы обращения. Формула обращения (1) для преобразования If функций f из H(A) применима только при восстановлении функций в неособых точках aÎA, и возникает задача о восстановлении функций в особых точках. Такая задача может не иметь решения, а потому заменяем ее на более общую задачу, которая здесь будет рассмотрена: восстановить по функции If сумму значений исходной функции f на некотором фиксированном подмножестве DÌA. Такое восстановление будем называть условным обращением преобразования усреднения. Определение. Назовем подмножество DÌA в двойном разбиении (A¬C®B) допустимым, если для каждого конечного подмножества MÌA\D существует элемент bÎB, инцидентный всем элементам aÎD и не инцидентный ни одному элементу из M. В частности, само множество A всегда допустимо, а одноэлементное подмножество {a}, aÎA допустимо тогда и только тогда, когда точка a неособая. Теорема 2. Для каждого допустимого подмножества DÌA имеет место следующая формула условного обращения для преобразования I на H(A):
где biÎB – элемент, инцидентный всем aÎD и не инцидентный (как минимум) первым i элементам множества A\D при любом фиксированном упорядочении элементов этого множества. Вывод формулы (2) совпадает с выводом формулы обращения (1). Отметим, что в простейшем случае, когда множество A\D конечно, в соответствии с определением допустимости существует такой элемент bÎB, что Ab=D. Тогда формулу (2) можно представить в тривиальной форме: Sf(D)=j(b). Заметим также, что каждое подмножество Ab, bÎB является допустимым и Sf(Ab)=j(b). (3) Определение. Назовем допустимое подмножество DÌA приклеенным к точке a, если aÎD. Назовем точку aÎA слабо неособой, если существует приклеенное к a допустимое подмножество DÌA, в котором все точки, отличные от a, неособые. В частности, если aÎA – единственная особая точка, то, поскольку множество A допустимо, она является слабо неособой. Утверждение. Для каждой слабо неособой точки a существует формула обращения:
В правой части первый член определяется по формуле (2), а каждый член второй суммы – по (1). Дадим рекуррентное определение неособой точки глубины n, n=0, 1, 2, … . Определение. Неособая точка имеет глубину 0. Неособая точка aÎA глубины n, n>0, принадлежит допустимому множеству DÌA, в котором все точки, кроме a, являются неособыми точками глубины, меньшей n, а сама точка a не относится к этому классу. В частности, определенная выше слабо неособая точка имеет глубину 1. Обозначим для неособой точки xÎA конечной глубины ее глубину как n(x). Теорема 3. Для каждой неособой точки a конечной глубины n существует формула обращения. Пусть для точек xÎA всех глубин n(x)
Доказательство по индукции. Для n(a)=0 имеется оператор обращения, заданный уравнением (1). Для n(a)=1 формула (4) соответствует общему виду (5). Предположим, что формула обращения (5) верна для всех n(x) Эта теорема значительно расширяет класс точек, где можно восстановить функцию по усреднениям. При этом требуется следующая последовательность действий. Вначале восстанавливаются значения в неособых точках, потом – в слабо неособых точках и далее – в порядке роста глубины. Для счетных бесконечных множеств вычисления пределов и сумм рядов делаются приближенно с нужной точностью. Это возможно, если fÎH(A). Пример 4. Множество точек A= Система подмножеств B= Отношение инцидентности (x, 1)~[y, 1, n]Û Û$iÎ Тогда Для m³2 определим (x, m)~[y, m¢, 1]Ûx=y; m¢=m, m+1. Тогда A[y, m, 1]={(y, m); (y, m–1)}, m³2. Подмножества [y, m, n], n³2, не имеют инцидентных точек: A[y, m, n]=Æ, m³2, n¹1. Иными словами, модель имеет слои, пронумерованные индексом m=1, …, и на первом слое точка инцидентна всем проходящим через нее арифметическим прогрессиям с натуральной разностью и двусторонним индексом, а на других слоях точка инцидентна паре из себя и такой же точке на предыдущем слое. Все точки первого слоя неособые. Действительно, если задано произвольное конечное подмножество MÌA, то имеется x(M)=max{½x½½(x, m)ÎM}. Для точки (x, 1) инцидентное подмножество [x, 1,½x–x(M)½]ÎB не содержит ни одной точки из M\{(x, 1)}. Тогда точки второго слоя (x, 2) неособые глубины 1. В качестве допустимого множества можно взять подмножество [x, 2, 1]ÎB. Аналогично точки любого слоя m>2 являются неособыми глубины m–1 с допустимым подмножеством [x, m, 1]ÎB. Таким образом, пространство A имеет неособые точки любой глубины, и на H(A) оператор усреднения обратим по рекуррентной формуле (5), которая в данном случае упрощается, поскольку приклеенные допустимые множества двухэлементные:
N-разбиения Определение. Пусть задано N-разбиение, ес- ли задана последовательность N счетных множеств A1, …, AN, и с каждой парой соседних множеств Ak, Ak+1 из этой последовательности связано двойное разбиение (Ak¬Ck®Ak+1), где CkÌAk´Ak+1. Определение. Порожденным двойным разбиением (Ak¬Ck,l®Al), k
Для N-разбиения определены все операторы усреднения на компонентах N-разбиения, которые действуют на пространствах H(Ak), k=1, …, N–1:
где скобки внизу показывают, к какому множеству Ak принадлежит элемент, а индекс у функции указывает на ее принадлежность к H(Ak). Заметим, что это преобразование действует только на соседних по индексу множествах. Если применить усреднение для порожденного двойного разбиения при l–k>1, то формула (6) не будет соответствовать порожденной инцидентности. Кроме того, итерация усреднений может оказаться невыполнимой, если образ функции выйдет из H(Ak+1). Обозначим оператор усреднения по порожденному 2-разбиению (A1¬C1,l®Al), 1
Введем оператор частичного усреднения функции на Ak по подмножеству VÌAk:
Область определения этой функции Определение. Назовем N-разбиение транзитивным, если выполнены следующие условия. 1а. Для каждого x(k)ÎAk существует такое подмножество V=Vk(x(k))ÌAk, что
2а. Совокупность значений (x(k+1), f*k+1(x(k+1))), x(k+1)ÎD[V] достаточна для применения некоторой формулы обращения при восстановлении значения f*k(x(k)). Теорема 4. Для транзитивного N-разбиения транзитивное усреднение обратимо. Доказательство. По условию 2а имеется оператор, который в любой точке x(k) восстанавливает значение f*k(x(k)) по известным значениям Эта теорема имеет принципиальное следствие. Теорема 5. При любой размерности n сети Этот результат обобщает на случай целочисленных решеток любых размерностей известную теорему [6] о наличии формул обращения для аналогичных интегральных операторов на элементах грассманиана в Доказательство. Для того чтобы использовать формулу обращения (1) при восстановлении значения функции на К-плоскости по усреднению ее значений на (К+1)-плоскостях в Заметим, что формула (1) в данном случае содержит бесконечный ряд или предельный переход. Это означает, что практически провести восстановление значений усреднения с понижением размерности можно в общем случае только приближенно. Задачи, связанные с подгруппами счетных дискретных групп Резольвентные подгруппы. (Термин «резольвентный» предложен И.М. Гельфандом.) Пусть A – произвольная дискретная счетная группа и G – собственная счетная подгруппа группы A. Свяжем с парой (G, A) двойное разбиение (A¬C®B), где B – совокупность всех двусторонних классов смежности подгруппы G в группе A, то есть подмножеств в A вида b=a1Ga2; a1, a2ÎA; отношение инцидентности a~b – принадлежность элемента aÎA классу смежности b. Условимся называть такие двойные разбиения связанными с группой A и ее подгруппой G и коротко обозначать через [G, A]. Заметим, что классами сопряженных элементов, инцидентными единичному элементу eÎA, являются подгруппы aGa-1, сопряженные с подгруппой G. Очевидно, что для каждого двойного разбиения [G, A] все точки aÎA являются одновременно особыми или неособыми. Определение. Назовем подгруппу G группы A резольвентной, если для связанного с парой [G, A] двойного разбиения отображение, относящее функциям fÎH(A) их образы If, обратимо во всех точках aÎA. Назовем подгруппу G группы A строго резольвентной, если все точки aÎA в двойном разбиении [G, A] являются неособыми или, что эквивалентно, неособой точкой является единичный элемент eÎA. Очевидно, что любая подгруппа строго резольвентной группы также строго резольвентна. Примерами нестрого резольвентных подгрупп являются все группы GÌ~A, для которых пересечение GÇZ, где Z – центр группы A, отлично от единичной группы. В этом случае любая подгруппа, сопряженная с Z, содержит все элементы из GÇZ. На основании теоремы 1 любая строго резольвентная подгруппа является резольвентной, и для нее обращение преобразования I может быть за- дано формулой (1). Вопрос о том, следует ли обратно условие строгой резольвентности из условия резольвентности, требует отдельного обсуждения. Примеры строго резольвентных подгрупп. Пусть группа A относится к любому из двух классов: SL(n, Пример 5. Пусть G – подгруппа всех нижних треугольных матриц с единицами на диагонали, то есть подгруппа матриц êêgi,júú, у которых gi,j=0 при i Легко убедиться, что у матрицы Строгая резольвентность подгруппы G определяется на основании теоремы 1 из следующего утверждения. Лемма 5. Для каждого отличного от единичного элемента x=úúxi,júú группы G имеем Доказательство. Обозначим y=
где положено xn+1,j=0. В силу этого равенства xi,j входит слагаемым в выражение для yi,n с коэффициентом an-j, где n-j>0. Отсюда следует, что yi,n®¥ при a®¥, а потому yÏG при достаточно большом a. Лемма доказана. Заметим, что подгруппа в GL(n, Пример 6. Пусть G – группа SL(n-1, Докажем, что эти подгруппы также строго резольвентны. Условимся представлять элементы исходных групп в блочной форме: Нужно убедиться, что для любого конечного множества X элементов исходной группы Введем множество элементов h исходной группы вида Из определения матриц h следует:
где e – единичная матрица. Введем два дизъюнктных подмножества в X:
Обозначим через H множество всех таких векторов r, что rbi¹0 при giÎX1, r(ai–di)¹0 при giÎX2, и примем s=rT (транспонированный вектор). Легко убедиться, что множество H непусто и содержит вместе с каждым вектором r все векторы nr. Покажем, что h-1gihÏG, i=1, …, N, при достаточно большом r. В самом деле, если giÎX1, то из выражения для di следует, что при большом r оно становится сколь угодно большим, а потому h-1gihÏG при большом r. То же самое справедливо на основании выражения для gi в случае giÎX2. Если, наконец, giÎX1\X2, то gi=ci. Значит, h-1gihÏG, если ci¹0. В случае ci=0 матрица gi скалярна. Тогда h-1gihÏG, кроме случая gi=e, который исключается. Утверждение доказано. Задачи, связанные с решетками над счетными дискретными кольцами Постановка общей задачи. Пусть L – произвольное счетное, необязательно коммутативное кольцо. Двойное разбиение (A¬C®B) свяжем с произвольным полиномом P(a, x) над L от символов a=(a1, …,am) и x=(x1, …, xn). Определение. Назовем элементы aÎLm и xÎLn инцидентными и будем писать a~x, если для них P(a, x)=0. Введенное отношение инцидентности задает двойное разбиение, где C – множество инцидентных пар; A и B – проекции C на aÎLm и xÎLn соответственно. Естественно предположить, что множество C не пусто. Отметим специальный случай двойного разбиения. Пусть p(x) – такой произвольный полином над L от x=(x1, …, xn), что уравнение p(x)=0 имеет хотя бы одно решение в xÎLn. Определим двойное разбиение, связанное с полиномом p(x), как разбиение, связанное с полиномом P(a, x)=p(a–x). Очевидно, что у этого разбиения A=B=Ln и для всех точек xÎLn число инцидентных с ними точек одно и то же. Поэтому все подобные двойные разбиения распадаются на классы по числу инцидентных точек. Исследуем простейшие примеры таких двойных разбиений. Для анализа нам потребуется следующий факт. Пусть на счетном множестве A задано двойное разбиение с #B=#A. Имеется биективное отображение h:A«B. Отношение инцидентности сопоставляет каждому aÎA подмножество h(a)=bÎB, причем Ab={a}ÈMa. Тогда оператор усреднения можно записать в форме
Тогда Эта формула позволяет проводить итерацию, подставляя вместо каждого члена последней суммы его выражение такого вида. Лемма 6. Допустим, все множества Ma заданы так, что при бесконечном повторении итерации формулы (7) каждый элемент xÎA, x¹a, встретится в сумме не более S раз (конечное число). Тогда для функции fÎH(A) преобразование усреднения обратимо, а асимптотическая формула обращения в каждой точке задается неограниченной итерацией формулы (7). Доказательство. По условию при неограниченной итерации из суммы за счет вычитания бу- дут навсегда удалены точки, которые уже возникали S раз. Таким образом, для любого конечного набора точек, который не содержит точку a, можно указать номер итерации, после которого эти точки уже не появятся. Поскольку fÎH(A), то Пример 7. Операция усреднения функций на A имеет вид: Очевидно, что в этом примере через каждую точку проходит счетное множество прямых. Отметим, что через каждую пару точек (x1, x2) и (x¢1, x¢2) проходит не более одной прямой и условием прохождения прямой через эти точки является равенство x1x¢2=x2x¢1=±1. По лемме 2 оператор усреднения обратим. Пример 8. p(x, a)=xa–c, c>0, x,aÎ Отношение инцидентности между этими парами имеет вид (x1, x2)~(a1, a2)Û(a1–x1)(a2–x2)=c. Таким образом, число элементов aÎB, инцидентных xÎA, и, соответственно, число элементов xÎA, инцидентных aÎB, конечно и равно числу k разложений c в произведение положительных и отрицательных целых сомножителей. В частности, при c=1, 2, 3, 4 имеем соответственно k=2, 2, 2, 4. Назовем это число k типом рассматриваемого разбиения. Для этого двойного разбиения операция усреднения имеет следующий вид:
В данной сумме можно выделить член с минимально возможной координатой p= –c при q= –1. Сумму запишем относительно приращений (p¢, q¢) к этой точке:
В настоящей формуле существенно, что p¢>0 для всех точек суммирования. Отсюда следует, что в пространстве абсолютно суммируемых функций f на Пример 9. p(x, y)=x2+y2–c2. Условие инцидентности (x, y)~(a, b)Û(a–x)2+ +(b–y)2=c2. Известно, что эти подмножества непусты тогда и только тогда, когда c представимо в виде суммы квадратов целых чисел: c=p2+q2. Таким образом, число элементов aÎB, которые инцидентны xÎA, и, соответственно, число элементов xÎA, инцидентных aÎB, конечное и равно числу k указанных разложений c. Именно каждой такой паре чисел (p, q) отвечает с точностью до перестановки решение x=2pq, y=p2–q2. В частности, k=4 при c=1 и c=2, k=12 при c=5 и т.д. Это число k также назовем типом 2-разбиения. Пусть Тогда для этого двойного разбиения операцию усреднения функций fÎH(A) можно представить в виде Аналогично предыдущему примеру по лемме 6 этот оператор обратим для абсолютно суммируемых функций f и существует явная формула обращения для этого преобразования. На основании изложенного можно сделать следующие выводы. Свойство дискретности носителя для пространства функций позволяет сформулировать эффективные требования к системе множеств усреднения, которые гарантируют наличие формул обращения. Характерным видом формул обращения в рассмотренном случае является предел некой последовательности или бесконечного ряда, которые в конечных пространствах имеют конечное число членов. В конечном случае конструктивны формулы обращения (иногда тривиальны), а в бесконечном – вычисления с заданной точностью. Имеются многочисленные примеры из разных разделов математики, таких как теория графов, теория групп, теория колец, в которых применимы найденные формулы обращения для усреднения на естественных системах подмножеств в соответствующих структурах. Литература 1. Гельфанд И.М., Граев М.И., Виленкин Н.Я. Обобщенные функции. Интегральная геометрия и связанные проблемы теории представлений. М.: Физматгиз, 1962. Т. 5. 2. Гельфанд И.М., Гиндикин С.Г., Граев М.И. Избранные задачи интегральной геометрии. М.: Добросвет, 2000. 208 с. 3. Граев М.И., Коганов А.В. Алгоритмы восстановления функции через ее усреднения по подмножествам // Программные продукты и системы. 2008. № 4. С. 33–38. 4. Коганов А.В. Комбинаторные методы интегральной геометрии//Математика. Компьютер. Образование. М.–Ижевск: НИЦ «Регулярная и хаотическая динамика». Вып. 12. Ч. 2. 2005. С. 746–758. 5. Коганов А.В. Интегральная геометрия на системах покрытий // Математические исследования: сб. тр. [под ред. В.Б. Бетелина]. НИИСИ РАН, 2005. С. 197–230. 6. Граев М.И. Относительно замкнутые операторы, связанные с парой грассманианов. Математические заметки. M.: Наука, 2002. Т. 71. Вып. 1. С. 61–74. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2609 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



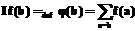 . Назовем элементы aÎA и bÎB инцидентными и будем писать a~b, если (a, b)ÎC. Обозначим Ab={a½a~b}ÌA, Ba={b½a~b}ÌB.
. Назовем элементы aÎA и bÎB инцидентными и будем писать a~b, если (a, b)ÎC. Обозначим Ab={a½a~b}ÌA, Ba={b½a~b}ÌB. ; аналогично Ba¹Æ для всех aÎA, Ba¹Ba¢ при a¹a¢ и
; аналогично Ba¹Æ для всех aÎA, Ba¹Ba¢ при a¹a¢ и 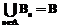 .
. .
. .
. существует элемент b(a/A¢)ÎB, инцидентный a, но не инцидентный ни одному элементу a¢ÎA¢:
существует элемент b(a/A¢)ÎB, инцидентный a, но не инцидентный ни одному элементу a¢ÎA¢: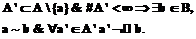
 . (1)
. (1)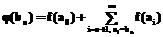 . С ростом n последняя сумма стремится к 0 в силу определения H(A). Конец доказательства.
. С ростом n последняя сумма стремится к 0 в силу определения H(A). Конец доказательства. . Далее это подмножество обозначим b=b(a, a¢).
. Далее это подмножество обозначим b=b(a, a¢). . По условию 2 A\W¹Æ. Тогда для любого a¢ÎA\W выполнено условие VÇAb(a, a¢)=Æ. Но по определению a!~b(a, a¢). Условие неособенной точки выполнено. Лемма доказана.
. По условию 2 A\W¹Æ. Тогда для любого a¢ÎA\W выполнено условие VÇAb(a, a¢)=Æ. Но по определению a!~b(a, a¢). Условие неособенной точки выполнено. Лемма доказана.
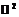 = ={(x, y)½x, yÎ
= ={(x, y)½x, yÎ } – множество точек с целыми координатами на координатной плоскости. B – множество прямых вида ax+bx=c с целыми коэффициентами a, b, c на той же координатной плоскости. Отношение инцидентности – принадлежность точки прямой.
} – множество точек с целыми координатами на координатной плоскости. B – множество прямых вида ax+bx=c с целыми коэффициентами a, b, c на той же координатной плоскости. Отношение инцидентности – принадлежность точки прямой. , n>2. Определим A как множество целочисленных прямых на этой сети, а множество B – как множество целочисленных плоскостей там же. Инцидентность по принадлежности прямой плоскости. Ясно, что выполняется условие леммы 2. Следовательно, усреднения функций от коэффициентов прямой по плоскостям обратимы на этой сети.
, n>2. Определим A как множество целочисленных прямых на этой сети, а множество B – как множество целочисленных плоскостей там же. Инцидентность по принадлежности прямой плоскости. Ясно, что выполняется условие леммы 2. Следовательно, усреднения функций от коэффициентов прямой по плоскостям обратимы на этой сети. обратимы усреднения функций от наборов параметров целочисленных К-плоскостей (в качестве точек) по всем целочисленным (К+1)-плоскостям (в качестве подмножеств). Отношение инцидентности задается по вложению К-плоскости в (К+1)-плоскость. Доказательство сразу следует из леммы 2, поскольку для двух различных К-плоскостей есть инцидентная им (К+1)-плоскость только в случае, если у них пересечение по (К-1)-плоскости, и в этом случае объемлющая их (К+1)-плоскость натянута на совокупность их направляющих векторов, а это определяет ее однозначно.
обратимы усреднения функций от наборов параметров целочисленных К-плоскостей (в качестве точек) по всем целочисленным (К+1)-плоскостям (в качестве подмножеств). Отношение инцидентности задается по вложению К-плоскости в (К+1)-плоскость. Доказательство сразу следует из леммы 2, поскольку для двух различных К-плоскостей есть инцидентная им (К+1)-плоскость только в случае, если у них пересечение по (К-1)-плоскости, и в этом случае объемлющая их (К+1)-плоскость натянута на совокупность их направляющих векторов, а это определяет ее однозначно. ,
, (2)
(2)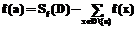 . (4)
. (4)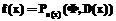 , где D(x) – допустимое множество для точки xÎA, а символ F обозначает совокупность значений оператора усреднения
, где D(x) – допустимое множество для точки xÎA, а символ F обозначает совокупность значений оператора усреднения  . Тогда D(a)=D, n(a)=n и оператор обращения для точки a имеет вид
. Тогда D(a)=D, n(a)=n и оператор обращения для точки a имеет вид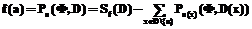 . (5)
. (5) ´
´ ={(x, n)½xÎ
={(x, n)½xÎ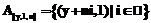 .
.
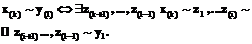
 , (6)
, (6) , f(×)=f*1(×).
, f(×)=f*1(×).
 состоит из тех x(k+1)ÎAk+1, для которых множество членов суммы в определении не пусто. Этот домен зависит только от выбранного подмножества и одинаков для всех функций.
состоит из тех x(k+1)ÎAk+1, для которых множество членов суммы в определении не пусто. Этот домен зависит только от выбранного подмножества и одинаков для всех функций. .
. . Выбрав точку x(k-1) и построив для нее по условию 1а множество
. Выбрав точку x(k-1) и построив для нее по условию 1а множество  , получим D[(x(k-1))]ÌAk. Вычислив значения f*k(y) в каждой точке yÎD[x(k-1)], можно перейти к значению f*k-1(x(k-1)). Продолжая этот процесс, получим любое значение вида f*i(y), 1£i£k, yÎAi. Теорема доказана.
, получим D[(x(k-1))]ÌAk. Вычислив значения f*k(y) в каждой точке yÎD[x(k-1)], можно перейти к значению f*k-1(x(k-1)). Продолжая этот процесс, получим любое значение вида f*i(y), 1£i£k, yÎAi. Теорема доказана. множества К-плоскостей, K=0, 1, …, n, образуют транзитивную n-систему. Возможно восстановление усреднений на К-плоскостях по значениям усреднений на М-плоскостях при 0£K
множества К-плоскостей, K=0, 1, …, n, образуют транзитивную n-систему. Возможно восстановление усреднений на К-плоскостях по значениям усреднений на М-плоскостях при 0£K . Однако структура формул обращения в дискретном случае совершенно иная.
. Однако структура формул обращения в дискретном случае совершенно иная.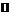 ) всех невырожденных матриц порядка n, n³2, с рациональными элементами. Для каждой из них будут определены две строго резольвентные подгруппы G.
) всех невырожденных матриц порядка n, n³2, с рациональными элементами. Для каждой из них будут определены две строго резольвентные подгруппы G.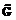 подгруппу всех верхних треугольных матриц. У ее элементов на диагонали стоят числа ±1 в случае группы SL(n,
подгруппу всех верхних треугольных матриц. У ее элементов на диагонали стоят числа ±1 в случае группы SL(n,  есть единичная подгруппа. Свяжем с каждым целым числом a матрицу gaÎ
есть единичная подгруппа. Свяжем с каждым целым числом a матрицу gaÎ , обратной к ga, элементы над ее диагональю суть
, обратной к ga, элементы над ее диагональю суть  .
. при достаточно большом a.
при достаточно большом a. . Если x – любая верхняя треугольная матрица, отличная от единичной, то y есть матрица того же вида, а потому yÎG при любом a. Поэтому достаточно ограничиться случаем, когда существует элемент xi,j¹0 с индексами i>j. Воспользуемся тем, что элементы матрицы y выражаются через элементы матрицы x следующим равенством:
. Если x – любая верхняя треугольная матрица, отличная от единичной, то y есть матрица того же вида, а потому yÎG при любом a. Поэтому достаточно ограничиться случаем, когда существует элемент xi,j¹0 с индексами i>j. Воспользуемся тем, что элементы матрицы y выражаются через элементы матрицы x следующим равенством: ,
, .
.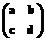 , где диагональные элементы a и d – матрицы порядков n и 1 соответственно. В этих обозначениях G – суть подгруппа матриц вида
, где диагональные элементы a и d – матрицы порядков n и 1 соответственно. В этих обозначениях G – суть подгруппа матриц вида  .
.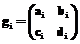 , i=1, …, N, не содержащего единичный элемент, существует такой элемент h исходной группы, что h-1gihÏG, i=1, …, N.
, i=1, …, N, не содержащего единичный элемент, существует такой элемент h исходной группы, что h-1gihÏG, i=1, …, N.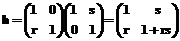 , где r=(r1, …,rn), s=(s1, …, sn) – вектор-строка и вектор-столбец с целыми и, соответственно, рациональными элементами, и обозначим для каждого из них
, где r=(r1, …,rn), s=(s1, …, sn) – вектор-строка и вектор-столбец с целыми и, соответственно, рациональными элементами, и обозначим для каждого из них  .
. ,
, ,
,
 .
. . (7)
. (7) . Отсюда следует, что с ростом номера итерации сумма значений f(x), добавленная к знакопеременному ряду значений If(h(x)) в правой части результирующей формулы, стремится к 0. Лемма доказана.
. Отсюда следует, что с ростом номера итерации сумма значений f(x), добавленная к знакопеременному ряду значений If(h(x)) в правой части результирующей формулы, стремится к 0. Лемма доказана. P(a, x)=a1x2–a2x1–1 над кольцом
P(a, x)=a1x2–a2x1–1 над кольцом  .
.
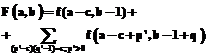
 . Соответствующий y имеет вид
. Соответствующий y имеет вид 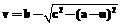 .
.