Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программный комплекс анализа структурного сходства систем с учетом расположения фрагментов
Аннотация:Рассмотрены оригинальные программные средства, реализующие построение и анализ системы моделей струк-турной сложности и сходства, основанных на характеризации расположения фрагментов в топологии структур. Данные средства реализованы в виде подсистемы АСНИ «Graph Model Workshop» и нашли применение при исследовании отношений эквивалентности и толерантности на графовых моделях систем.
Abstract:We introduce the original software tools for building and analysis of the stratified system of structural complexity and similarity models. The models are based on the characterization of placement of fragments in a system topology. The software tools are implemented as a subsystem of the integrated research environment «Graph Model Workshop» and are used in studies of equality and tolerance relations of various graph models of systems.
| Авторы: Незнанов А.А. (aneznanov@hse.ru) - Государственный университет – Высшая школа экономики, г. Москва, кандидат технических наук, Кохов В.А. (viktorkokhov@rambler.ru) - Государственный университет – Высшая школа экономики, г. Москва, кандидат технических наук | |
| Ключевые слова: программный комплекс, структурное сходство, структурная сложность, графовая модель системы, структура |
|
| Keywords: software package, structural analysis, structural complexity, graph model of system, structure |
|
| Количество просмотров: 13430 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
Подход к построению и анализу моделей системы SGM Рассматриваемые программные средства используют принцип спектральной характеризации ГМС, дополненный учетом различных отношений между отдельными фрагментами, их классами или типами. ГМС t, изоморфно вкладываемая в исследуемую ГМС G, образует множество F(l)t помеченных фрагментов (ПФ) типа t. Каждый ПФ представляется каноническим изоморфным вложением t в G; g-модели самого верхнего уровня характеризуют расположение ПФ заданного набора типов T=(t1, …, tn) в топологии ГМС. Типы фрагментов, используемые при анализе ГМС, называют структурными дескрипторами (СД), а используемое множество СД – базисом СД. Подмодели SGM дополнительно характеризуют расположение классов эквивалентности ПФ (КЭПФ). Пределом разбиения КЭПФ служат орбиты t-группы, то есть группы, индуцированной группой автоморфизмов ГМС и действующей на ПФ типа t. Характеристики t-группы определяют симметрию расположения ПФ типа t в исследуемой ГМС.
Основные положения анализа сходства ГМС с использованием системы SGM Построение g-модели нетривиально (большинство задач, решаемых в процессе построения, принадлежат к классу NPC) и требует следующее: - определение базисов СД (Bl и Br) и, возможно, структурной сложности их элементов, если задано сохранение весов модели; - построение баз всех ПФ (F(l)ti) для всех СД, входящих в Bl и Br; - поиск орбит t-групп или КЭПФ для непустых F(l)ti, если задана свертка долей модели; - поиск общих частей ПФ (возможно, не всех ПФ для некоторых подмоделей); - вычисление коэффициентов сходства ПФ; - визуализация и/или сохранение модели. Приведем возможную последовательность этапов исследования сходства ГМС с использованием g-моделей (рис. 3). 1. Построение базы g-моделей заданного вида для базы исследуемых ГМС. 2. Формирование разнообразных отношений на g-моделях: - установление изоморфизма g-моделей; - установление изоморфного вложения g-моделей; - определение максимального общего фрагмента (МОФ) каждой пары g-моделей; - построение базы b(g)-моделей и определение МОФ b(g)-моделей – этот вариант более универсален и позволяет понизить вычислительную сложность с экспоненциальной (вариант с) до полиномиальной. 3. Экспорт полученных классов эквивалентности, кластеров толерантности или коэффициентов сходства в исходную базу или автоматическая генерация отчета. Границы применимости прямых методов анализа сходства моделей для ГМС общего вида: · для g-моделей – 45–100 вершин в зависимости от вида ГМС; · для b-моделей, построенных для g-модели (b(g)-моделей), – 250–400 вершин. Для отдельных классов графов граница применимости заметно повышается (до нескольких тысяч вершин для деревьев).
Полученные авторами результаты, связанные с обработкой t-групп, позволили реализовать эффективное построение gco(bco)-моделей, характеризующих расположение фрагментов с точностью до орбит t-групп. Программный комплекс FSS
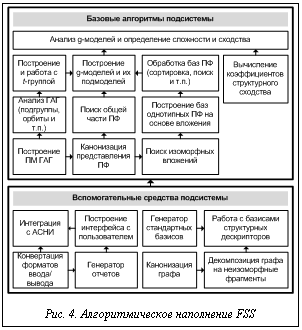
Основные особенности комплекса: - концепция автоматизированного проведения вычислительных экспериментов (все этапы выполняются с использованием FSS в пакетном режиме для баз ГМС, а результаты могут накапливаться в БД); - поддержка произвольных типов ГМС и их фрагментов, широкая параметризация моделей SGM, гибкая настройка используемых коэффициентов сходства ГМС; - ориентация на априори заданные базисы СД (декомпозиция ГМС используется именно для построения базисов); - единообразная обработка строковых и числовых весов вершин и ребер ГМС в любом количестве (что повышает качество исследования отношений эквивалентности и толерантности); - наличие исследовательских вариантов алгоритмов для сбора статистики и тонкого эмпирического анализа выполнения; - развитый графический интерфейс с пользователем на основе мастеров проведения экспериментов и системы работы с их результатами (включая развитый редактор отчетов с возможностью их накопления). В процессе реализации FSS выявлено и уточнено пространство параметризации SGM, признанное полезным для теоретических исследований и практического применения. Реализованная часть пространства параметризации g-моделей на текущий момент содержит 12 основных и 11 дополнительных параметров [2]. Основные параметры задают собственно математическую модель (число долей, вид свертки вершин при анализе расположения КЭПФ, отношения на ПФ и т.п.), а дополнительные определяют визуализацию (диапазон координат, расположение вершин, графические образы вершин, ребер и весов) и способ хранения модели. Модели могут сохраняться как непосредственно в виде взвешенного графа, так и в виде набора таблиц во встроенной БД результатов экспериментов. Из-за сложности параметризации в FSS применяется концепция работы с профилями. Профиль g-модели – совокупность используемых при ее построении атрибутированных базисов СД, параметров стратификации, параметров визуализации и сохранения моделей. Пользователю предлагаются несколько стандартных профилей и редактор профилей, включающий редактор базисов СД, причем среди базисов также выделены стандартные как наиболее популярные у исследователей. Рисунок 4 иллюстрирует алгоритмическую насыщенность комплекса. Использование новых методов учета симметрии расположения ПФ при реализации алгоритмов различения ГМС позволило на порядки поднять эффективность построения g-моделей для высокосимметричных ГМС. При этом основной упор сделан на исследование gco-моделей (со сверткой долей до орбит t-групп), так как модели без свертки долей становятся слишком большими для последующего эффективного анализа. Эксперименты показали, что gco(bco)-модели в среднем обеспечивают более адекватные результаты анализа сходства ГМС при акцентировании на различиях в топологии, а не на метрических характеристиках. На основе FSS впервые появилась возможность построения программных средств интеллектуального анализа структурных данных нового поколения. Исследуемые отношения эквивалентности и толерантности на основе системы моделей SGM заметно отличаются от большинства рассматриваемых в настоящее время и могут дополнять используемые методы анализа сходства ГМС [3]. Предлагаемые программные средства достигли достаточного уровня эффективности для широкого научного и практического применения. Примером практического применения может служить реализация нечеткого поиска (в том числе уточняемого) в базах структурной информации. Литература 1. Кохов В.А. Концептуальные и математические модели сложности графов. М.: Изд-во МЭИ, 2002. 2. Незнанов А.А., Кохов В.А. Программные средства для построения и исследования моделей структурной сложности и сходства // Одиннадцатая национ. конф. по искусствен. интел. с междунар. участ. КИИ-2008: тр. конф. М.: ЛЕНАНД, 2008. Т. 1. С. 216–224. 3. Cook D.J., Holder L.B. Mining Graph Data. Wiley-Interscience, 2006. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2624 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программная система для исследования вычислительной сложности решения задач на графовых моделях
- Аппаратно-программный комплекс для автоматизации контроля качества ферромагнитных материалов
- Риск-ориентированный подход к проектированию системы антитеррористической защищенности образовательных учреждений
- Программный комплекс для проектирования составов безобжиговых мономинеральных композитов
- Автоматизированное проектирование инструментов на основе моделирования технологии выдавливания металлов
Назад, к списку статей



 В настоящее время актуальной задачей является создание программных средств, позволяющих повысить эффективность исследования отношений эквивалентности и толерантности структур, что определяется потребностями анализа структурного сходства систем в различных областях (химическая информатика, распознавание образов, структурная лингвистика, интеллектуальный анализ данных). Наиболее общими подходами к анализу структурного сходства графовых моделей систем (ГМС) являются подструктурный (на основе поиска максимальных общих фрагментов ГМС) и структурно-характеристический (на основе сравнения различных видов моделей структурной сложности ГМС). Авторы активно участвуют в развитии оригинального обобщенного подструктурного подхода к анализу сходства, основанного на построении структурных инвариантов ГМС, позволяющих исследовать структурное сходство с учетом расположения и сходства расположения фрагментов в топологии ГМС. Стратифицированная иерархическая система моделей структурной сложности, предложенная в [1], получила название системы g-моделей (SGM). Одним из результатов реализации SGM стала подсистема «Fragments-Symmetry-Similarity» (FSS), расширяющая функциональное наполнение АСНИ «Graph Model Workshop».
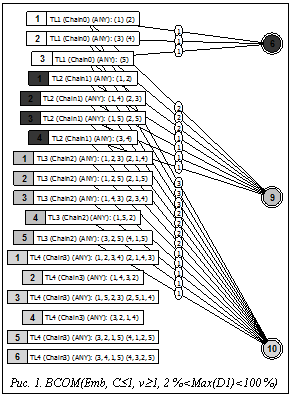
В настоящее время актуальной задачей является создание программных средств, позволяющих повысить эффективность исследования отношений эквивалентности и толерантности структур, что определяется потребностями анализа структурного сходства систем в различных областях (химическая информатика, распознавание образов, структурная лингвистика, интеллектуальный анализ данных). Наиболее общими подходами к анализу структурного сходства графовых моделей систем (ГМС) являются подструктурный (на основе поиска максимальных общих фрагментов ГМС) и структурно-характеристический (на основе сравнения различных видов моделей структурной сложности ГМС). Авторы активно участвуют в развитии оригинального обобщенного подструктурного подхода к анализу сходства, основанного на построении структурных инвариантов ГМС, позволяющих исследовать структурное сходство с учетом расположения и сходства расположения фрагментов в топологии ГМС. Стратифицированная иерархическая система моделей структурной сложности, предложенная в [1], получила название системы g-моделей (SGM). Одним из результатов реализации SGM стала подсистема «Fragments-Symmetry-Similarity» (FSS), расширяющая функциональное наполнение АСНИ «Graph Model Workshop».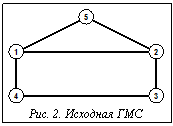 На основе предложенных моделей можно строить различные характеристические инварианты ГМС, как числовые, так и структурные. Построенные инварианты могут выражать метрические и спектральные свойства ГМС, симметрию расположения ПФ и разнообразие взаимного расположения ПФ разных типов в топологии ГМС. Наращивание базиса СД позволяет исследовать влияние расположения фрагментов различных типов на отношения эквивалентности и толерантности ГМС. При этом большинство подмоделей SGM являются двудольными графами и используют два базиса СД (левый и правый), которые могут различаться. Ребра моделей характеризуют отношения между ПФ (КЭПФ). В качестве отношений на помеченных фрагментах исследуемой ГМС рассматриваются отношения на основе операций пересечения и вложения ПФ. На рисунке 1 приведен пример визуализации bco-модели, отражающей отношения между орбитами ПФ (цепей длины 0–3) и типами ПФ (цепей длины 1–3) для ГМС, изображенной на рисунке 2.
На основе предложенных моделей можно строить различные характеристические инварианты ГМС, как числовые, так и структурные. Построенные инварианты могут выражать метрические и спектральные свойства ГМС, симметрию расположения ПФ и разнообразие взаимного расположения ПФ разных типов в топологии ГМС. Наращивание базиса СД позволяет исследовать влияние расположения фрагментов различных типов на отношения эквивалентности и толерантности ГМС. При этом большинство подмоделей SGM являются двудольными графами и используют два базиса СД (левый и правый), которые могут различаться. Ребра моделей характеризуют отношения между ПФ (КЭПФ). В качестве отношений на помеченных фрагментах исследуемой ГМС рассматриваются отношения на основе операций пересечения и вложения ПФ. На рисунке 1 приведен пример визуализации bco-модели, отражающей отношения между орбитами ПФ (цепей длины 0–3) и типами ПФ (цепей длины 1–3) для ГМС, изображенной на рисунке 2.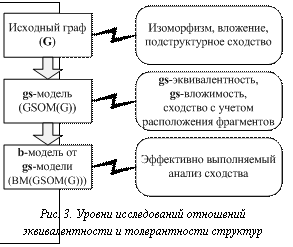
 Комплекс FSS предназначен для автоматизации исследования широкого класса отношений эквивалентности и толерантности ГМС, строящихся на основе различных классов моделей системы SGM. Комплекс реализован в виде набора расширений АСНИ «Graph Model Workshop» и образует замкнутую подсистему, которая, однако, хорошо интегрирована с другими подсистемами АСНИ. Разработка была начата в 2003 году, сейчас доступна вторая версия FSS. Комплекс создан с использованием сред CodeGear RAD Studio (язык Delphi) и Microsoft Visual Studio (C++). Объем авторского исходного кода – более 2 Мб, число компилируемых строк исходного кода – более 620 000, объем машинного кода – 6,2 Мб. АСНИ «Graph Model Workshop» работает под управлением ОС Microsoft Windows 98-Vista.
Комплекс FSS предназначен для автоматизации исследования широкого класса отношений эквивалентности и толерантности ГМС, строящихся на основе различных классов моделей системы SGM. Комплекс реализован в виде набора расширений АСНИ «Graph Model Workshop» и образует замкнутую подсистему, которая, однако, хорошо интегрирована с другими подсистемами АСНИ. Разработка была начата в 2003 году, сейчас доступна вторая версия FSS. Комплекс создан с использованием сред CodeGear RAD Studio (язык Delphi) и Microsoft Visual Studio (C++). Объем авторского исходного кода – более 2 Мб, число компилируемых строк исходного кода – более 620 000, объем машинного кода – 6,2 Мб. АСНИ «Graph Model Workshop» работает под управлением ОС Microsoft Windows 98-Vista.