Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Поиск регулярных решеток на текстуре фасадов зданий
Аннотация:В статье описан алгоритм поиска набора непересекающихся решеток похожих прямоугольных частей ректифи-цированного изображения фасада городского здания. Нахождение прямоугольников и запоминание частых расстояний между ними позволяют уменьшить число возможных решеток. Лучшие решетки выбираются итерационно с учетом эмпирических наблюдений о похожести и симметричности ячеек. Сравнение с двумя современными алгоритмами показало превосходство предложенного алгоритма.
Abstract:We present a novel algorithm for automatic extraction of a set of non-overlapping grids of similar facade parts from single rectified image. The most frequent possible grid cells sizes and grid cells centers are estimated by detecting and analyzing similar rectangles in input image. Greedy iterative algorithm sequentially chooses grids with maximum quality measure that incorporates empirical observations about similarities and symmetries. Comparison hows that the proposed algorithm outperforms two other state-of-the-art methods and can handle occlusions.
| Авторы: Якубенко А.А. (toh@graphics.cs.msu.ru) - Московский государственный университет имени М.В. Ломоносова, Мизин И.С. (vamizi@front.ru) - Московский государственный университет имени М.В. Ломоносова, Конушин А.С. (ktosh@graphics.cs.msu.ru) - Московский государственный университет им. М.В. Ломоносова, Ленинские горы, 1-52, г. Москва, 119991, Россия; Национальный исследовательский университет «Высшая школа экономики», ул. Мясницкая, 20, г. Москва, 101000, Россия (доцент), Москва, Россия, кандидат физико-математических наук | |
| Ключевые слова: распознавание, фасад, структура, регулярность, решетка, городской, трехмерная карта, текстура, окклюзии, компьютерное зрение |
|
| Keywords: identification, facade, structure, regularity, grid, urban, 3D city map, texture, occlusion, computer vision |
|
| Количество просмотров: 15437 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
Эффективное создание трехмерных карт городов является одной из актуальных задач на сты- ке геоинформатики и компьютерного зрения. Трехмерные карты – это естественная эволюция привычных плоских карт. Такие карты можно использовать как для решения традиционных задач навигации, городского планирования и тому подобных, так и для открытия новых возможностей сервисам виртуальной и расширенной реальности. Основным содержимым трехмерных карт являются трехмерные модели городских зданий. Существует несколько способов их получения. Они могут быть созданы, например, из разрозненных фотографий автоматически или вручную с помощью фотограмметрического ПО или трехмерных редакторов. Для редактирования текстур обычно используется Adobe Photoshop или другое подобное ПО. Более автоматизированные подходы предполагают обработку облаков трехмерных точек и видеопотока с систем мобильной съемки. Также могут использоваться данные аэрофотосъемки и воздушного лазерного сканирования. Трехмерную модель городского здания можно условно разделить на две части: фасад и крыша. Крыши могут быть смоделированы по аэрофото или данным с воздушных лидаров с помощью ручных инструментов либо путем автоматической подгонки параметрических моделей крыш под имеющиеся данные. Моделирование фасадов – более трудная задача. Но здания обычно обладают структурой и регулярностью. Эти семантические знания могут помочь в решении многих проблем в моделировании, обработке и интерпретации фасадов. Текстуры фасадов зачастую загорожены объектами переднего плана (растительность, рекламные вывески, провода, автомобили, люди, другие здания, выпуклые части зданий). Загороженные области (окклюзии) могут быть сегментированы и восстановлены путем сравнения повторяющихся частей фасада [1, 2]. Текстуры, полученные с аэрофото, часто имеют низкое разрешение и плохое качество при приближении к нижним этажам зданий. Если извлечь информацию о разбиении фасада на этажи, тогда можно перенести текстурную информацию с верхних этажей на нижние [3]. Обнаруженные фасадные элементы, такие как окна или балконы, могут быть заменены более детализированными шаблонными трехмерными моделями для повышения общего качества восприятия. Знания о повторяющихся участках текстуры и соответствующих элементах геометрии могут использоваться для сжатия файлов трехмерной модели и текстуры, что важно для интернет-приложений, информация о структуре фасадов зданий – для сервисов геолокации и других задач. Существующие методы Повторяемость и регулярность – главные подсказки при интерпретации фасадов. Классическим решением для извлечения регулярности из изображения плоского объекта без перспективных искажений является анализ пиков автокорреляции изображения, когда глобально анализируется все изображение. Но это подходит только для случаев одной строгой регулярности, которая занимает большую часть изображения без значительных окклюзий.
Упомянутые подходы не фокусируются исключительно на фасадах. Целью другой группы методов является поиск окон, которые чаще всего определяют структуру здания. Это может быть сделано с помощью детектора, подобного Viola-Jones, с использованием признаков Хаара и метода главных компонент или усиления слабых классификаторов. Окна сильно отличаются друг от друга, поэтому такие подходы хорошо работают только в пределах базы с довольно похожими изображениями. Для решения данной проблемы предлагался подход с последовательным обучением, но он требовал взаимодействия с пользователем. Эвристические подходы используют похожесть углов окон и наличие градиента по периметру окон. Для регуляризации используется критерий Акаике или принцип минимальной длины описания [5]. Поиск окон также может быть сформулирован в виде задачи оптимальной разметки изображения или в виде задачи поиска оптимального набора непересекающихся прямоугольников. Текущие результаты алгоритмов поиска окон не дают возможности использовать их как финальное решение. Но найденные окна могут быть востребованы как низкоуровневая информация для более интеллектуальных алгоритмов, которые будут учитывать и регулярность. Результаты семантической сегментации изображений в общей постановке и сегментации области стен также далеки от желаемых. Лучшие алгоритмы для интерпретации фа- садов пытаются описать входное изображение фасада высокоуровневой моделью. Эта модель может быть представлена как разбиение фасада на этажи, пролеты, окна и т.д. В более общем случае она может описывать грамматический вывод [3]. Выбор правил грамматики (например, для вертикальных или горизонтальных разделений) и их параметров (например, координат разделений) может осуществляться с помощью случайных марковских цепей с использованием в качестве метрики взаимной информации или края внутри и между фрагментами-кандидатами [3]. Метрическая информация позволяет уменьшить пространство параметров. Это один из наиболее перспективных подходов, но текущие результаты с трудом справляются с окклюзиями и сильно зависят от правил грамматического вывода и выбора метрик. Предлагаемый метод На вход принимается ректифицированное изображение фасада. В предположении, что фасад плоский, ректифицированное изображение компенсирует проективные искажения. Такое изображение может быть получено непосредственно из текстуры уже созданной трехмерной модели или из входной фотографии (рис. 1). Последнее может быть сделано либо путем указания четырех точек, задающих прямоугольник в трехмерном пространстве, либо с помощью автоматических алгоритмов, которые находят линии на изображении и группируют их в соответствии с точками схо- да (рис. 2). Целью авторов была разработка алгоритма, способного работать на изображениях разнообразных фасадов, частично перекрытых посторонними предметами. Поэтому не следовало использовать слишком жесткую модель. Был выбран набор непересекающихся решеток похожих между собой прямоугольных фрагментов в качестве простой и гибкой модели, которая описывает большинство городских зданий.
Схема предложенного алгоритма изображена на рисунке 3: сначала на изображении находятся прямоугольники, затем выбираются самые частые расстояния между потенциальными ячейками решеток Поиск прямоугольников. Для поиска прямоугольников со сторонами, параллельными осям изображения, может использоваться преобразование Хафа. Но авторы предлагают другой алгоритм, обеспечивающий более высокое качество. Строится пирамида изображений путем уменьшения изображения в 2 и 4 раза. С помощью оператора Собеля отдельно выделяются вертикальные и горизонтальные границы. Пиксель на исходном изображении помечается как край, если в данном пикселе есть край на всех уровнях пирамиды. Такой подход позволяет отфильтровать маленькие и шумные края, например, между кирпичами. Если у пикселя достаточно вертикальных краев снизу и горизонтальных краев справа, он помечается как кандидат в верхний левый угол прямоугольника. Аналогично осуществляется поиск кандидатов других типов углов прямоугольника. Перебираем все пары углов. Если пара углов может сформировать прямоугольник, то есть углы лежат на одной вертикальной или горизонтальной прямой и имеют соответствующие типы (например, верхний левый и нижний левый), расстояние между ними сохраняется. Далее проводится жадный поиск прямоугольников с найденными углами и отобранными расстояниями (рис. 4). В примере на иллюстрациях находится около 10 000 углов и 1 000 таких прямоугольников.
Вычисление кандидатов размеров и центров ячеек решеток. Сравниваем каждую пару фрагментов изображения, соответствующих прямоугольникам одинакового размера, с помощью нормализованной кросс-корреляции и сохраняем расстояния, если значение метрики достаточно велико. Самые частые расстояния становятся кандидатами размеров ячеек решеток (рис. 4). Решетки выглядят естественно, если в центре их ячеек находится какой-то фасадный элемент, например окно. Такое центрирование решеток необязательно, но оно позволяет снизить число возможных решеток и предотвращает потерю отдельных рядов и столбцов ячеек вблизи краев изображения. Жадный выбор лучших решеток. Число потенциальных решеток достаточно мало для осуществления полного перебора. Качество решетки
где
где Последовательно выбираем лучшую решетку, которая не пересекает уже найденные решетки (рис. 5); останавливаемся, когда качество вновь найденной решетки существенно ниже самой лучшей решетки. Поиск дополнительных решеток. Некоторые решетки могут быть пропущены на предыдущем этапе анализа, поэтому проводится поиск дополнительных решеток (рис. 6). Предположим, что пропущенные решетки имеют ячейки, похожие на уже найденные. Вычисляем медианное изображение ячейки для каждой решетки и коррелируем его с частью изображения, еще не покрытой решетками. Если пик корреляции достаточно велик, ищем новую решетку с центром в найденном пике. Алгоритм поиска дополнительных решеток итерационно запускается, пока находятся новые решетки. Расширение решеток. Найденные решетки обычно не заходят в области окклюзий. Для каждой решетки рассматриваем четыре решетки, получаемые из исходной добавлением к ней одной строки или одного столбца. Если данная решетка не пересекает другие решетки и новые ячейки похожи на соседние (с меньшим порогом), исходная решетка заменяется расширенной (рис. 6, 7). Данный алгоритм применяется несколько раз: сначала после нахождения лучших решеток для объединения частично загороженных ячеек перед поиском дополнительных решеток, затем после нахождения дополнительных решеток. Наконец, он применяется с очень низким порогом на сходство ячеек к финальным решеткам для их продолжения в области сильных окклюзий. Эксперименты и сравнение База изображений. Не существует признанной метрологии или хотя бы базы изображений для тестирования и сравнения алгоритмов интерпретации фасадов зданий. Авторы выбрали 25 изображений из Facade Data Base Vienna, eTRIMS Image Database, ZuBuD Image Database, портала CGTextures.com и своих собственных фотографий. Это небольшая, но репрезентативная база, включающая изображения зданий старинной и современной архитектуры, построенных из различных материалов, с разным числом этажей и пролетов, разными типами регулярности, снятые в разных условиях. Все изображения были вручную ректифицированы.
Алгоритм в работе [5] – тренд использования более сложных моделей для описания фасадов. Модель представляет собой линейную комбинацию сдвигов вдоль осей изображения с соответ- ствующими коэффициентами, а также регуляризацию согласно принципу минимальной длины описания. Алгоритм находит SIFT-особенности и выделяет среди них пары похожих. Подбираются такие параметры модели, чтобы похожие особенности переходили друг в друга. Оценка нахождения размеров ячеек решеток. Алгоритмы, выбранные для сравнения, не пытаются центрировать решетки по окнам, поэтому они могут терять некоторые строки и столбцы ячеек. Предложенный алгоритм находит правильные размеры ячеек решеток в числе 10 самых частых размеров на всех изображениях базы. Но некоторые из правильных решеток пропущены в финальном результате. По мнению авторов, размер ячеек решеток был определен правильно, если в финальном результате есть решетка с верным размером ячеек. Согласно данному критерию предложенный алгоритм верно определяет размеры ячеек решеток на 88 % тестовых изображений, алгоритм из работы [4] – на 68 %, алгоритм из [5] – на 56 %. Оценка доли верно найденных похожих элементов. Авторы считают, что найденная решетка определена верно, если все ее ячейки визуально похожи, более не подлежат дроблению и имеют верное число строк и столбцов. Локальные сдвиги решеток не принимаются во внимание, так как это некритично для последующей обработки найденных решеток, например, для восстановления текстуры в области окклюзий. Но данные сдвиги могут влиять на число строк и столбцов решетки. Правильные размеры решеток известны благодаря ручной разметке базы изображений. Для оценки вычисляем отношение числа верно найденных ячеек к должному общему числу ячеек. Результаты показаны на рисунке 8. Сравнение не проводится с алгоритмом из работы [5], так как для позиционирования решетки он требует указания ее начала вручную.
В первую очередь, это может быть объяснено тем, что предложенный алгоритм рассчитан на работу исключительно с ректифицированными изображениями, а не с исходными фотографиями. Также алгоритм ориентируется на работу только с ограниченным классом регулярностей, часто встречающихся на фасадах городских зданий. В отличие от сложных грамматических моделей авторы предложили простую модель – набор непересекающихся решеток, – которая описывает абсолютное большинство фасадов. В предложенную меру качества решеток входят эмпирические знания о фасадах зданий, включая похожесть соседних ячеек, горизонтальную симметричность ячеек и наличие прямоугольника в центре ячейки. Для анализа использовались прямоугольники, часто встречающиеся на изображениях фасадов и оказавшиеся более надежными, чем точечные особенности или случайные фрагменты. Было уменьшено возможное число размеров ячеек решеток путем сбора наиболее часто встречающихся расстояний между найденными прямоугольниками. Центры прямоугольников являются кандидатами на сдвиги решеток. Благодаря такому уменьшению числа возможных решеток становится возможным их полный перебор для итерационного выбора лучших решеток. Предложенный алгоритм справляется с окклюзиями с помощью понижения порогов на качество решеток при их расширении. Несмотря на то, что результаты предложенного алгоритма довольно обнадеживающие, алгоритм имеет ряд недостатков. Из-за алгоритма жадного выбора лучших решеток некоторые из них пропускаются и не все окклюзии обрабатываются. Также одна решетка, разделенная другой, представляется в виде двух решеток. Постановка задачи в виде задачи глобальной оптимизации могла бы дать лучшие результаты. Поиск прямоугольников довольно прост и надежен, но дополнительный поиск окон с помощью детектора, основанного на машинном обучении, мог бы улучшить общий результат. По предположению авторов, фасадные элементы плоские, но выпуклые балконы и глубоко вдавленные окна требуют трехмерного анализа. Представления фасада в виде набора непересекающихся решеток одинаковых ячеек достаточно для задач восстановления текстуры и сжатия модели. Но предложенная модель может быть улучшена за счет введения иерархии и более сложных моделей повторения, например, повторяющихся пар элементов. Литература 1. Korah T., Rasmussen C. Analysis of Building Textures for Reconstructing Partially Occluded Facades, ECCV. 2008. Part 1, pp. 359–372. 2. Konushin V., Vezhnevets V. Automatic building texture completion, Proc. of GraphiCon’2007. M.: MSU, 2007. Vol. 1, pp. 174–177. 3. Muller P., Zeng G., Wonka P. and L. Gool V. Image-based Procedural Modeling of Facades, SIGGRAPH. 2007. Vol. 26, No. 3, pp. 1–9. 4. Minwoo Park, Robert T. Collins and Yanxi Liu. Deformed Lattice Discovery Via Efficient Mean-Shift Belief Propagation, ECCV. 2008. Vol. 2, pp. 474–485. 5. Wenzel S., Drauschke M., Forstner W. Detection of Repeated Structures in Facade Images // Pattern Recognition and Image Analysis. 2008. Vol. 18, No. 3, pp. 406–411. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2641 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Семантическая сегментация данных лазерного сканирования
- Использование энтропийных мер в задачах оценки информативности признаков распознавания образов
- Разработка информационной системы расчета, накопления информации и паспортизации теплофизических свойств фосфоритов
- Подсчет количества людей в видеопоследовательности на основе детектора головы человека
- Разработка алгоритма направленного распознавания с учетом информации о рельефе на примере спутниковых снимков и данных дистанционного зондирования Земли
Назад, к списку статей



 Для работы с околорегулярными текстурами, перспективными искажениями, частичными ок- клюзиями можно использовать разреженные фрагменты изображения. Они могут выбираться случайным образом либо как окрестности особых точек [4] или прямоугольников [1]. Похожие фрагменты группируются исходя из модели гомографии, решетки [1], околорегулярной решетки [4] или более сложной модели [5]. Фрагменты сравниваются друг с другом либо с помощью метрик вроде попиксельной суммы квадратов разностей цветов или нормализованной кросс-корреляции, либо с помощью сравнения дескрипторов, например SIFT. В зависимости от сложности модели она может оцениваться с помощью преобразования Хафа, алгоритмов семейства RANSAC, итерационного распространения решеток [4] или оптимизации марковского поля [1]. Эти подходы показали хорошие результаты на многообразии изображений. Из-за обобщенной постановки задачи и использования только небольших локальных фрагментов изображения качество работы таких алгоритмов резко падает при анализе более сложных фасадов, например, несовременных зданий, фасадов с несколькими решетками, значительными областями перекрытия.
Для работы с околорегулярными текстурами, перспективными искажениями, частичными ок- клюзиями можно использовать разреженные фрагменты изображения. Они могут выбираться случайным образом либо как окрестности особых точек [4] или прямоугольников [1]. Похожие фрагменты группируются исходя из модели гомографии, решетки [1], околорегулярной решетки [4] или более сложной модели [5]. Фрагменты сравниваются друг с другом либо с помощью метрик вроде попиксельной суммы квадратов разностей цветов или нормализованной кросс-корреляции, либо с помощью сравнения дескрипторов, например SIFT. В зависимости от сложности модели она может оцениваться с помощью преобразования Хафа, алгоритмов семейства RANSAC, итерационного распространения решеток [4] или оптимизации марковского поля [1]. Эти подходы показали хорошие результаты на многообразии изображений. Из-за обобщенной постановки задачи и использования только небольших локальных фрагментов изображения качество работы таких алгоритмов резко падает при анализе более сложных фасадов, например, несовременных зданий, фасадов с несколькими решетками, значительными областями перекрытия.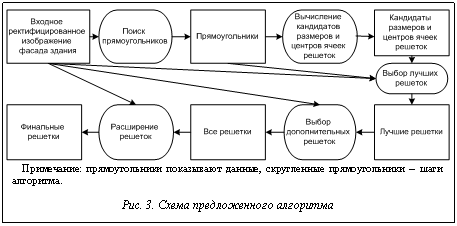 Оси решетки параллельны осям изображения. Каждая решетка описывается шестью параметрами:
Оси решетки параллельны осям изображения. Каждая решетка описывается шестью параметрами:  –
–  - и -координаты верхнего левого угла решетки,
- и -координаты верхнего левого угла решетки, 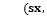 – размер ячейки решетки,
– размер ячейки решетки, 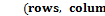 – число рядов и столбцов в решетке.
– число рядов и столбцов в решетке.

 оценивается следующим образом:
оценивается следующим образом: ,
, – число рядов решетки;
– число рядов решетки;  =-0,8 – регуляризующий параметр, штрафующий слишком маленькие решетки;
=-0,8 – регуляризующий параметр, штрафующий слишком маленькие решетки;  – значение меры качества ячейки
– значение меры качества ячейки  :
:
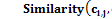 – значение меры сходства между ячейками
– значение меры сходства между ячейками 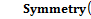 – значение меры горизонтальной симметрии ячейки
– значение меры горизонтальной симметрии ячейки 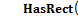 равно
равно 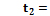 . Пороги
. Пороги  Алгоритмы для сравнения. Постановка задачи интерпретации фасадов у многих авторов отличается, поэтому выбран алгоритм из [4] как наиболее предпочтительный для восстановления регулярностей общего вида. Он основан на поиске особых точек и сравнении их окрестностей. Алгоритм запоминает сдвиги между похожими точками. Часто повторяющиеся сдвиги становятся гипотезами для размеров начальной гибкой решетки. Решетки строятся итеративно путем добавления новых ячеек, похожих на ранее найденные и удовлетворяющих ограничениям на размеры ячеек. Некоторые части авторского алгоритма основываются на идеях, предложенных в [4].
Алгоритмы для сравнения. Постановка задачи интерпретации фасадов у многих авторов отличается, поэтому выбран алгоритм из [4] как наиболее предпочтительный для восстановления регулярностей общего вида. Он основан на поиске особых точек и сравнении их окрестностей. Алгоритм запоминает сдвиги между похожими точками. Часто повторяющиеся сдвиги становятся гипотезами для размеров начальной гибкой решетки. Решетки строятся итеративно путем добавления новых ячеек, похожих на ранее найденные и удовлетворяющих ограничениям на размеры ячеек. Некоторые части авторского алгоритма основываются на идеях, предложенных в [4].![Подпись:
а б
Рис. 8. Оценка доли верно найденных ячеек:
а) для предложенного алгоритма, б) для алгоритма из [4]](uploaded/image/2010-4/image1229.gif) Подводя итог, можно отметить, что авторами предложен новый, полностью автоматический алгоритм для извлечения информации о регулярно повторяющихся прямоугольных фрагментах ректифицированного изображения фасадов городских зданий. Проведенное сравнение показало превосходство предложенного метода.
Подводя итог, можно отметить, что авторами предложен новый, полностью автоматический алгоритм для извлечения информации о регулярно повторяющихся прямоугольных фрагментах ректифицированного изображения фасадов городских зданий. Проведенное сравнение показало превосходство предложенного метода.