Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Методика расчета коэффициентов сравнительной ценности диагностических показателей
Аннотация:Описывается методика расчета коэффициентов сравнительной ценности частных диагностических показателей, основанная на модифицированной процедуре парных сравнений их значимости и задаваемом экспертом отношении частичной транзитивности парных оценок для использования этих коэффициентов при проведении комплексной оценки психического и физиологического состояния обследуемых в фиксированный момент и во временной динамике с помощью предложенных ранее интегральных диагностических показателей и их систем.
Abstract:The procedure of calculation of the coefficients of the comparative value of particular diagnostic indices, based on the modified procedure of the paired comparisons of their significance and the relation of the partial transitivity of the paired estimations given by expert is described. These coefficients are used with conducting of the integrated assessment of the mental and physiological state of men investigated at the fixed moment of time and in the temporary dynamics with the aid of integral diagnostic indices and their systems proposed earlier.
| Авторы: Ермаков А.Е. (alerma@rambler.ru) - Военно-медицинская академия им. С.М. Кирова, г. Санкт-Петербург, г. Санкт-Петербург, Россия, кандидат технических наук | |
| Ключевые слова: автоматизированная система, отношение частичной транзитивности парных (бинарных) оценок, метод парных сравнений, парное сравнение ценности частных показателей, частный диагностический показатель, психологическая (физиологическая) характеристика |
|
| Keywords: an automated system issue, relation of the partial tranistivity of the paired (binary) estimations, method of paired comparisons, paired comparison of the value of particular indices, particular diagnostic index, : psychological (physiological) characteristic |
|
| Количество просмотров: 13518 |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
Методика комплексной сравнительной оценки психического и физиологического состояния (ПФС) обследуемых, основанная на применении отдельных интегральных диагностических показателей (ИДП) и их систем, а также специальных процедур вычисления значений ИДП, одной из которых является процедура расчета коэффици- ентов сравнительной ценности частных диагностических показателей (ЧДП), описана в [1, 2]. Сравнительная оценка ПФС обследуемых может проводиться при наличии априорно заданных экспертных требований к значениям ЧДП, разделяющих множества их значений на два или более непересекающихся подмножеств и при отсутствии каких-либо априорных требований к значени- ям ЧДП. В ходе обследования респонденты сравниваются по заранее отобранному специалистами набору психологических, физиологических и психофизиологических характеристик (ПФХ). Каждая ПФХ оценивается посредством одного или нескольких ЧДП. В результате каждому респонденту сопоставляется множество значений ЧДП, оценивающих его ПФХ. В контексте диагностической задачи все рассматриваемые ПФХ имеют определенную ценность, которую эксперт способен сопоставить в ходе их парного сравнения. Ситуация парной несравнимости ПФХ и ЧДП по ценности считается недопустимой. В теории принятия решений доказано, что попарное сравнение ценности ЧДП более объективно и достоверно, чем прямое экспертное присвоение ЧДП коэффициентов ценности и множественное единовременное сравнение значимости ЧДП. Сравнительная ценность ПФХ и ЧДП описывается через коэффициенты, вычисляемые на основе частной методики, имеющей отличия от аналогов, описанных в том числе и в [3–5]. На первом этапе методики сравнения ПФС обследуемых эксперт задает качественную измерительную шкалу для парного сравнения ценности ЧДП, для которой затем директивно или алго- ритмически формируется рациональный вариант сопряженной с ней числовой шкалы. Далее у эксперта выясняются и алгоритмически формируются качественные оценки сравнительной значимости пар ЧДП и на основе их числовых аналогов вычисляются коэффициенты ценности ЧДП, количественно описывающие сравнительную значимость соответствующих ПФХ в контексте диагностической задачи. На втором этапе выполняется собственно расчет значений ИДП для каждого из обследуемых на основе измеренных у них значений ЧДП, коэффициент сравнительной ценности этих ЧДП, а для части описанных в [1, 2] систем ИДП – априорных требований к значениям ЧДП. На третьем этапе производятся сравнение полученных значений ИДП и ранжирование обследуемых. По мнению автора статьи, корректная и удобная процедура сравнения ценности альтернатив должна обладать следующими свойствами. 1. Обеспечивать высокую точность и безошибочность выполняемых расчетов, а также формирование внутренне непротиворечивых систем оценок, что достигается: - использованием корректных допущений и предположений об особенностях исследуемых объектов и возможностях их исследователей – ЧДП, бинарных оценках их сравнительной значимости, измерительных шкалах бинарных оценок, экспертах; - использованием измерительных шкал, адекватных решаемой задаче, выразительным возможностям языка и измерительным возможностям эксперта; - применением обоснованных и адекватных математических и эвристических методов обработки экспертных оценок и превращения их в коэффициенты сравнительной ценности альтернатив; - использованием алгоритмических средств выявления и предотвращения возможных противоречий в экспертных оценках; - применением алгоритмических процедур, обеспечивающих автоматическое формирование бинарных оценок, согласованных с ранее найденными оценками. 2. Обеспечивать хорошую верифицируемость и интерпретируемость полученных результатов силами использующих ее специалистов, что достигается: - применением измерительных шкал, обладающих ясным для эксперта физическим смыслом и соответствующих его измерительным возможностям; - использованием процедур расчета значений коэффициентов сравнительной ценности, содержательно понятных применяющим их специалистам и пригодных для проверки ими. 3. Минимизировать вопросную нагрузку на эксперта, требуемую для нахождения весов ЧДП, и обладать низкой вычислительной сложностью. Описываемая в работе методика расчета значений коэффициентов сравнительной ценности ЧДП в определенной степени обладает перечисленными свойствами и отличается от аналогов. Рассмотрим подробнее предлагаемую методику и процедуру расчета коэффициентов сравнительной ценности {wx³0, x=1, ..., n} ЧДП {px} на основе парных оценок их сравнительной значимости. Результат парного сравнения ценности ЧДП является мерой доминирования по ценности одного из них над другим. Интенсивность доминирования одного ЧДП над другим оценивается значениями пар адекватных решаемой задаче качественных и числовых измерительных шкал. Коэффициент wx ЧДП px трактуется как суммарная мера доминирования по ценности ЧДП px себя и остальных ЧДП задачи. Из [3] известно, что при парном сравнении ценности нескольких альтернатив (объектов) нередко используются трехзначные качественные шкалы со значениями {«менее ценен», «равны по ценности», «более ценен»} и их числовые эквиваленты – {0; 0,5; 1}, {0; 1; 1}, а также сопряженные пары 11–18-значных шкал, первые из которых дают слишком грубую оценку соотношения ценности ЧДП в парах, а вторые требуют от экспертов экстраординарных измерительных способностей – умения надежно различать превосходство умеренное, существенное, значительное и очень сильное [4]. В [1, 2] для парного сравнения ценности ЧДП предложено использовать две сопряженные измерительные шкалы – качественную, содержащую удобные для эксперта качественные формулировки соотношения ценности пар ЧДП, и числовую, количественно характеризующую это соотношение. В роли наиболее удобной для многих экспертов автором использовалась семизначная качественная шкала со значениями: ЗБЦ (значительно более ценен), БЦ (более ценен), НБЦ (немного более ценен), РЦ (равны по ценности), НМЦ (немного менее ценен), МЦ (менее ценен), ЗМЦ (значительно менее ценен). Более тонкие градации взаимных отличий ценности пар ЧДП редко используются медиками, психологами и физиологами, а более грубые могут внести в формируемые коэффициенты ценности ЧДП неконтролируемые погрешности, однако излагаемые далее результаты справедливы и для шкал с другим нечетным числом значений. Использование такой качественной шкалы эквивалентно заданию на множестве пар ЧДП {(px, py), x=1,...,n, y=1,...,n} отношения Rк(px, py)® ®mкzÎMкзн с множеством значений Mкзн={ЗБЦ, БЦ, НБЦ, РЦ, НМЦ, МЦ, ЗМЦ}. Здесь mкz – z-й элемент Мкзн; ® – символ отображения. Рассматриваемая качественная шкала содержательно симметрична относительно центрального значения РЦ, а значения в парах (ЗБЦ, ЗМЦ), (БЦ, МЦ), (НБЦ, НМЦ) содержательно равноудалены от значения РЦ. Несложно показать, что Rк(px, py) в этом случае имеет свойства: 1) для любых пар ЧДП {(px, py), x≠y} справедливы соотношения: Rк(px, py)=ЗМЦÞRк(py, px)=ЗБЦ, Rк(px, py)=ЗБЦÞRк(py, px)=ЗМЦ, Rк(px, py)=МЦÞRк(py, px)=БЦ, Rк(px, py)=БЦÞRк(py, px)=МЦ, (1) Rк(px, py)=НМЦÞRк(py, px)=НБЦ, Rк(px, py)=НБЦÞRк(py, px)=НМЦ, Rк(px, py)=РЦÞRк(py, px)=РЦ. 2) " px справедливо: Rк(px, px)=РЦ. Эти свойства Rк(px, py) и порождаемой им качественной шкалы использовались автором при прямом задании и алгоритмическом формировании сопряженной с ней числовой шкалы, значения которой характеризуют количественную меру доминирования по ценности одного ЧДП над другим, а также для задания числового отношения Rч(px, py)®mчzÎMчзн, сопряженного с Rк(px, py). Через Мчзн и mчz обозначены множества всех значений Rч(px, py) и его z-й элемент. Множеством значений числовых оценок сравнительной значимости пар альтернатив традиционно считается {0; 1} [3, 5] или [0; mчmax], где mчmax>1 [4]. В данной работе расширено множество возможных числовых эквивалентов значений качественной шкалы, которые в [1, 2] использовались для количественной парной оценки сравнительной ценности ЧДП. В [1] рассматривалось несколько вариантов сопряженных числовых шкал, в том числе шкалы {0; 0,167; 0,334; 0,501; 0,668; 0,835; 1,002} и {0; 0,166; 0,332; 0,498; 0,664; 0,83; 0,996}. Коэффициенты ценности ЧДП {wi, i=1, …, n}, сформированные на основе парного сравнения их значимости с помощью числовых шкал, принимают значения в диапазоне [0,5×mчmax; (n–1)× ×mчmax+0,5×mчmax], то есть [0,5×mчmax; (n–0,5)× ×mчmax] ([0,501; (n–0,5)×1,002] и [0,498; (n–0,5)× ×0,996] для ранее приведенных шкал), для удобства разделив границы которого на (n–0,5)×mчmax (нормировав), а затем умножив числитель и знаменатель дроби на 2, получим: " wiÎ Числовой аналог качественной оценки РЦ и коэффициент сравнительной ценности наименее ценного ЧДП px при этом будут равны Если остальные значения Rк располагаются попарно симметрично вокруг значения РЦ, то для соответствующих им пар значений Rч будет справедливо соотношение: " (pi, pj), i¹j: Rч(pi, pj)=mÞRч(pj, pi)=
Из теории измерений [5] известно, что прямой переход от более слабых качественных, обычно порядковых, шкал к более сильным числовым шкалам в общем случае неправомерен и не приветствуется. В то же время такой переход в принципе возможен и успешно используется при решении прикладных задач, например, в методе анализа иерархий [4]. Обоснованный переход от качественных шкал к числовым шкалам отношений в ходе измерения интенсивности превосходства одного ЧДП над другим при их парном сравнении становится возможным в рамках предлагаемой трактовки этих качественных шкал как более мощных, чем порядковые, и благодаря привлечению дополнительных экспертных знаний об исследуемых объектах – эвристик и предположений, уточняющих соотношения между значениями шкал. Эксперт в зависимости от специфики решаемой задачи и своих представлений может считать задаваемую качественную шкалу содержательно равномерной, и тогда ее значения будут содержательно равноудалены друг от друга, или неравномерной. Для равномерной семизначной качественной шкалы полагаем, что сопряженная с ней числовая шкала также будет равномерной, а числовые аналоги {mi, i=1, …, nоц} качественных значений находятся по формуле ЗМЦ~0, МЦ НМЦ РЦ НБЦ БЦ ЗБЦ Здесь и далее «~» означает соответствие значений двух заданных экспертом сопряженных измерительных шкал (качественной и числовой). Для неравномерной семизначной качественной шкалы числовые аналоги ее значений также могут быть найдены на основе определенных экспертных предположений, например о том, что ЗМЦ~0, ЗБЦ~ ЗМЦ~0, МЦ~ НМЦ РЦ НБЦ БЦ ЗБЦ Если числовой аналог какого-либо значения качественной шкалы – периодическое число или имеет слишком много знаков после запятой, то оно округляется до 3–5 знаков после запятой, а значение z корректируется для сохранения истинности используемых эвристик (2), (3), например, 0,01(3) меняется на 0,0133. Помимо волевого решения эксперта о выборе рационального числового аналога заданной им качественной шкалы (настройки числовой шкалы), целесообразно применять следующую эвристическую процедуру, использующую обучающие выборки значений псевдослучайных коэффициентов ценности ЧДП. Пусть в задаче рассматривается n ЧДП {py, y=1, …, n}. С помощью программного генератора псевдослучайных чисел порождается m множеств {Wx, x=1, …, m} по n чисел в каждом со случайными значениями их коэффициентов сравнительной ценности {wxy, x=1, …, m, y=1, …, n, Затем эксперт может явно задать k1 числовых аналогов используемой качественной шкалы, например, шкалы на основе соотношений (2) и (3), шкалы {0; 0,167; 0,334; 0,501; 0,668; 0,835; 1,002}, {0; 0,166; 0,332; 0,498; 0,664; 0,83; 0,996}, после чего алгоритмически формируются k2=k–k1 дополнительных числовых шкал. В итоге на базе каждой матрицы {Mкx, x=1, …, m} формируется k=k1+k2 матриц {Mчxz, z=1, …, k} числовых парных оценок сравнительной значимости ЧДП, используемых для реконструкции их коэффициентов сравнительной ценности {wxy, x=1, …, m, y=1, …, n}, в результате чего формируются множества {Wвxz, x=1, …, m, z=1, …, k} восстановленных коэффициентов сравнительной ценности {wвxyz, x=1, …, m, y=1, …, n, z=1, …, k} ЧДП. Числовая оценка значимости ЧДП pf в сравнении с pi на базе z-й числовой шкалы размещается в ячейке mхz(f, i) матрицы Mчxz, а восстановленный коэффициент сравнительной ценности wвxfz ЧДП pf вычисляется суммированием элементов f-й строки Мxz, что имеет смысл суммарной меры доминирования по ценности ЧДП pf остальных ЧДП задачи. Затем для всех числовых шкал z=1, …, k вычисляются суммарные расхождения {Sz} истинных и восстановленных значений коэффициентов сравнительной ценности в виде:
Для выбора рационального аналога заданной качественной шкалы предлагается использовать следующий алгоритм автоматической генерации числовых шкал. 1. Экспертом задается число k2=k–k1 алгоритмически формируемых числовых шкал, аналогичных выбранной качественной шкале, минимально допустимая разница δ между соседними значениями числовых шкал, а также величина шага изменения исходной шкалы stpÎ[0,001; 0,05], например 0,01. На практике δ задается равной не менее трети расстояния между значениями равномерной числовой шкалы. 2. На основе равномерной шкалы, найденной с помощью соотношений (2), формируется множество числовых шкал со значениями: 2.1. {0; 2.2. {0; 2.3. {0; 2.4. {0; где При изменении значений формируемой шкалы на stp оценивается близость ее соседних значений {δi–1, i, i=2, …, nзн+1}. Если существует пара значений δi–1,i<δ, то шкала отбрасывается, изменение соответствующей переменной i(j) прекращается и переходят к формированию другой числовой шкалы. С ростом m и k будет расти и адекватность найденной числовой шкалы выбранной качественной шкале. Рациональный вариант шкалы при увеличении m и k будет стремиться к ее наилучшему варианту, а величина qi®min. Данный алгоритм синтеза числовых шкал и их проверки легко программируется. Изложенный подход позволяет найти рациональные числовые аналоги качественных парных оценок, приписав им наиболее адекватные значения, количественно характеризующие степень доминирования одних ЧДП над другими по ценности. Суммарная степень доминирования по ценности wk ЧДП pk над остальными ЧДП находится путем арифметического суммирования числовых бинарных оценок его сравнительной значимости: wk= При наличии nэ экспертов результирующий коэффициент ценности wk ЧДП pk определяется путем усреднения коэффициентов wmk, полученных этими экспертами, то есть Wk= Свойства (1) позволяют запрашивать у эксперта n´(n–1)/2 оценок {Rк(px, py), x=1, …, n–1; y=x+1, …, n} вместо n2 оценок {Rк(px, py), x=1, …, n; y=1, …, n}. Известно, что при парном сравнении ценности нескольких объектов, в том числе ЧДП, возникают две основные проблемы. 1. Значительная психологическая нагрузка на эксперта, от которого требуется безошибочно определять соотношение ценности десятков или сотен пар объектов. При сравнении ценности 10 ЧДП для получения множества оценок эксперту должно быть предъявлено 45 пар ЧДП, а при 30 ЧДП – уже 435 пар. 2. Появление непреднамеренных ошибок, неточностей и противоречий в экспертных оценках сравнительной ценности пар ЧДП, что приводит к порождению внутренне противоречивых систем бинарных оценок и возникновению неконтролируемых погрешностей при вычислении коэффициентов ценности, способных привести к ошибочным выводам, а также сложность выявления этих ошибок. Для снижения остроты этих проблем в [1, 2] предложено задавать на множествах пар качественных {(Rк(pm, px), Rк(px, pi)), m=1, ..., n, x=1, ..., n, i=1, ..., n, m≠i, x≠i, m≠x} и сопряженных числовых оценок {(Rч(pm, px), Rч(px, pi))} ОЧТ вида
Здесь «*» обозначает операцию композиции пар бинарных оценок. Анализ Rк и сущность традиционного отношения транзитивности позволили описать типовое ОЧТ между парами бинарных оценок, измеренных в рассмотренной семизначной качественной шкале (табл. 1). Прочерками в таблице обозначены ситуации, когда без участия эксперта невозможно определить значение оценки Rк(pm, pi) на основе оценок {(Rк(pm, px), Rк(px, pi)), x=1, ..., n, i≠m, x≠m, x≠i}. Таблица 1 Типовое ОЧТ качественных оценок Rк сравнительной значимости пар ЧДП
Из таблицы 1 видно, что для данного ОЧТ неопределенный результат имеет место менее чем в 45 % случаев, что позволяет значительно сократить объем диалога с экспертом, необходимого для формирования полного множества парных оценок, а также снизить потенциальную противоречивость этих систем оценок. Таблица 1 задает ОЧТ парных оценок усредненно, без учета особенностей конкретной диагностической задачи, возможностей и предпочтений эксперта. Поэтому в принципе она может претерпеть те или иные изменения, например, отраженные в таблице 2. Таблица 2 Возможные изменения ОЧТ оценок Rк сравнительной значимости пар ЧДП
Эксперт на основе своего опыта и особенностей решаемой задачи может использовать данные таблиц 1 и 2 или задать ОЧТ каким-то иным образом. Несмотря на описанный способ снижения противоречивости формируемых систем парных оценок, все-таки сохраняется потенциальная возможность внесения экспертом элементов противоречивости в них в случаях, когда он явно задает результат сравнения ценности пар ЧДП. Для минимизации противоречивости формируемых систем парных оценок предлагается следующий алгоритм. Шаг 1. Экспертом задается ОЧТ парных оценок, например, с помощью таблиц 1, 2. Шаг 2. Для определения очередной качественной оценки Rк(pm, pi) результата сравнения значимости ЧДП pm и pi с помощью заданного ОЧТ анализируются все пары оценок вида {(Rк(pm, px), Rк(px, pi)), x=1, ..., n, i≠m, x≠m, x≠i}. Шаг 3. Если ни одной пары (Rк(pm, px), Rк(px, pi)) ранее заданных или вычисленных оценок, для которых в ОЧТ определен результат их композиции, не найдено, то оценка Rк(pm, pi) запрашивается у эксперта, для чего переходим к шагу 4; если найдена одна или несколько результирующих оценок, переходим к шагу 7. Шаг 4. Эксперт задает результат сравнения (значение) Rк(pm, pi). Шаг 5. После задания экспертом оценки Rк(pm, pi) изучается ее возможная противоречивость ранее найденным оценкам. Для этого анализируются все пары оценок вида {(Rк(pk, pm), Rк(pm, pi)), (Rк(pm, pi), Rк(pi, pk)), k=1, ..., n, k≠m, k≠i} и с помощью заданного ОЧТ последовательно предпринимаются попытки вычисления значений всех оценок вида {Rк(pk, pi), k=1, ..., n, k≠i} и {Rк(pm, pk), k=1, ..., n, m≠k}. Шаг 6. Если хотя бы одна из найденных на шаге 5 оценок {Rк(pk, pi)} и {Rк(pm, pk)} противоречит ранее сформированной, эксперту предлагается вернуться к шагу 4 и задать для оценки Rк(pm, pi) другое значение. При отсутствии противоречий оценка Rк(pm, pi) считается допустимой и на основании (1) вычисляется симметричная ей оценка Rк(pi, pm). После этого переходят к поиску значения следующей оценки. Шаг 7. Если найдена только одна пара (Rк(pm, px), Rк(px, pi)) ранее сформированных оценок, для которых с помощью ОЧТ задан результат их композиции, он автоматически становится значением оценки Rк(pm, pi) без обращения к эксперту. Затем на основании соотношений (1) вычисляется значение оценки Rк(pi, pm). Если пар оценок {(Rк(pm, px), Rк(px, pi))}, для которых применимо заданное ОЧТ, найдено несколько и результаты применения к ним ОЧТ не совпадают, что свидетельствует о наличии скрытых противоречий в формируемой системе парных оценок, эксперту предлагается явно определить оценку Rк(pm, pi), выбрав для этого одно из значений, найденных на шаге 2. Частная методика расчета коэффициентов ценности ЧДП является важным элементом методики комплексной сравнительной оценки ПФС различных контингентов, обследуемых в фиксированный момент и во временной динамике с помощью отдельных интегральных показателей и их систем [1, 2], и может использоваться для выработки и повышения обоснованности принимаемых решений. Такие задачи возникают в ходе медицинской и психологической диагностики, при профессиональном отборе кандидатов на должности и учебу, в процессе обучения и профессиональной деятельности специалистов, при оценке состояния здоровья различных категорий обследуемых, в клинической практике. К достоинствам рассмотренной методики можно отнести: - ясный содержательный смысл используемых качественных и сопряженных с ними числовых измерительных шкал; - возможность адаптации применяемых качественных шкал и их числовых аналогов с учетом измерительных способностей экспертов и особенностей решаемых диагностических задач; - хорошую интерпретируемость и интуитивную понятность полученных результатов и используемых вычислительных процедур; - низкую вычислительную сложность большинства используемых вычислительных процедур методики и простые алгоритмы расчета; - отсутствие в методике вычислительных процедур и алгоритмов, понимание которых требует от пользователей глубоких знаний в теории измерений, математической статистике, матричной алгебре, теории многокритериального принятия решений; - использование для формирования внут- ренне непротиворечивых систем парных оценок и снижения нагрузки на экспертов описанного ОЧТ и дополнительных алгоритмических средств снижения противоречивости формируемых оценок. Часть изложенных в статье результатов была получена и апробирована автором в рамках диссертационного исследования, а также опубликована в печати [1, 2]. Ключевые элементы рассматриваемой частной методики реализованы в комплексе прикладных программ «Автоматизированная система для расчета интегральных показателей оценки психического и физиологического состояния человека (свид. об офиц. регистр. прогр. для ЭВМ № 2003611034, авторы: А.Е. Ермаков, К.А. Найденова, Н.М. Григорьева). Программы написаны на алгоритмическом языке Microsoft Visual Basic 6.0 Service Pack 6 с использованием библиотеки объектов FastLib 2000, снабжены контекстно-зависимой справочной системой на базе файлов форма- та html. Рассмотренная частная методика реализована в виде двух подсистем автоматизированной системы: подсистемы формирования множества оценок сравнительной важности пар ЧДП, обеспечивающей пользователю возможность задания пар сопряженных качественных и числовых измерительных шкал для парного сравнения ценности ЧДП, адекватных решаемой задаче и его измерительным возможностям, а также подсистемы формирования множества ЧДП, областей их допустимых значений и расчета коэффициентов сравнительной ценности. Литература 1. Ермаков А.Е. Методика сравнительной оценки психического и физиологического состояния обследуемых с помощью систем интегральных показателей. В кн.: Актуальные проблемы военной медицины: избран. тр. НИЦ академии // Вестник Рос. воен.-мед. акад. 2009. № 3(27). С. 60–67. 2. Ермаков А.Е., Найденова К.А. Интегральная оценка психологических и физиологических параметров человека // Проблемы реабилитации. 2001. № 1(4). С. 132–139. 3. Дэвид Г. Метод парных сравнений. М.: Статистика, 1978. 144 с. 4. Саати Т. Принятие решений. Метод анализа иерархий. М.: Радио и связь, 1993. 320 с. 5. Толстова Ю.Н. Измерение в социологии: курс лекций. М.: ИНФРА, 1998. 224 с. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2645&lang= |
Версия для печати Выпуск в формате PDF (6.26Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2010 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Методика комплексной сравнительной оценки психофизиологического состояния обследуемых
- Метод формирования приоритетного перечня автоматизируемых органов управления в системах специального назначения и его программная реализация
- Автоматизированная система прогнозирования остаточного ресурса электроконтактных соединений
- Автоматизированная система управления транспортировкой жидкой углекислоты по трубопроводу
- Автоматизированная система управления процессами создания наукоемких машиностроительных изделий
Назад, к списку статей



 . При парном сравнении ценности n ЧДП может существовать ЧДП pk, который в максимальной степени доминирует по ценности над всеми другими ЧДП, при этом его нормированный коэффициент сравнительной ценности wk=1. Этот wk получен суммированием n–1 максимального числового аналога z качественной парной оценки сравнительной значимости ЧДП и результата сравнения ценности pk с собой, равного 0,5z, то есть (n–1)z+0,5z=1, откуда
. При парном сравнении ценности n ЧДП может существовать ЧДП pk, который в максимальной степени доминирует по ценности над всеми другими ЧДП, при этом его нормированный коэффициент сравнительной ценности wk=1. Этот wk получен суммированием n–1 максимального числового аналога z качественной парной оценки сравнительной значимости ЧДП и результата сравнения ценности pk с собой, равного 0,5z, то есть (n–1)z+0,5z=1, откуда  .
. (результат сравнения px по ценности с собой для предотвращения ситуации, когда wx=0). Числовым аналогом качественной парной оценки ЗМЦ будем считать 0, а ЗБЦ – значение
(результат сравнения px по ценности с собой для предотвращения ситуации, когда wx=0). Числовым аналогом качественной парной оценки ЗМЦ будем считать 0, а ЗБЦ – значение 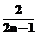 . Rч(px, py)=0 означает полную доминируемость по ценности ЧДП px показателем py. При этом py максимально доминирует над px (является в максимальной степени более ценным). Остальные nоц–2 оценки (5 при шкале с nоц=7) будут как-то распределены в
. Rч(px, py)=0 означает полную доминируемость по ценности ЧДП px показателем py. При этом py максимально доминирует над px (является в максимальной степени более ценным). Остальные nоц–2 оценки (5 при шкале с nоц=7) будут как-то распределены в 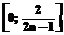 , причем пары противоположных оценок будут равноудалены от центрального значения
, причем пары противоположных оценок будут равноудалены от центрального значения  .
. .
.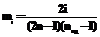 , i=0, …, nоц–1, откуда получаем соотношения
, i=0, …, nоц–1, откуда получаем соотношения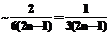 ,
,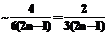 ,
, , (2)
, (2)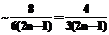 ,
,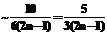 ,
, .
. ,
,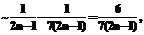
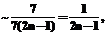 (3)
(3)
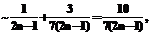
 .
.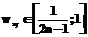 }. Далее ЧДП {py, y=1, …, n} для каждого Wx попарно сравниваются экспертом, знающим истинные значения {wxy}, с помощью априори заданной им качественной шкалы, допустим, описанной семизначной, отношения частичной транзитивности (ОЧТ) качественных парных оценок и иных процедур. На основе сравнения пар ЧДП формируются m матриц качественных парных оценок их сравнительной значимости {Mкx, x=1, …, m} размером n×n.
}. Далее ЧДП {py, y=1, …, n} для каждого Wx попарно сравниваются экспертом, знающим истинные значения {wxy}, с помощью априори заданной им качественной шкалы, допустим, описанной семизначной, отношения частичной транзитивности (ОЧТ) качественных парных оценок и иных процедур. На основе сравнения пар ЧДП формируются m матриц качественных парных оценок их сравнительной значимости {Mкx, x=1, …, m} размером n×n.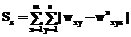 или
или 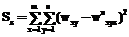 . Лучшим аналогом заданной качественной шкалы в рамках предлагаемого алгоритма будет считаться i-я числовая шкала:
. Лучшим аналогом заданной качественной шкалы в рамках предлагаемого алгоритма будет считаться i-я числовая шкала:  , z=1, …, k. Для нее средняя ошибка θi реконструкции коэффициентов сравнительной ценности {wxy} будет равна
, z=1, …, k. Для нее средняя ошибка θi реконструкции коэффициентов сравнительной ценности {wxy} будет равна 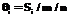 .
. –i×stp;
–i×stp;  –j×stp;
–j×stp; 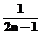 ;
;  +j×stp;
+j×stp; 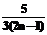 +i×stp;
+i×stp;  };
}; +j×stp;
+j×stp;  ;
; 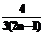 –j×stp;
–j×stp;  –i×stp;
–i×stp;  };
};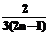 –j×stp;
–j×stp; 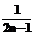 ;
;  –i×stp;
–i×stp;  };
};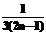 –i×stp;
–i×stp;  +j×stp;
+j×stp;  +i×stp;
+i×stp; 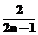 },
},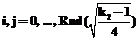 , i+j>0, Rnd(z) – операция округления величины z до ближайшего целого числа.
, i+j>0, Rnd(z) – операция округления величины z до ближайшего целого числа.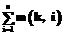 , где m(k, i) – бинарная оценка значимости ЧДП pk в сравнении с ЧДП pi; n – количество ЧДП.
, где m(k, i) – бинарная оценка значимости ЧДП pk в сравнении с ЧДП pi; n – количество ЧДП.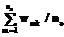 .
.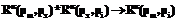 ,
, .
.