Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Модели производительности различных групп пользователей в человеко-компьютерном взаимодействии
Аннотация:Для исследования такого базового аспекта взаимодействия человека и компьютера, как производительность при выполнении быстрых прицельных движений, авторами предложена модель, основанная на законе Фиттса, который был расширен путем учета персональных характеристик пользователей – факторов возраста и пола. Полученные результаты могут использоваться при проектировании компьютерных интерфейсов, доступных всем группам пользователей.
Abstract:In research of a fundamental human-computer interaction component, such as throughput in making rapid aimed movements, a model is proposed based on Fitts’ law, which was extended by considering users personal characteristics – the factors of age and gender. The experimental results obtained in the paper may be used in designing universally accessible computer interfaces.
| Авторы: Авдеенко Т.В. (mesya@list.ru) - Новосибирский государственный технический университет, доктор технических наук, Бакаев М.А. (maxis81@gmail.com) - Новосибирский государственный технический университет (старший научный сотрудник), Новосибирск, Россия, кандидат технических наук | |
| Ключевые слова: проектирование интерфейсов, индекс производительности, закон фиттса, человеко-компьютерное взаимодействие |
|
| Keywords: interface design, movement throughput, Fitts’ law, human-computer interaction |
|
| Количество просмотров: 11666 |
Версия для печати Выпуск в формате PDF (5.09Мб) Скачать обложку в формате PDF (1.32Мб) |
По мере удешевления компьютерной техники и доступа к сети Интернет финансовый фактор все менее является аргументом против использования информационных технологий, по крайней мере, для жителей крупных и средних городов. На первый план выходит проблема сложности взаимодействия с компьютерами, обусловленная тем, что при проектировании многих современных интерфейсов недостаточно учитываются потребности и индивидуальные характеристики пользователей. В статье рассматривается метод моделирования способности совершать быстрые прицельные движения при работе с подавляющим большинством современных интерфейсов различными группами пользователей. Метод основывается на такой широко используемой в сфере человеко-компьютерного взаимодействия (ЧКВ) закономерности, как закон Фиттса [1], который авторами данной работы был расширен с учетом факторов возраста, пола и опыта. Моделирование выявляет важность учета характеристик различных групп пользователей и предлагает разработчикам интерфейсов полезный математический инструментарий. Метод моделирования Закон Фиттса [1], лежащий в основе моделирования в сфере ЧКВ, является одной из наиболее важных и широко признанных эмпирических данностей, описывающих поведение человека на психомоторном уровне. Общепринятая формулировка закона Фиттса следующая: MT=a+b*ID=a+b log2(A/W+1), (1) где MT – время, затрачиваемое на выполнение быстрого прицельного движения; A – расстояние, на которое производится движение; W – допустимое отклонение или размер области, в пределах которой движение должно быть завершено; a и b – константы, определяемые по результатам эксперимента. Величина ID=log2(A/W+1) измеряется в битах и называется индексом сложности движения. Наряду с индексом сложности полезной характеристикой в различных исследованиях является индекс производительности IP=ID/MT (сложность, приходящаяся на единицу времени). В настоящей работе исследуется влияние различий, присущих группам пользователей, на время выполнения ими заданий MT, а также на производительность. При этом авторы пользуются уточненной формулировкой закона Фиттса, учитывающего не только сложность, но и точность выполнения движения. Методика уточненного исследования приведена в работе [2] и состоит в том, что фиксированные расстояние A и размер цели W в соотношении (1) заменяются так называемыми эффективным расстоянием Ae и эффективным размером цели We. Эффективные характеристики получаются с учетом реально полученных в ходе эксперимента показателей. Эффективный размер цели вычисляется как We= Введенный Фиттсом индекс производительности IP называют просто производительностью и обозначают TP (throughput). Производительность TP рассчитывается как усредненная производительность каждого из K участников, которая, в свою очередь, вычисляется как среднее значение отношения эффективного индекса сложности IDe к затраченному на движение времени MT для каждого из M возможных сочетаний значений независимых переменных A и W:
Рассчитанная с использованием эффективного индекса сложности производительность является объективной и полной характеристикой, учитывающей как скорость, так и точность выполнения движения для заданных условий эксперимента. Такой подход к сравнению характеристик различных интерфейсных устройств является общепринятым и зафиксирован в стандарте ISO 9241-9:2000(E), которым при проведении исследований закона Фиттса руководствуется все больше научных групп (были рассчитаны значения производительности для манипулятора мышь (3,7–4,9), шарового манипулятора трекбол (1,0–2,9), джойстика (1,6–2,6) [2]). Производительность может быть критерием при сравнении не только интерфейсных устройств, но и прочих факторов. В настоящей работе закон Фиттса и показатель производительности применяются для исследования способности представителей различных групп пользователей, выделяемых исходя из возраста, пола и опыта, к совершению быстрых прицельных движений посредством манипулятора мышь. Экспериментальное исследование. Анализ данных В исследовании принимали участие две группы пользователей. Первую группу составляли 15 пожилых людей (4 мужчины и 11 женщин в возрасте от 56 до 74 лет, среднее значение – 63,4, среднеквадратичное отклонение – 5,26). Вторую – 13 молодых людей (5 мужчин и 8 женщин в возрасте от 17 до 30 лет, среднее значение – 23,9, среднеквадратичное отклонение – 4,38). Для участников эксперимента на мониторе отображались квадратные объекты, соответствующие начальной позиции движения и цели (размера W на расстоянии A). Значения A и W выбраны так, чтобы получить 7 различных значений индекса сложности от 1,58 до 7,01. Задание заключалось в том, чтобы кликнуть при помощи указателя компьютерной мыши на начальной позиции, а затем по возможности быстро и точно переместить указатель к цели и кликнуть на ней; при этом фиксировались затраченное на движение время MT и точные координаты обоих кликов (при непопадании в цель фиксировалась ошибка). Если текущий уровень ошибок E превосходил 10 %, участнику выдавалось сообщение с рекомендацией повысить точность выполнения задания. Поскольку для каждого из 7 значений ID предусматривалось 15 исходов, количество исходов для каждого участника составило 105, а общее количество полученных наборов данных – 2940. При предварительном анализе достоверности данных были отброшены 52 исхода (1,77 %), в ходе которых участник совершил явно ошибочный клик далеко от цели или же время выполнения задания превысило 3000 мс, то есть движение не может считаться быстрым, как того требовали задание и закон Фиттса. Среди достоверных результатов уровень ошибок, то есть промахов, составил 6 %, что приближается к предполагаемому номинальному уровню точности 96 %. Среднее время движения составило 922 мс, среднеквадратичное отклонение – 503. Средние значения времени MT и уровни ошибок E для различных значений ID представлены в таблице.
Метод многофакторного дисперсионного анализа применялся для проверки влияния группы и пола участника на время движения MT, уровень ошибок E и производительность TP. В результате анализа было обнаружено весьма существенное влияние группы участника (молодые и пожилые) на время совершения движения MT (F1,2884=890,9; p<0,001), при этом среднее значение времени составило 1156 мс для пожилых участников и 642 мс для молодых. Влияние группы участника на E также оказалось значимым (F1,2884=11,7; p=0,001), при этом средний уровень ошибок составил 3,7 % для пожилых людей и 7,0 % для молодых. Существенное влияние как на MT (F1,2884=8,1; p=0,005), так и на E (F1,2884=17,3; p<0,001) оказал и фактор пола. Мужчины в среднем справлялись с заданием несколько быстрее (874 мс) женщин (923 мс). Средний уровень ошибок составил соответственно 3,4 % и 7,3 %. Значимого эффекта взаимодействия между независимыми переменными отмечено не было. Дополнительно дисперсионный анализ был применен только к данным, полученным для пожилых участников. Обнаружено значимое влияние опыта (F1,1523=121,4; p<0,001) и пола (F1,1523=9,3; p=0,002) на время движения MT. Среднее время составило 1016 мс для опытных пожилых людей и 1370 мс для неопытных. Среди пожилых участников мужчины затратили на выполнение зада- ния в среднем 1242 мс, в то время как женщины – 1144 мс. Эффект взаимодействия между опытом и полом также оказался значимым с точки зрения MT (F1,1523=6,8; p=0,01). Уровень ошибок существенно зависел от пола (F1,1523=16,2; p<0,001): мужчины в среднем допустили 1 % ошибок, женщины – 6,5 %. Влияние фактора опыта у пожилых людей на E также оказалось значимым на уровне p=0,06 (F1,1523=3,7), и малоопытные участники допустили меньше ошибок – 2,4 %, чем более опытные – 5,0 %. Для пожилых участников было также отмечено значимое взаимодействие между опытом и полом с точки зрения MT (F1,1523=6,8; p=,01). Полученные результаты говорят о том, что пожилые люди выполняли задание в среднем почти в два раза медленнее своих молодых коллег (что было ожидаемо), но при этом допустили почти в два раза меньше ошибок; причем пожилые люди с низким уровнем опыта были в два раза точнее своих более опытных сверстников. Также можно отметить, что если в целом в эксперименте мужчины справлялись с заданием быстрее женщин, то среди пожилых людей ситуация была обратной. При исследовании методом дисперсионного анализа влияния группы участника, пола и опыта на итоговую производительность TP, вычисляемую по формуле (2), было отмечено значимое влияние группы участника (F1,22=98,1; p<0,001) и уровня опыта (F1,22=10,9; p=0,003), в то время как для пола значимости обнаружено не было (F1,22=0; p=0,998). Среднее значение TP для пожилых людей составило 3,29 по сравнению с 6,06 для молодых. Опытные участники показали производительность, равную 4,93, в то время как малоопытные – 2,77. Среднее значение производительности TP для всех участников эксперимента составило 4,58 (среднеквадратичное отклонение – 1,46). Влияние изменяемых факторов A и W на зависимые переменные MT и E было проанализировано методом дисперсионного анализа для обеих групп участников. Как и ожидалось, расстояние до цели A существенно влияло на время MT и для пожилых, и для молодых людей. В то же время не было отмечено значимого влияния A на уровень ошибок E ни для пожилых (F6,1502=0,9; p=0,5), ни для молодых участников (F6,1336=1,2; p=0,29). Размер цели W, помимо существенного влияния на MT для обеих групп участников, также оказался значимым с точки зрения E как для пожилых (F4,1502=5,5; p<0,001), так и для молодых людей (F4,1336=2,7; p=0,03). Значимого эффекта взаимодействия между A и W отмечено не было ни для одной из групп участников. Полученные результаты свидетельствуют, что и A, и W, как и ожидалось согласно закону Фиттса, влияют на MT, однако уровень ошибок E зависит только от W, причем это справедливо как для молодых, так и для пожилых участников. Построение регрессионных моделей На основе полученных экспериментальных данных и с учетом их предварительного анализа были построены модели регрессии согласно закону Фиттса (1). При этом использовалась методика учета точности с помощью вычисления эффективного индекса сложности. Сначала вычислялись эффективные значения для расстояния Ae и размера We, затем на их основе – эффективные значения индекса сложности IDe, которые использовались вместо номинальных ID. В результате МНК-оценивания параметров были получены следующие уравнения регрессии отдельно для пожилых (MTпож) и молодых (MTмол) участников: MTпож=359+211*IDe, (3) MTмол=132+134*IDe. (4) Все коэффициенты в моделях (3) и (4) имели высокую степень значимости (p<0,001), но коэффициенты детерминации оказались относительно невысокими: R2=0,537 для (3) и R2=0,639 для (4). При построении расширенной регрессионной модели для описания MT на основе объединенных данных было решено учитывать дополнительные факторы – возраст участника T, поскольку предварительный анализ данных позволял предположить его высокую значимость, а также пол участника G (равен 0 для мужчин и 1 для женщин). Фактор пола оказался незначимым в регрессии (p=0,259) несмотря на то, что дисперсионный анализ показал его значимость, и был исключен из модели. В результате получено регрессионное уравнение: MT=162+154*IDe+9*T. (5) Все параметры в модели (5) показали высокую значимость (p<0,001), а коэффициент детерминации составил R2=0,694. Однако при анализе предположений регрессии были выявлены непостоянство дисперсии остатков, их автокорреляция по критерию Дарбина–Уотсона и плохое приближение к нормальному распределению. Поэтому было решено выполнить степенное преобразование зависимой переменной MTa. Значение a выбиралось исходя из минимизации критерия Колмогорова–Смирнова для MTα относительно нормального распределения и составило a=0,2. Расширенная модель была построена для объединенных экспериментальных данных, однако из выборки исключались участники эксперимента с низким уровнем опыта (чтобы элиминировать влияние этого фактора). В результате получена следующая модель: MT0,2=2,8+0,166*IDe+0,009*T. (6) При этом значение коэффициента детерминации в регрессии R2=0,764, а анализ остатков показал отсутствие постоянства дисперсии и автокорреляции. Наконец, была предложена регрессионная модель для вычисления производительности TP, учитывающая факторы возраста T, пола G и наличия низкого опыта LE (0 – для нормального уровня опыта участника, 1 – для низкого). Фактор пола оказался незначимым (p=0,481), что подтверждается результатами дисперсионного анализа, и на предварительном этапе был исключен из модели. Значимость двух других факторов оказалась высокой (p<0,001). В результате оценивания параметров по всей выборке получена модель TP=7,27–0,998*LE–0,053*T. (7) Данная модель показала достаточно высокий коэффициент детерминации, R2=0,924, следовательно, она может использоваться для прогнозирования производительности, достигаемой при совершении движений компьютерной мышью, с учетом возраста и опыта пользователя. Результаты исследования взаимодействия различных групп пользователей с компьютерами позволяют предположить применимость предлагаемого метода для решения данной задачи. При выполнении заданий по движению с использованием мыши различия в возрастной группе были значимы с точки зрения как времени движения, так и уровня ошибок. В среднем пожилые участники затратили почти в два раза больше времени на выполнение заданий, но показали при этом почти в два раза более высокую точность, чем их молодые коллеги. Подобные выводы о более низкой скорости выполнения движений пожилыми людьми подтверждаются, например, в [3]. Влияние фактора пола в эксперименте может быть признано существенно менее выраженным. Для времени движения как для пожилых, так и для молодых людей были предложены расширенная регрессионная модель (5) и ее усовершенствованный вариант (6) с использованием степенного преобразования зависимой переменной. Модель свидетельствует о негативном влиянии возраста на скорость выполнения быстрых прицельных движений. Средняя производительность движения TP, равная в данном эксперименте 4,58, согласуется с диапазоном 3,7–4,9, обычно отмечаемым в исследованиях по методологии ISO 9241-9. Однако для пожилых участников производительность составила лишь 3,29. Для выявления производительности была предложена регрессионная модель (7), в ней наблюдается негативное влияние возраста и низкого уровня опыта. Значимое влияние возраста на производительность также было отмечено, например в [3]. Проектировщикам интерфейсов при построении динамических интерфейсов, выборе пороговых значений времени реакции системы и прочего необходимо учитывать исследуемые факторы с целью увеличения производительности при ЧКВ. Литература 1. Fitts P.M. The information capacity of the human motor system in controlling the amplitude of movement // Journal of Experimental Psychology. 1954, Vol. 47(6), pp. 381–391. 2. Soukoreff R.W. & MacKenzie I.S. Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts’ law research // International Journal of Human-Computer Studies. 2004, Vol. 61, pp. 751–789. 3. Bohan M. & Chaparro A. Age-Related Differences in Performance Using a Mouse and Trackball // In Proc. Human Factors and Ergonomics Society 42nd Annual Meeting. 1998, pp. 152–155. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2713 |
Версия для печати Выпуск в формате PDF (5.09Мб) Скачать обложку в формате PDF (1.32Мб) |
| Статья опубликована в выпуске журнала № 1 за 2011 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:



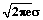 =4,133s, где s – среднеквадратическое отклонение для распределения точек завершения движений (предполагается нормальность соответствующего распреде- ления), а эффективное расстояние движения Ae может быть вычислено, например, как среднее расстояние от точки начала движения до конечных точек, получаемых в результате эксперимента. С использованием данных характеристик может быть вычислен эффективный индекс сложности IDe=log2(Ae/We+1).
=4,133s, где s – среднеквадратическое отклонение для распределения точек завершения движений (предполагается нормальность соответствующего распреде- ления), а эффективное расстояние движения Ae может быть вычислено, например, как среднее расстояние от точки начала движения до конечных точек, получаемых в результате эксперимента. С использованием данных характеристик может быть вычислен эффективный индекс сложности IDe=log2(Ae/We+1).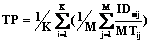 . (2)
. (2)