Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Факторный анализ в задачах моделирования многомерных систем
Аннотация:Рассматриваются вопросы идентификации многомерных стохастических систем и прогнозирования выходных сигналов. Для снижения размерности задачи предлагается использовать методы факторного анализа и фильтр Калмана. Построены алгоритмы идентификации и получены уравнения для параметров объектов.
Abstract:The problems of identification of multidimensional stochastic systems and predict the output signals. To reduce the dimension of the problem is proposed to use the techniques of factor analysis and Kalman filter. Algorithms to identify and obtain equations for the parameters of the objects.
| Авторы: Пащенко Ф.Ф. (feodor@ipu.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва, доктор технических наук, Дургарян И.С. (durgoft@ipu.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва, кандидат технических наук, Голяк И.В. (ivgo@bk.ru) - Институт проблем управления им. В.А. Трапезникова РАН, г. Москва | |
| Ключевые слова: корреляция, модель, факторный анализ, факторы, прогноз, идентификация, динамический объект, многомерный объект |
|
| Keywords: correlation, mathematical model, factor analysis, factors, the forecast, identification, a dynamic object, multidimensional object |
|
| Всего комментариев: 1 Количество просмотров: 16174 |
Версия для печати Выпуск в формате PDF (5.09Мб) Скачать обложку в формате PDF (1.32Мб) |
В процессе создания АСУ нередко некоторые параметры, характеризующие объект и входные процессы, недоступны для наблюдения или не могут быть автоматически измерены из-за отсутствия требуемых датчиков. В таких случаях приходится измерять не искомую величину, а ее косвенные показатели, которые можно контролировать автоматически. Подобные задачи возникают, например, при идентификации иерархических систем, когда взаимосвязи между элементами одного и того же или разных уровней фактически недоступны для наблюдения. Аналогичные ситуации складываются во многих областях промышленности, в экономике, социологии, медицине. Возникает задача построения многоступенчатого алгоритма прогнозирования, что при большой размерности вызывает значительные трудности. Эти трудности и размерность задачи можно существенно уменьшить, используя методы факторного анализа и дисперсионной идентификации. Пусть X(t) – входной сигнал, Y(t) – выходной сигнал идентифицируемого объекта, V(t) – выходной сигнал объекта с известным оператором B, A – оператор идентифицируемого объекта. Предположим, что оператор B имеет ограниченный обратный оператор B–1, тогда ненаблюдаемый входной сигнал можно представить в виде X(t)= =B–1V(t). Уравнение для оценки оператора идентифицируемого объекта при этом можно записать следующим образом: Y(t)=CV(t), где C=A´B–1. Пусть операторы A и B являются линейными нестационарными интегральными операторами. Тогда оценку весовой функции идентифицируемого объекта можно найти из системы интегральных уравнений
Решая данную систему известными методами, получим оценки как для весовой функции, так и для сигнала на входе объекта. При рассмотрении объектов, на входе и выходе которых действуют случайные процессы, решение поставленной задачи можно получить из системы уравнений
где Ky(t, s), Kv(t, s) – известные корреляционные функции сигналов Y(t) и V(t) соответственно; Kx(t, l) – неизвестная корреляционная функция входного сигнала; w(t, t) – известная весовая функция, а g(t, t) – неизвестная. При идентификации нелинейных объектов, а также линейных объектов, на входе которых действуют случайные процессы с нелинейной внутренней структурой, целесообразно применять дисперсионные методы. При этом оценку весовой функции линейного в среднем приближения идентифицируемого объекта можно получить из системы уравнений
В данной системе уравнений предполагается, что входные и выходные процессы являются стационарными и стационарно связанными в дисперсионном смысле [1]. В факторном анализе основным предположением является равенство X=LF+E, (1) где X – вектор-столбец наблюдаемых переменных размерности p´1; L–p´k – матрица факторных нагрузок; F–k´1 – вектор-столбец факторов (k Уравнение (1) постулирует основные предположения факторного анализа о том, что множество наблюдаемых коррелированных переменных X, которые подчиняются многомерному нормальному распределению с корреляционной матрицей C размерности p´p, можно описать меньшим числом гипотетических переменных или факторов F и множеством независимых остатков E. Рассмотрим модель объекта с выходом Y и входом X=(X1, …, Xp). Если p велико, возникает желание сократить размерность модели, выразив ее входы через меньшее количество k
для некоррелированных факторов
для коррелированных факторов
где P – оцененная корреляционная матрица факторов, а матрица L определяется согласно [2]. Модель объекта будем искать по формуле
где B – вектор-столбец неизвестных коэффициентов размерности k´1. Коэффициенты вектора определим из условия минимума функционала
Подставляя (4) в (5) и дифференцируя полученное выражение по В, придем к уравнению
Решая (6) с учетом (2), получим
где Q=LTC–1 – матрица размерности k´p, а матрицы Kxx и Kxy определяются соответственно формулами Для коррелированных факторов получим
Следует отметить, что (7) и (9) получены при условии линейной связи между факторами и входными переменными. Если эта связь нелинейна, то в (7) и (9) вместо (8) будут входить матрицы, элементы которых – дисперсионные функции. Рассмотрим представление ненаблюдаемых входов при помощи модели пространства состояний [3]. Предположим, что некоторый дискретный векторный процесс Y(t) описывается разностным линейным уравнением, которое представимо в форме Yi=AYi–1+ГUi–1, i=0, 1, …, (10) где Yi–n´1 – вектор-столбец состояния системы в момент ti; Ui–1 – векторный гауссовский белый шум; A и Г – постоянные матрицы. Предполагается, что Yi – стационарный гауссовский процесс с заданным начальным состоянием Y0. Пусть процесс Y(t) является входом определенного динамического объекта, для которого требуется построить модель в виде
где Предположим, что в те же дискретные моменты ti вместо вектора Yi измеряется вектор Zi размерности r´1 (r£n), линейно связанный с вектором состояния Yi:
где H – постоянная матрица размерности r´n; Vi – векторный гауссовский белый шум. Вместо вектора Yi в (11) подставим его оценку, оптимальную в смысле некоторого критерия, полученную по наблюдаемому вектору Zi. Наилучшая среднеквадратическая оценка Yi=M{Yi/z1, …, zi} может быть получена при помощи дискретного фильтра Калмана:
где неизвестная матрица Bi определяется из условия минимума среднеквадратической ошибки [1]. Применяя рекуррентную процедуру оценивания, выразим
где I – единичная матрица размерности n´n, а матрицы B1, …, Bi определяются согласно [1]. Без ограничения общности предположим, что математические ожидания векторов Yi и Zi равны нулю для любого момента i; Подставляя в (11) вместо вектора Yi его оценку
где Zi – набор векторов (Zi, Zi–1, …, Z1); элементами матрицы Учитывая (14), формулу (15) можно выразить через корреляционные матрицы процессов Zi и Wi и процессов Zi и Zj, j=1, …, i. Поскольку применение рекуррентной процедуры и определение матриц B1, …, Bi в (14) являются достаточно трудоемкими, используем в (11) другую оценку ненаблюдаемого вектора Yi по наблюдаемым векторам Z1, …, Zi. Проведем следующее преобразование переменных:
Здесь Zi означает набор векторов (Z1, …, Zi). Полученные переменные Xi и Fi связаны соотношением Xi=HFi+Vi, которое по форме аналогично соотношению (11) и в то же время полностью укладывается в рамки модели классического факторного анализа. Используя формулу связи между наблюдаемыми переменными и факторными нагрузками (2), можно получить следующую оценку
Применяя теорию псевдообратных матриц, учитывая (11) и то обстоятельство, что в качестве критерия минимизации применяется квадратичный функционал, (18) можно записать в виде
где H+ – псевдообратная матрица; y – произвольный вектор; I – единичная матрица. В частном случае при y=0 формула (19) принимает вид
Таким образом, модель (15) может быть записана в виде
Матрица коэффициентов P, найденная из условия минимума среднеквадратичного отклонения
Положим, как и выше, математические ожидания Zi и Wi равными нулю. Тогда Из вышесказанного следует, что, используя методы факторного анализа и рекуррентного фильтра Калмана, можно существенно сократить размерность прогнозирующих моделей без ощутимой потери точности. Литература 1. Дисперсионная идентификация; [под ред. Н.С. Райбмана]. М.: Наука, 1981. 2. Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. М.: Финансы и статистика, 2000. 3. Казаков И.Е. Статистическая теория систем управления в пространстве состояний. М.: Наука, 1975. 4. Дургарян И.С., Пащенко Ф.Ф. Метод двухступенчатой идентификации в задаче оценки экономической эффективности АСУ // Автоматика и телемеханика. 1977. № 5. 5. Функциональный анализ; [под ред. С.Г. Крейна]. М.: Наука, 1972. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2714&lang=&lang=&like=1 |
Версия для печати Выпуск в формате PDF (5.09Мб) Скачать обложку в формате PDF (1.32Мб) |
| Статья опубликована в выпуске журнала № 1 за 2011 год. | Версия для печати с комментариями |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Прогнозирование временного ряда инфекционной заболеваемости
- Алгоритм идентификации параметров устройства для нагрева жидкости
- Применение метода многоступенчатой идентификации при разработке математических моделей социально-экономических систем
- Технология сравнения и идентификации растровых изображений линий
- Модель сервисного обслуживания компьютерных тренажеров военного назначения
Назад, к списку статей
Comments
автор: Кирилл [2011-05-26 11:31:48]1) Зачем приведены формулы, предшествующие формуле (1)? 2) Английский язык в аннотации не выдерживает никакой критики.
Оценка пользователя: 0 баллов



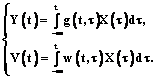
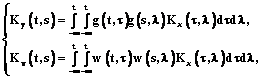
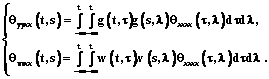
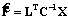 , (2)
, (2)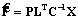 , (3)
, (3)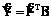 , (4)
, (4)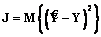 . (5)
. (5)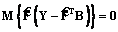 . (6)
. (6)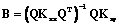 , (7)
, (7)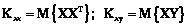 . (8)
. (8)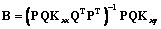 . (9)
. (9)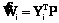 , (11)
, (11)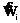 – выход модели в момент ti; P – вектор искомых коэффициентов модели.
– выход модели в момент ti; P – вектор искомых коэффициентов модели.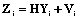 , (12)
, (12)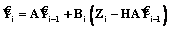 , (13)
, (13)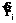 через оценку начального состояния
через оценку начального состояния 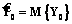 и значения наблюдаемых векторов Z1, …, Zi:
и значения наблюдаемых векторов Z1, …, Zi: (14)
(14)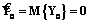 . Тогда справедливы равенства
. Тогда справедливы равенства 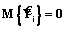 и
и 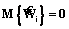 для любого i.
для любого i. и применяя аналогично предыдущему случаю среднеквадратический критерий для оценки вектора коэффициентов P, получим
и применяя аналогично предыдущему случаю среднеквадратический критерий для оценки вектора коэффициентов P, получим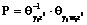 , (15)
, (15)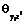 являются множественные дисперсионные функции, а элементами матрицы
являются множественные дисперсионные функции, а элементами матрицы 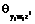 – множественные обобщенные дисперсионные функции.
– множественные обобщенные дисперсионные функции.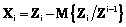 , (16)
, (16)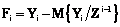 . (17)
. (17)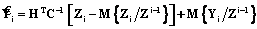 . (18)
. (18)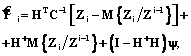 (19)
(19)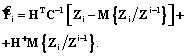 (20)
(20) (21)
(21)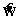 от W, имеет вид
от W, имеет вид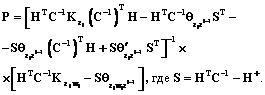 (22)
(22)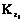 будет являться автокорреляционной матрицей векторного процесса Zi;
будет являться автокорреляционной матрицей векторного процесса Zi;  – взаимной корреляционной матрицей векторных процессов Zi и Wi;
– взаимной корреляционной матрицей векторных процессов Zi и Wi; 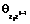 состоит из множества дисперсионных функций векторного процесса Zi относительно Zi–1;
состоит из множества дисперсионных функций векторного процесса Zi относительно Zi–1; 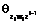 – из множественных обобщенных дисперсионных функций векторных процессов Zi и Wi относительно Zi–1;
– из множественных обобщенных дисперсионных функций векторных процессов Zi и Wi относительно Zi–1; 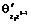 – из множественных дисперсионных функций векторных процессов Zi и Zi–1.
– из множественных дисперсионных функций векторных процессов Zi и Zi–1.