Структура многих NP-трудных задач комбинаторной оптимизации может быть описана гиперграфом. Такие задачи возникают в системах принятия решений, БД, при анализе информационных и коммуникационных сетей, конструкторском проектировании радиоэлектронной и вычислительной аппаратуры, лингвистической трансляции, при формировании трафика компьютерных сетей и т.д. Дерево декомпозиции гиперграфа дает возможность организовать процесс поиска оптимального решения по принципу «разделяй и властвуй». Если древовидная ширина гиперграфа ограничена сверху некоторой константой, то многие NP-трудные задачи комбинаторной оптимизации могут быть решены за полиномиальное время [1]. Древовидная ширина – это числовая характеристика гиперграфа, определяемая через оптимальное дерево декомпозиции. К сожалению, сама задача нахождения оптимального дерева деком- позиции также NP-трудная, поэтому в алгорит- мической практике востребованы эвристики, позволяющие получать хорошие деревья декомпозиции за разумное время.
В данной работе предлагается эвристический алгоритм CTDA (Computing Tree Decomposition by Acyclicity), основанный на пополнении гиперграфа до М-ациклического. Свойство М-ацикличности (называемое также a-ацикличностью) широко эксплуатируется в различных приложениях теории гиперграфов, так как обеспечивает полиномиальную вычислимость ряда важных характеристик и графических конструкций, связанных с гиперграфами [2–4]. Употребление данного свойства в алгоритме CTDA дает возможность создавать за полиномиальное время дерево декомпозиции гиперграфа с разной степенью приближения к оптимальному дереву декомпозиции.
Гиперграф и дерево декомпозиции. Используем терминологию и обозначения, принятые в [3–5]. Пусть задан гиперграф H=(X, U) с конечным множеством вершин X и ребер U. В общем случае U – конечное семейство произвольных подмножеств множества X. Гиперграф H=(Æ, Æ) считается пустым. Пусть U(x) – множество ребер, инцидентных в H вершине xÎX; X(u) – множество всех вершин, инцидентных в H ребру uÎU. Число ½U(x)½ определяет степень вершины x, а ½X(u)½ - степень ребра u. Элемент гиперграфа степени 0 считают голым, степени 1 – висячим. Два ребра u, vÎU кратны в H, если X(u)=X(v). Ребро u вложено в ребро v, когда X(u)ÌX(v). Гиперграф называется минимальным, если он не содержит голых элементов, вложенных и кратных ребер. Ранг гиперграфа H=(X, U) определяется как максимальная степень его ребра: r(H)=maxuÎU½X(u)½ .
Существуют различные способы задания гиперграфа. Так, если X={x1, x2, ..., xn}, n³1, и U={u1, u2, ..., um}, m³1, то (n, m)-гиперграф H=(X, U) однозначно описывается матрицей инциденций A(H)={aij}, где aij=1 при xiÎX(uj) и aij=0 при xiÏX(uj), i=1, 2, ..., n, j=1, 2, ..., m. Универсальным способом задания гиперграфа также является кенигово представление. Кенигово представление гиперграфа H=(X, U) – это обыкновенный двудольный граф K(H), отражающий отношение инцидентности различных элементов гиперграфа, с множеством вершин XÈU и долями X, U. Многие структурные свойства гиперграфа определяются через одноименные свойства кенигова представления. Так, гиперграф H считается связным, если граф K(H) связный. Далее в качестве исходных гиперграфов будем рассматривать, не нарушая общности, только непустые, минимальные и связные гиперграфы.
Частично структурные особенности гиперграфа H=(X, U) описывают ассоциированные с ним обыкновенные графы L(2)(H) и L(H). Граф L(2)(H) представляет отношение смежности вершин, а граф L(H) - отношение смежности ребер гиперграфа H. Граф L(H)=(U, E) полагают помеченным, если всякому его ребру {ui, uj}ÎE поставлена в соответствие метка fij=X(ui)ÇX(uj)¹Æ, 1£i
С гиперграфом связана еще одна графовая структура, именуемая деревом декомпозиции. Под деревом декомпозиции гиперграфа H=(X, U) понимают пару ({Xi, iÎI}, T=(I, E)), где {Xi, iÎI} – семейство мешков - непустых подмножеств множества X, T=(I, E) – дерево, удовлетворяющее условиям [1]:
· ÈiÎIXi=X, то есть множество мешков покрывает множество вершин гиперграфа;
· если uÎU, то всегда существует iÎI, такое, что X(u)ÍXi, то есть для всякого ребра гиперграфа всегда существует хотя бы один мешок, содержащий все вершины этого ребра;
· для любой вершины гиперграфа xÎX множество {iÎI | xÎXi} индуцирует связное поддерево дерева T=(I, E).
Ширина дерева декомпозиции ({Xi, iÎI}, T= =(I, E)) – наибольшая вместимость его мешка, уменьшенная на единицу, то есть maxiÎI{úXiú-1}. Древовидная ширина гиперграфа H (обозначается tw(H)) определяется как наименьшая ширина всех возможных деревьев декомпозиции, которые существуют для H. Дерево декомпозиции, ширина которого равна tw(H), принято называть оптимальным деревом декомпозиции. Древовидная ширина есть числовой параметр, характеризующий меру древовидности гиперграфа: чем меньше tw(H), тем ближе H к обычному дереву. Если H – несвязный гиперграф, то tw(H)=0. Следует отметить, что для каждого (n,m)-гиперграфа всегда существует хотя бы одно дерево декомпозиции. Например, таковым является тривиальное дерево декомпозиции, состоящее из одного узла с мешком X и имеющее ширину n–1. Ясно, что тривиальное дерево декомпозиции в общем случае не является оптимальным. Очевидны оценки: r(H)–1£tw(H), 0£tw(H)£n–1.
Характеризация М-ациклических гиперграфов. Пусть в (n,m)-гиперграфе H=(X, U) задана последовательность его ребер P=(u1, u2, ..., uk, uk+1), 3£k
В гиперграфе H последовательность P задает М-цикл длины k, если
1) u1, u2, ..., uk+1 – различные ребра гиперграфа H (различные как элементы семейства U);
2) каждые два соседних ребра в P смежные, то есть fi¹Æ, i=1, 2, ..., k;
3) fi¹fi+1, i=1, 2, ..., k;
4) u1=uk+1 и f1¹fk.
М-цикл P=(u1, f1, u2, f2, ..., uk, fk, uk+1) считается бесхордовым, когда для любой его тройки множеств fa, fb, fc, 1£a
Теорема 1. Для (n, m)-гиперграфа H=(X, U) следующие высказывания эквивалентны [2–4]:
1) H является М-ациклическим гиперграфом;
2) H комплектный, и его граф L(2)(H) триангулированный;
3) для H существует дерево соединений;
4) дерево соединений гиперграфа H – остовное дерево наибольшего веса взвешенного реберного графа L(H);
5) дерево клик графа L(2)(H) изоморфно дереву соединений гиперграфа H;
6) алгоритм Грэхема завершается успешно;
7) H не содержит блоков при условии, что H минимальный и úUú=m>1.
Данная теорема определяет свойства М-ациклического гиперграфа, используемые далее в алгоритме CTDA. Дадим краткие пояснения.
Пусть L(H)=(U, E) – взвешенный реберный граф гиперграфа H=(X, U) и Tjoin(H) – остовное дерево для L(H). Дерево Tjoin(H) называется деревом соединений гиперграфа H, если для всякой пары ui, ujÎU и любого xÎX(ui)ÇX(uj)¹Æ в Tjoin(H) существует x-путь P=(ui, ui+1, ..., uj), который следует из ui в uj и x лежит вдоль этого пути: xÎX(ui), xÎX(ui+1), …, xÎX(uj). Нетрудно убедиться, что для М-ациклического (n, m)-гиперграфа дерево соединений является оптимальным деревом декомпозиции, каждый мешок которого содержит вершины в точности одного ребра гиперграфа. Также ½I ½=m, tw(H)=r(H)-1. Из эквивалентности высказываний теоремы 1, пп. 1 и 4, вытекает полиномиальный по времени способ нахождения оптимального дерева декомпозиции для М-ациклического графа: построить взвешенный реберный граф L(H) и найти для него остовное дерево наибольшего веса. Распознать М-ацикличность можно с помощью алгоритма Грэхема [2].
Алгоритм Грэхема является элиминационной схемой последовательного применения к гиперграфу следующих операций: СУВ – слабое удаление висячих вершин (без удаления инцидентных им ребер); СУР – слабое удаление кратных, вложенных ребер (без удаления инцидентных им вершин). Обозначим через red(H) гиперграф, полученный в результате применения алгоритма Грэхема к гиперграфу H. Говорят, что алгоритм Грэхема для H завершается успешно, если red(H)=(Æ, Æ). Алгоритм Грэхема всегда приводит к одному и тому же гиперграфу red(H) независимо от порядка и числа удаляемых элементов на каждом шаге. Кроме того, операции СУВ и СУР сохраняют связность гиперграфа. Все это свидетельствует о рекурсивном характере алгоритма Грэхема и наследственности свойства М-ацикличности относительно операций СУВ и СУР (все гиперграфы, полученные из М-ациклического гиперграфа путем применения к нему этих операций, также М-ацикличны). Алгоритм Грэхема прост в реализации и имеет полиномиальную временную сложность. Операция СУР алгоритма Грэхема осуществляет минимизацию текущего гиперграфа.
Многие известные эвристические алгоритмы построения дерева декомпозиции гиперграфа опираются на свойства триангулированных графов [1]. Суть их в следующем: вначале для заданного гиперграфа H находится минимальная триангуляция графа L(2)(H) (минимальное пополнение L(2)(H) до триангулированного графа), а затем создается дерево клик для минимальной триангуляции. При этом структурные особенности самого гиперграфа H эксплуатируются лишь частично. Напомним, что граф называется триангулированным, если всякий его цикл длиной k³4 обладает хордой - ребром, соединяющим две несмежные вершины данного цикла (сам цикл при этом называется хордовым).
Описание и обоснование алгоритма. Эвристический алгоритм CTDA конструирует дерево декомпозиции путем минимального пополнения исходного гиперграфа до М-ациклического. Стратегия алгоритма CTDA: использование в полном объеме характеризации М-ациклических гиперграфов и информации о структуре исходного гиперграфа H=(X, U). Это достигается разделением процесса решения задачи на три этапа.
Этап 1. Уменьшение размерности решаемой задачи путем сокращения числа элементов исходного гиперграфа с помощью алгоритма Грэхема и выделения блоков гиперграфа.
Этап 2. Устранение в каждом блоке бесхордовых М-циклов путем добавления в H множества дополнительных ребер Uadd.
Этап 3. Построение для результирующего гиперграфа Hadd=(X, UÈUadd) дерева соединений, используя эквивалентность высказываний теоремы 1, пп. 1, 3, 4.
Алгоритм CTDA на этапе 2 применяет эвристику «минимальная степень». Поскольку предварительно на этапе 1 размерность задачи снижается, область действия погрешностей, вносимых эвристикой, сокращается. Это позволяет добавлять в H дополнительные ребра минимально необходимой мощности для устранения бесхордовых М-циклов и получать в итоге деревья декомпозиции с шириной, близкой к tw(H).
Дадим разъяснения к каждому из трех этапов алгоритма CTDA. Будем по-прежнему полагать, что исходный (n, m)-гиперграф H=(X, U) является непустым, минимальным и связным. Кроме того, будем исходить из того, что úUú=m>1 и m=O(nt), t³1, то есть число ребер гиперграфа полиномиально зависит от числа его вершин. Если H имеет только одно ребро, решение известно: тривиальное дерево декомпозиции гиперграфа H является оптимальным и tw(H)=n–1.
Пусть YÍX и Y=X(ui)ÇX(uj)=fij¹Æ для некоторой пары ребер ui, ujÎU гиперграфа H=(X, U), 1£i
Вначале Uadd=Æ. Если исходный гиперграф H=(X, U) является М-ациклическим, для него алгоритм Грэхема завершается успешно. Это означает, что в H нет нетривиальных блоков и бесхордовых М-циклов. Необходимости в выполнении этапа 2 нет – можно сразу перейти на этап 3 без изменения Uadd. Если оказалось, что гиперграф H=(X, U) М-циклический, то B=red(H) – непустой, минимальный и М-циклический гиперграф. Согласно высказыванию теоремы 1, п. 7, B=red(H) содержит хотя бы один нетривиальный блок. Найти все блоки гиперграфа B можно за время O(m2), используя для этого метки fij=X(ui)ÇX(uj)¹Æ помеченного графа L(B). В выделенных блоках возможно появление висячих вершин, а после их удаления – кратных и вложенных ребер. Также некоторые блоки могут быть тривиальными. Значит, к каждому блоку гиперграфа B=red(H) целесообразно вновь применить алгоритм Грэхема. Учитывая, что временная сложность алгоритма Грэхема для (n,m)-гиперграфа составляет O(nm) и m=O(nt), t³1, этап 1 алгоритма CTDA можно реализовать за время O(n2t).
Пусть B1, B2, …, Bs – блоки, выделенные из гиперграфа B=red(H) и подвергнутые обработке алгоритмом Грэхема так, что каждый из них есть непустой, минимальный, связный гиперграф. Поскольку гиперграф B=red(H) М-циклический, всякий блок Bi, i=1, 2, …, s, имеет хотя бы один бесхордовый М-цикл. Связь между бесхордовыми М-циклами гиперграфа и структурными свойствами графа L(2) устанавливает теорема 2, сформулированная применительно к Bi, i=1, 2, …, s.
Теорема 2. Для любого гиперграфа Bi верны следующие высказывания:
1) всякий бесхордовый М-цикл длины k=3 гиперграфа Bi порождает в L(2)(Bi) один или несколько соответствующих простых хордовых циклов длины k³3;
2) всякий бесхордовый М-цикл длины k>3 гиперграфа Bi порождает в L(2)(Bi) соответствующий простой цикл, не содержащий хорды и имеющий длину l>3 (k и l необязательно равны);
3) каждый простой цикл графа L(2)(Bi) длины k>3, не имеющий хорды, продуцирует в Bi соответствующий бесхордовый М-цикл длины k>3;
4) гиперграф Bi некомплектен тогда и только тогда, когда содержит хотя бы один бесхордовый М-цикл длины k=3.
Некоторые из утверждений теоремы 2 доказаны в [3], другие очевидны. Из построения Bi, i=1, 2, …, s, и теоремы 2 следует, что каждый блок Bi содержит не менее трех вершин и не менее трех ребер. В силу теорем 1, 2 и того, что Bi - непустой, минимальный, связный и М-циклический гиперграф, возможна одна из трех ситуаций.
Ситуация I. Гиперграф Bi некомплектен, а его граф L(2)(Bi) триангулированный.
В этом случае все бесхордовые М-циклы гиперграфа Bi имеют длину k=3.
Ситуация II. Гиперграф Bi комплектный, но граф L(2)(Bi) не является триангулированным.
В данном случае гиперграф Bi содержит бесхордовые М-циклы только длины k>3.
Ситуация III. Гиперграф Bi некомплектен, и L(2)(Bi) не является триангулированным графом.
В этой ситуации гиперграф Bi содержит хотя бы один бесхордовый М-цикл длины k=3 и не менее одного бесхордового М-цикла длины k>3.
Ситуация I самая простая. Поскольку граф L(2)(Bi) триангулированный, он содержит не более úXú=n максимальных клик и все они могут быть найдены за время O(n2). Если для какой-либо максимальной клики YÍX графа L(2)(Bi) в гиперграфе Bi нет такого ребра u, что YÍX(u), множество Y необходимо добавить в Uadd в качестве дополнительного ребра. Подобные ребра устраняют в Bi бесхордовые М-циклы длины k=3, точнее, они становятся хордами для этих циклов. Тем самым гиперграф Bi превращается в комплектный, а значит, и в М-ациклический гиперграф. Нетрудно убедиться, что хорды для Bi являются также хордами для соответствующих бесхордовых М-циклов исходного гиперграфа H.
Ситуацию I можно легко распознать с помощью свойств триангулированных графов: любой триангулированный граф имеет симплициальную вершину; свойство триангулированности не утрачивается при удалении из графа отдельной вершины. Вершина графа называется симплициальной, если ее окрестность – клика. Таким образом, если последовательный поиск в L(2)(Bi) симплициальных вершин и их удаление из L(2)(Bi) приводят к пустому графу, то L(2)(Bi) – триангулированный граф. Так как граф L(2)(Bi) содержит не более n вершин, распознать его триангулированность можно за время O(n2).
Ситуации II и III мало чем отличаются друг от друга, так как требуют прежде всего триангуляции графа L(2)(Bi) – приведения его к триангулированному графу. Процесс триангуляции графа L(2)(Bi) – это насыщение графа новыми ребрами (хордами), что может привести к появлению новых клик. Даже если гиперграф Bi ранее был комплектным, после триангуляции графа L(2)(Bi) он может утратить это свойство. Чрезвычайно важно выполнять триангуляцию графа L(2)(Bi) наилучшим образом.
 Пусть L(2)(Bi)=(V, W), VÍX, и Gi=(V, WÈ ÈWadd) - триангулированный граф, полученный насыщением графа L(2)(Bi) множеством хорд Wadd. Известно, что задача нахождения наименьшей триангуляции произвольного графа (наименьшего пополнения графа до триангулированного) является NP-трудной. Между тем триангуляцию хорошего качества можно всегда отыскать за время O(n3). Для этого достаточно воспользоваться эвристикой «минимальная степень». Суть ее в следующем: в графе L(2)(Bi) выбирается вершина наименьшей степени, ее окрестность дополняется до клики; затем данная вершина удаляется из L(2)(Bi). Указанные действия повторяются до тех пор, пока L(2)(Bi) не выродится в пустой граф. Эвристика «минимальная степень» в большинстве случаев дает триангуляцию, близкую к наименьшей триангуляции. Когда триангуляция Gi=(V, WÈWadd) для L(2)(Bi) построена, ситуации II и III вырождаются в ситуацию I. Поскольку число блоков для гиперграфа B=red(H) не превышает úUú=m>1, все действия этапа 2 алгоритма CTDA можно реализовать за время O(n3m) или при m=O(nt), t³1, за время O(nt+3).
Пусть L(2)(Bi)=(V, W), VÍX, и Gi=(V, WÈ ÈWadd) - триангулированный граф, полученный насыщением графа L(2)(Bi) множеством хорд Wadd. Известно, что задача нахождения наименьшей триангуляции произвольного графа (наименьшего пополнения графа до триангулированного) является NP-трудной. Между тем триангуляцию хорошего качества можно всегда отыскать за время O(n3). Для этого достаточно воспользоваться эвристикой «минимальная степень». Суть ее в следующем: в графе L(2)(Bi) выбирается вершина наименьшей степени, ее окрестность дополняется до клики; затем данная вершина удаляется из L(2)(Bi). Указанные действия повторяются до тех пор, пока L(2)(Bi) не выродится в пустой граф. Эвристика «минимальная степень» в большинстве случаев дает триангуляцию, близкую к наименьшей триангуляции. Когда триангуляция Gi=(V, WÈWadd) для L(2)(Bi) построена, ситуации II и III вырождаются в ситуацию I. Поскольку число блоков для гиперграфа B=red(H) не превышает úUú=m>1, все действия этапа 2 алгоритма CTDA можно реализовать за время O(n3m) или при m=O(nt), t³1, за время O(nt+3).
Этап 3 алгоритма CTDA включает в себя следующие действия: создание взвешенного реберного графа L(Hadd), построение для L(Hadd) остовного дерева наибольшего веса. Построенное дерево – дерево декомпозиции исходного гиперграфа H=(X, U). Все эти действия можно выполнить за время O(m2) или при m=O(nt), t³1, за время O(n2t). В целом алгоритм CTDA позволяет конструировать дерево декомпозиции гиперграфа H=(X, U) за время O(n2t). Это дерево может содержать узлы, мешки которых вложены. Если XiÌXj, то к ребру {i, j} в T=(I, E) можно применить операцию сжатия. Подобные действия сокращают число узлов построенного дерева декомпозиции ({Xi, iÎI}, T=(I, E)), не изменяя его ширины. Важно, что данный алгоритм допускает построение требуемого дерева с разной степенью приближения к оптимальному дереву декомпозиции.
1. Если H=(X, U) – М-ациклический гиперграф, созданное дерево декомпозиции является оптимальным и ширина этого дерева определяет tw(H).
2. На этапе 1 в Uadd можно сразу внести ребро, содержащее все вершины гиперграфа B=red(H). После этого гиперграф Hadd=(X, UÈUadd) станет М-ациклическим. Дерево соединений для Hadd - дерево декомпозиции исходного гиперграфа. Оно приемлемо, когда число вершин гиперграфа B=red(H) меньше r(H). Однако, если H=red(H), то, действуя подобным образом, получим тривиальное дерево декомпозиции.
3. На этапе 1 можно сформировать s более мелких дополнительных ребер, включив в каждое такое ребро все вершины из Bi, i=1, 2, …, s. Тем самым получим дерево декомпозиции меньшей ширины, чем в предыдущем случае.
4. Выполнение этапа 2 исчерпывает все возможности алгоритма CTDA по построению дерева декомпозиции гиперграфа.
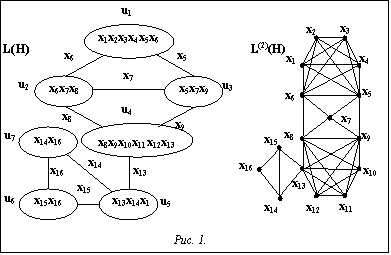
Иллюстрация работы алгоритма CTDA. Рассмотрим (16, 7)-гиперграф H=(X, U), который на рисунке 1 представлен помеченным реберным графом L(H) и графом L(2)(H). Ранг гиперграфа H равен 6.
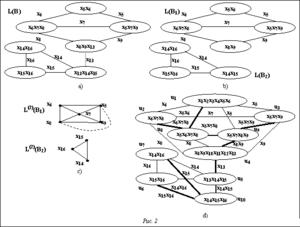 Процесс построения для H дерева декомпозиции изображен на рисунке 2 и включает в себя следующие действия.
Процесс построения для H дерева декомпозиции изображен на рисунке 2 и включает в себя следующие действия.
· Вначале Uadd=Æ. Ребра u1, u4ÎU содержат висячие вершины x1, x2, x3, x4, x10, x11, x12. Их слабое удаление дает гиперграф B=red(H). Единственным множеством сочленения гиперграфа B=red(H) является {x13}.
· Множество сочленения {x13} порождает два блока, в каждом из которых вершина x13 висячая. Слабое удаление этой вершины приводит к блокам B1 и B2.
· Блок B1 - некомплектный гиперграф, для которого граф L(2)(B1) нетриангулированный. После добавления в L(2)(B1) ребра {x5, x8} получаем минимальную триангуляцию графа L(2)(B1), содержащую две максимальные клики – {x5, x6, x7, x8} и {x5, x7, x8, x9}. В H нет ребер с таким составом вершин. Поэтому к Uadd добавляем ребра u8 и u9, где X(u8)={x5, x6, x7, x8} и X(u9)={x5, x7, x8, x9}. Блок B2 - некомплектный гиперграф, но граф L(2)(B2) триангулированный. Граф L(2)(B2) имеет одну максимальную клику {x14, x15, x16}. Для этой клики в H нет подходящего ребра. Добавляем в Uadd ребро u10, где X(u10)={x14, x15, x16}.
· Результирующий гиперграф Hadd=(X, UÈ ÈUadd) является М-ациклическим. Его помеченный реберный граф L(Hadd) изображен на рисунке 2d. Остовное дерево наибольшего веса для L(Hadd) (оно выделено на рисунке 2d жирными линиями) определяет дерево декомпозиции гиперграфа H=(X, U) ширины 5. Построенное дерево декомпозиции имеет узлы с вложенными мешками, поэтому возможно сокращение числа узлов этого дерева без изменения его ширины.
Заметим, что гиперграф B=red(H) имеет 9 вершин, что больше r(H). Однако блоки B1 и B2 состоят из 5 и 3 вершин соответственно. Это уже меньше r(H). После выделения блоков и без дальнейшего их анализа можно сразу образовать два дополнительных ребра – u¢8, u¢9, где X(u¢8)={x5, x6, x7, x8, x9} и X(u¢9)={x14, x15, x16}. Это приведет к дереву декомпозиции с меньшим числом узлов, чем на рисунке 2d, и той же ширины 5. Можно убедиться, что для заданного (16, 7)-гиперграфа H не существует дерева декомпозиции с шириной меньше 5. Таким образом, алгоритм CTDA в данном конкретном случае конструирует оптимальные деревья декомпозиции.
В заключение необходимо отметить, что представленный в работе эвристический алгоритм CTDA основан на характеризациях М-ациклических гиперграфов. В нем применяется эвристика «минимальная степень». Оптимальность алгоритма CTDA может быть потеряна только за счет этой эвристики. Основное преимущество алгоритма CTDA перед другими подобными алгоритмами - использование в полном объеме информации о структуре исходного гиперграфа. Алгоритм CTDA реализован в виде программы на языке C++. Вычислительные эксперименты показали, что алгоритм создает дерево декомпозиции, которое оптимально или близко к оптимальному, когда в исходном гиперграфе после предобработки алгоритмом Грэхема все ребра имеют приблизительно одну и ту же степень. Возможно включение в алгоритм CTDA новых эвристик, расширяющих область эффективного применения данного алгоритма.
Литература
1. Bodlaender H.L. Discovering treewidth. In Proceedings of the 31st Conference SOFSEM 2005, Springer-Verlag, Lecture
Notes in Computer Science 3381, 2005, pp. 1–16.
2. Мейер Д. Теория реляционных баз данных. М.: Мир, 1987.
3. Быкова В.В. Полиномиальные достаточные условия бихроматичности гиперграфа // Вест. КрасГУ: сер. Физ.-мат. науки. 2006. № 7. С. 98–106.
4. Быкова В.В. М-ациклические и древовидные гиперграфы // Изв. Томского политех. ун-та. 2010. Т. 317. № 2. С. 25–30.
5. Зыков А.А. Гиперграфы // Успехи математических наук. 1974. Т. 29. Вып. 6. С. 89–154.



 Пусть L(2)(Bi)=(V, W), VÍX, и Gi=(V, WÈ ÈWadd) - триангулированный граф, полученный насыщением графа L(2)(Bi) множеством хорд Wadd. Известно, что задача нахождения наименьшей триангуляции произвольного графа (наименьшего пополнения графа до триангулированного) является NP-трудной. Между тем триангуляцию хорошего качества можно всегда отыскать за время O(n3). Для этого достаточно воспользоваться эвристикой «минимальная степень». Суть ее в следующем: в графе L(2)(Bi) выбирается вершина наименьшей степени, ее окрестность дополняется до клики; затем данная вершина удаляется из L(2)(Bi). Указанные действия повторяются до тех пор, пока L(2)(Bi) не выродится в пустой граф. Эвристика «минимальная степень» в большинстве случаев дает триангуляцию, близкую к наименьшей триангуляции. Когда триангуляция Gi=(V, WÈWadd) для L(2)(Bi) построена, ситуации II и III вырождаются в ситуацию I. Поскольку число блоков для гиперграфа B=red(H) не превышает úUú=m>1, все действия этапа 2 алгоритма CTDA можно реализовать за время O(n3m) или при m=O(nt), t³1, за время O(nt+3).
Пусть L(2)(Bi)=(V, W), VÍX, и Gi=(V, WÈ ÈWadd) - триангулированный граф, полученный насыщением графа L(2)(Bi) множеством хорд Wadd. Известно, что задача нахождения наименьшей триангуляции произвольного графа (наименьшего пополнения графа до триангулированного) является NP-трудной. Между тем триангуляцию хорошего качества можно всегда отыскать за время O(n3). Для этого достаточно воспользоваться эвристикой «минимальная степень». Суть ее в следующем: в графе L(2)(Bi) выбирается вершина наименьшей степени, ее окрестность дополняется до клики; затем данная вершина удаляется из L(2)(Bi). Указанные действия повторяются до тех пор, пока L(2)(Bi) не выродится в пустой граф. Эвристика «минимальная степень» в большинстве случаев дает триангуляцию, близкую к наименьшей триангуляции. Когда триангуляция Gi=(V, WÈWadd) для L(2)(Bi) построена, ситуации II и III вырождаются в ситуацию I. Поскольку число блоков для гиперграфа B=red(H) не превышает úUú=m>1, все действия этапа 2 алгоритма CTDA можно реализовать за время O(n3m) или при m=O(nt), t³1, за время O(nt+3).
