Потребность в автоматизации формирования математических моделей сложных механических систем и в создании отечественного специализированного программного обеспечения с простым и удобным интерфейсом для широкого круга пользователей инженерного профиля сегодня наиболее высока. Прежде всего это связано с интенсивным развитием машиностроительной отрасли и высокой конкуренцией. Однако в отечественной и зарубежной литературе информация о теоретических основах и программной реализации используемых методик построения и визуализации динамических моделей либо отсутствует, либо ограниченна. Это создает определенные трудности при добавлении в элементную базу зарубежных программных комплексов новых элементов динамических моделей (ЭДМ) или при модификации свойств и характеристик базовых элементов. Кроме того, распространяемые в настоящий момент зарубежные САПР динамического анализа технических систем рассчитаны на высококвалифицированных специалистов, требуют прохождения специальных обучающих курсов, имеют высокую стоимость и не позволяют решать специфические задачи без дополнительной доработки элементной базы, к тому же поставляемая с ними справочная документация не переведена на русский язык. Вследствие этого зарубежные программные комплексы динамического анализа не получили широкого распространения в конструкторских отделах, и предприятия вынуждены заказывать выполнение проектных работ в отечественных организациях, специализирующихся в области динамического моделирования.
Представление структуры математической модели в матричной форме
При автоматизации формирования динамических моделей с использованием структурно-матричного метода [1] возникает необходимость в матричном (табличном) описании структуры моделируемого объекта. Заполнение элементов матриц осуществляется в соответствии с принятыми правилами кодирования имеющихся в модели элементов и упорядочения их связей. Автоматизация процесса заполнения элементов матриц требует разработки соответствующего алгоритма.
В данной работе предлагается алгоритм автоматизированного перехода от двухмерного графического представления динамической модели к матричному. Матричное представление моделей реализовано применительно к структурно-матричному методу моделирования технических систем на макроуровне [1, 2].
Формирование динамической модели осуществляется путем перемещения выбранного ЭДМ из палитры элементов на область построения динамических схем. Положение ЭДМ определяется двумя координатами. Каждый ЭДМ имеет полюсы, которые связываются между собой соединительными линиями (связями).
Формирование структуры математической модели в матричной форме заключается в представлении совокупности элементов динамической модели и связей между ними в виде матриц, причем для каждого вида ЭДМ предусмотрена своя матрица.
Матрица инерционных элементов принимается в качестве базисной. Она представляет собой единичную диагональную матрицу. Ее размерность равна количеству инерционных элементов.
Матрица внешних воздействий типа потенциала – таблица, количество строк которой равно количеству инерционных элементов, а количество столбцов – количеству внешних воздействий. Заполнение каждого элемента матрицы, находящегося на пересечении j-го столбца и i-й строки, происходит по следующему принципу: если j-е воздействие подводится к i-му инерционному элементу, элемент матрицы принимает значение единицы; если направление j-го воздействия не совпадает с направлением фазовой координаты типа потока (скорости) i-го инерционного элемента, элемент матрицы принимает значение –1; если j-е воздействие не приложено к i-му инерционному элементу, элемент матрицы принимает нулевое значение.
Для моделирования источников внешнего воздействия типа потенциала (силы и вращающие моменты) предусмотрен отдельный тип ЭДМ. Полюсы источника типа потенциала и инерционного ЭДМ соединяют линией связи. При описании внешнего воздействия пользователь задает знак воздействия, выбирает тип воздействия, его характеристику и вводит численные значения параметров.
Матрица упругих ЭДМ имеет размерность n´m, где n – число строк, равное количеству инерционных элементов; m – число столбцов, равное количеству упругих ЭДМ. Единицами отмечается наличие соединений между инерционными и упругими ЭДМ, а нулями – их отсутствие. При этом направление потока мощности по отношению к полюсам упругого ЭДМ учитывается с помощью знаков: «–1» – мощность отводится, «1» – мощность подводится. Направление потока мощности определяется в зависимости от направления и величины источников внешних воздействий.
Матрица диссипативных ЭДМ формируется аналогично матрице упругих ЭДМ.
 Для фрикционных ЭДМ предусмотрены два типа матриц: фрикционов переключения и фрикционов ограничения. Фрикционы переключения представляют собой фрикционные элементы, расположенные между инерционными элементами (моделирование фрикционных муфт и тормозов в автомобильных трансмиссиях). Фрикцион ограничения располагается всегда между инерционным и упругим элементами динамической модели (моделирование сцепления колеса с дорогой). Матрица фрикционов переключения формируется аналогично матрице упругих ЭДМ с той разницей, что количество столбцов соответствует количеству фрикционов переключения. Матрица фрикционов ограничения представляет собой таблицу размерностью a´b, где a – число строк, равное количеству инерционных элементов, b – число столбцов, равное количеству упругих и диссипативных ЭДМ. При наличии фрикциона ограничения между i-м инерционным элементом и j-м упругим и (или) диссипативным ЭДМ элемент матрицы фрикционов ограничения принимается равным единице. Все остальные ее элементы будут иметь нулевые значения.
Для фрикционных ЭДМ предусмотрены два типа матриц: фрикционов переключения и фрикционов ограничения. Фрикционы переключения представляют собой фрикционные элементы, расположенные между инерционными элементами (моделирование фрикционных муфт и тормозов в автомобильных трансмиссиях). Фрикцион ограничения располагается всегда между инерционным и упругим элементами динамической модели (моделирование сцепления колеса с дорогой). Матрица фрикционов переключения формируется аналогично матрице упругих ЭДМ с той разницей, что количество столбцов соответствует количеству фрикционов переключения. Матрица фрикционов ограничения представляет собой таблицу размерностью a´b, где a – число строк, равное количеству инерционных элементов, b – число столбцов, равное количеству упругих и диссипативных ЭДМ. При наличии фрикциона ограничения между i-м инерционным элементом и j-м упругим и (или) диссипативным ЭДМ элемент матрицы фрикционов ограничения принимается равным единице. Все остальные ее элементы будут иметь нулевые значения.
Для трансформаторных ЭДМ, как и для фрик- ционных, предусмотрены матрицы трансформа- торных ЭДМ, расположенных между инерцион- ными элементами, и матрицы трансформаторных ЭДМ, расположенных между упругими и инерционными ЭДМ. Формирование матриц трансформаторных ЭДМ осуществляется по аналогии с матрицами фрикционных ЭДМ.
Заполнение матриц осуществляется в следующем порядке: инерционные элементы, внешние воздействия, фрикционные, трансформаторные, упругие, диссипативные элементы.
Правила построения динамических схем
Формирование динамической модели сложной механической системы необходимо осуществлять с учетом выполнения следующих правил построения:
· модель должна быть регулярной и без топологических вырождений [3];
· на динамической модели должны адекватно отображаться направления фазовых координат (направление передачи потока мощности);
· ЭДМ должны быть связаны друг с другом полюсами (не должно быть изолированных ЭДМ);
· необходимо соблюсти ограничения, накладываемые на взаимодействие полюсов некоторых типов ЭДМ;
· разветвление в динамической схеме может быть осуществлено только на полюсах упругих (диссипативных) и инерционных элементов, то есть для ЭДМ остальных групп полюс ЭДМ может быть соединен только один раз (может взаимодействовать только с одним ЭДМ).
Регулярность динамической модели подразумевает непосредственное взаимодействие инерционных элементов с безынерционными [3]. Кроме того, необходимо обеспечить отсутствие топологических вырождений в динамической модели, то есть наличие между инерционными элементами двух или более безынерционных элементов (упругих, диссипативных), относящихся к одной группе.
Направления фазовых координат определяются автоматически по направлению и величине источников внешних воздействий с учетом изменения знаков скоростей трансформаторными элементами. Направления фазовых координат совпадают с направлением передачи потока мощности.
В динамической модели не должно быть разрывов между ЭДМ (изолированных ЭДМ).
На полюсы некоторых ЭДМ накладываются ограничения при взаимодействии их между собой. Приложение источников потенциала может осуществляться только к инерционным элементам, а источников типа потока только к упругим и диссипативным ЭДМ. Элементы жестких планетарных рядов могут взаимодействовать только с инерционными ЭДМ. Полюсы фрикционных и трансформаторных элементов могут соединяться только с полюсами упругих (диссипативных) и инерционных ЭДМ.
Алгоритм автоматизированного формирования структуры динамических моделей в матричном виде
Рассмотрим особенности основных этапов алгоритма автоматизированного формирования динамических моделей, изображенного на рисунке 1.
Каждый ЭДМ имеет свой код, необходимый для идентификации типа элемента.
На 1-м этапе в соответствии со значением кода выбранного пользователем элемента определяются номер элемента путем добавления единицы к общему количеству элементов данного типа и координаты расположения.
Выполнение 2-го этапа начинается после размещения не менее двух ЭДМ. На этапах 2–5 устанавливаются связи между полюсами ЭДМ с учетом правил формирования динамических схем. Соблюдение правил формирования динамических схем проверяется сравнением типов ЭДМ, соединяемых линией.
Блоки 15, 16 служат для вывода сообщений о нарушениях, допущенных при построении линии связи, с описанием причины и неправильно указанных пользователем типов и номеров ЭДМ. Блоки 15 и 16 подразумевают обязательное редактирование динамической модели, то есть переход к блокам 2, 3 или 6.
После построения динамической схемы формируются матрицы инциденций по информации, содержащейся в соединительных линиях (блоки 7–13).
Рассмотрим пример построения динамической модели гидромеханической трансмиссии автомобиля БелАЗ-7555 (рис. 2) в прикладном ПО SMM_Model [2].
 На рисунке 2 использованы следующие обозначения моментов инерции: J1 – двигателя и насосного колеса гидротрансформатора, J2 – турбинного колеса гидротрансформатора, J3, J4 –ведущей и ведомой частей фрикционной муфты переключения соответственно, J5, J6 – ведущей и ведомой частей диапазонной фрикционной муфты соответственно, J7 – центрального редуктора главной передачи и дифференциала, J8 – колесных редукторов и шин ведущих колес (суммарный), J9 – автомобиля (суммарный); коэффициентов жесткости: с1, с2 – входного и промежуточного валов гидромеханической передачи соответственно, с3 – выходного вала гидромеханической передачи и карданного вала между коробкой передач и центральным редуктором главной передачи, с4 – полуосей (суммарный), а также с5 – суммарный коэффициент окружной жесткости шин ведущих колес; μi – коэффициенты демпфирования диссипативных элементов; uj, ηj – параметры трансформаторных элементов (передаточные числа и КПД); M1 – момент двигателя; M2, M3 – моменты сопротивления качению заднего и переднего мостов автомобиля; M4 – момент сопротивления воздуха и подъема автомобиля; Фk – фрикционные элементы управления; ГДТ – гидродинамический трансформатор.
На рисунке 2 использованы следующие обозначения моментов инерции: J1 – двигателя и насосного колеса гидротрансформатора, J2 – турбинного колеса гидротрансформатора, J3, J4 –ведущей и ведомой частей фрикционной муфты переключения соответственно, J5, J6 – ведущей и ведомой частей диапазонной фрикционной муфты соответственно, J7 – центрального редуктора главной передачи и дифференциала, J8 – колесных редукторов и шин ведущих колес (суммарный), J9 – автомобиля (суммарный); коэффициентов жесткости: с1, с2 – входного и промежуточного валов гидромеханической передачи соответственно, с3 – выходного вала гидромеханической передачи и карданного вала между коробкой передач и центральным редуктором главной передачи, с4 – полуосей (суммарный), а также с5 – суммарный коэффициент окружной жесткости шин ведущих колес; μi – коэффициенты демпфирования диссипативных элементов; uj, ηj – параметры трансформаторных элементов (передаточные числа и КПД); M1 – момент двигателя; M2, M3 – моменты сопротивления качению заднего и переднего мостов автомобиля; M4 – момент сопротивления воздуха и подъема автомобиля; Фk – фрикционные элементы управления; ГДТ – гидродинамический трансформатор.
Некоторые полученные матрицы, определяющие структуру динамической схемы, представлены в таблицах 1–5.
Таблица 1
Матрица инерционных элементов
|
Инерционные элементы
|
J1
|
J2
|
J3
|
J4
|
J5
|
J6
|
J7
|
J8
|
J9
|
|
J1
|
-1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J2
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J3
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J4
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
|
J5
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
|
J6
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
|
J7
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
|
J8
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
|
J9
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
Таблица 2
Матрица внешних воздействий, упругих и диссипативных элементов
|
Инерцион- ные элементы
|
Моменты воздействия
|
Упругие элементы
|
Диссипативные элементы
|
|
M1
|
M2
|
M3
|
M4
|
с1
|
с2
|
с3
|
с4
|
с5
|
μ1
|
μ2
|
μ3
|
μ4
|
μ5
|
|
J1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J2
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
|
J3
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
J4
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
|
J5
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
|
J6
|
0
|
0
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
0
|
0
|
-1
|
0
|
0
|
|
J7
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
-1
|
0
|
0
|
0
|
1
|
-1
|
0
|
|
J8
|
0
|
-1
|
0
|
0
|
0
|
0
|
0
|
1
|
-1
|
0
|
0
|
0
|
1
|
-1
|
|
J9
|
0
|
0
|
-1
|
-1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
Таблица 3
Матрица фрикционов ограничения
|
Инерционные элементы
|
Упругие элементы
|
Диссипативные элементы
|
|
с1
|
с2
|
с3
|
с4
|
с5
|
μ1
|
μ2
|
μ3
|
μ4
|
μ5
|
|
J1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J3
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J4
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J7
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J8
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J9
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
Таблица 4
Матрица фрикционов переключения и гидротрансформаторов
|
Инерционные элементы
|
Фрикционные элементы
|
ГДТ1
|
|
Ф1
|
Ф2
|
Ф3
|
|
J1
|
-1
|
0
|
0
|
-1
|
|
J2
|
1
|
0
|
0
|
1
|
|
J3
|
0
|
-1
|
0
|
0
|
|
J4
|
0
|
1
|
0
|
0
|
|
J5
|
0
|
0
|
-1
|
0
|
|
J6
|
0
|
0
|
1
|
0
|
|
J7
|
0
|
0
|
0
|
0
|
|
J8
|
0
|
0
|
0
|
0
|
|
J9
|
0
|
0
|
0
|
0
|
Таблица 5
Матрица трансформаторных элементов типа «зубчатая передача»
|
Инерционные элементы
|
Упругие элементы
|
Диссипативные элементы
|
|
с1
|
с2
|
с3
|
с4
|
с5
|
μ1
|
μ2
|
μ3
|
μ4
|
μ5
|
|
J1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J3
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
|
J4
|
0
|
2
|
0
|
0
|
0
|
0
|
2
|
0
|
0
|
0
|
|
J5
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
J6
|
0
|
0
|
3
|
0
|
0
|
0
|
0
|
3
|
0
|
0
|
|
J7
|
0
|
0
|
0
|
4
|
0
|
0
|
0
|
0
|
4
|
0
|
|
J8
|
0
|
0
|
0
|
5
|
0
|
0
|
0
|
0
|
5
|
0
|
|
J9
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Математическая модель, полученная на основе структурно-матричного метода моделирования [1], в символьном виде будет выглядеть следующим образом.

где ωi – угловые скорости сосредоточенных масс; Mн=f.(ω1, ω2) – момент на насосном колесе гидротрансформатора; Mт=f.(ω1, ω2) – момент на турбинном колесе гидротрансформатора; Ji – параметры инерционных элементов; Муj, Мдj – моменты в упругих и диссипативных элементах; Mфk – моменты на фрикционных муфтах; φi – углы поворота сосредоточенных масс.
Моменты в упругих элементах определяются по выражениям
 (2)
(2)
Моменты в диссипативных элементах вычисляются по уравнениям
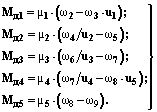 (3)
(3)
В качестве граничных условий для системы (1) выступают: минимальная (ωхх min) и максимальная (ωхх max) угловые скорости холостого хода двигателя (угловая скорость холостого хода двигателя зависит от положения педали акселератора γ и может принимать значение из интервала ωхх min≤ωхх≤ωхх max); момент двигателя, описываемый функцией M1=f(ωдвиг., γ); момент сцепления ведущих колес с дорогой, представленный в виде функции Mф4=f(φ), где φ – коэффициент сцепления ведущих колес с дорогой.
Преимущества предлагаемого алгоритма формирования структуры динамических моделей
Отличительными особенностями алгоритма являются простота и удобство.
Простота алгоритма заключается в том, что все связи ЭДМ должен указывать пользователь. Удобство состоит в том, что при указании пользователем полюсов ЭДМ, соединяемых между собой, осуществляется проверка правил формирования динамической схемы. Таким образом, в ПО SMM_Model исключена вероятность неправильного построения схем. Кроме того, предлагаемый алгоритм не требует от пользователя соблюдения правил очередности размещения ЭДМ. Они могут быть размещены на области построения динамических схем в любой последовательности независимо от типа.
Важным преимуществом алгоритма является возможность представления трансформаторных элементов сложной конфигурации (приемно-контрольных приборов и различного рода механических редукторов) в виде, близком к принципиальным или кинематическим схемам. Это достигается за счет специфической конфигурации соединительных линий и позволяет реализовывать графические образы сложной конфигурации.
Эффективность предлагаемого алгоритма заключается в его универсальности, он может использоваться для построения любой математической модели, состоящей из совокупности элементов, взаимодействующих между собой посредством соединительных линий.
В заключение можно сделать следующие выводы.
Разработанный алгоритм автоматизированного перехода от двухмерного графического представления структуры динамических моделей к матричной форме позволяет избежать соблюдения правил очередности размещения ЭДМ на поле, представить графический образ динамических схем в наиболее удобном для восприятия пользователем виде, осуществить контроль правильности построения динамических схем.
Предложенный алгоритм формирования матричного представления динамических моделей может быть применен и для автоматизации формирования структуры математических моделей в матричном виде с целью любого схемного представления технического объекта.
Разработанные алгоритм и методика автоматизированного формирования динамических моделей позволяют легко и просто осуществить построение динамической модели на дисплее монитора, приложение источников внешних воздействий (сил и вращающих моментов к сосредоточенным массам), редактирование динамических схем, описание нелинейных характеристик ЭДМ, представление структуры модели в матричной форме.
Литература
1. Тарасик В.П. Математическое моделирование технических систем: учебник для вузов. Минск: ДизайнПРО, 2004. 640 с.
2. Тарасик В.П., Евсеенко И.А. Прикладное программное обеспечение для моделирования объектов макроуровня // Автоматизация и современные технологии. 2007. № 4. С. 11–18.
3. Альгин В.Б. Динамика, надежность и ресурсное проектирование трансмиссий мобильных машин. Минск: Наука и техника, 1995. 256 с.






 (2)
(2)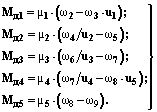 (3)
(3)