Беспроводные технологии передачи данных становятся все более популярными и востребованными в повседневной жизни, растут скорости и объемы передачи данных. Разработка нового оборудования в динамично изменяющихся условиях требует от инженеров специальных знаний и опыта, чтобы в максимально короткие сроки проектировать устройства со сбалансированными характеристиками. Это особенно актуально для ана- логовых микросхем. Кроме того, существует ряд обстоятельств, затрудняющих процесс проекти- рования. Во-первых, это отсутствие соответствующих аналитических моделей, описывающих аналоговые устройства на системном уровне. Во-вторых, большое количество вариантов устройств, различающихся по целевому назначению и, как следствие, по критериям оценки качества и, соответственно, по их топологии. При этом невозможно оценить функциональную зависимость между параметрами. И последнее, процесс проектирования трудоемок и требует больших временных затрат. Таким образом, поддержка принятия решений разработчиков на этапе проектирования и разработка соответствующих систем являются актуальной научно-технической задачей.
Коэволюционный подход
При проектировании любых микросхем необходимо обеспечить соответствие получаемых решений системе требований. Для задач оптимизации с векторным критерием и ограничениями, не обладающих удобными для оптимизации свойствами, необходимо применять соответствующие алгоритмы. Для решения многокритериальных задач оптимизации известно несколько схем: ранжирование частных критериев согласно их важности, выделение главного критерия и перевод остальных в ограничения, взвешенная сумма.
Эти подходы достаточно просты в применении и во многих случаях дают неплохие результаты. Тем не менее, они не защищены от субъективности, и их эффективность сильно зависит от назначения весовых коэффициентов, оценки важности частных критериев, выбор которых не всегда очевиден. К тому же, даже после много- кратных запусков алгоритма можно не получить репрезентативную аппроксимацию множества эффективных решений. Поэтому целесообразно использовать так называемые эволюционные алгоритмы, работающие одновременно со многими решениями и в результате позволяющие после одного запуска получать множество эффективных решений.
Для решения однокритериальных задач с ограничениями может быть применен коэволюционный генетический алгоритм, использующий метод множителей Лагранжа [1]. При таком подходе решение исходной задачи соответствует седловой точке функции Лагранжа. Преимуществами такого подхода являются его высокая эффективность при решении сложных задач оптимизации [2] и отсутствие необходимости настройки штрафных функций.
Этот же подход можно применить для решения задач оптимизации с векторным критерием, если вместо стандартного генетического алгоритма использовать его многокритериальную модификацию. Тогда процесс решения задачи будет представлять собой последовательное применение многокритериального генетического алгоритма к популяциям объектных переменных и коэффициентов Лагранжа.
Обобщенная схема предлагаемого подхода будет следующей.
1. Создать начальные популяции объектных переменных (А) и коэффициентов Лагранжа (В).
2. Оценить популяции A и B с использованием функции Лагранжа Li:
· A↔Li(X, Λ*)=fi(X)+∑Λ*×g(X), где i=1, …, K, j=1, …, M;
· B↔Li(X*,Λ)=fi(X*)+∑Λ×g(X*), где i=1, …, K, j=1, …, M.
3. Сгенерировать потомков, cmax запусков:
– сгенерировать потомков популяции A, amax запусков;
o MULTI GA1→ популяция A;
· оценить A: A↔Li(X, Λt*)=fi(X)+ +∑Λt*g(X);
– сгенерировать потомков популяции B, bmax запусков;
o MULTI GA2→ популяция B;
· оценить B: B↔Li(Xt*,Λ)=fi(Xt*)+ +∑Λg(Xt*).
– сохранить Парето-оптимальные (недоминируемые) решения.
4. Если выполнено условие останова, вывести полученные недоминируемые решения.
Здесь Х* и L* – случайные векторы объектных переменных и переменных Лагранжа из начальной популяции А и В соответственно; Хt* и Lt* – векторы объектных переменных и переменных Лагранжа на шаге t, которым соответствует максимальный ранг в архивном множестве недоминируемых решений.
Расчет значения пригодности индивидов из обеих популяций происходит с использованием функции Лагранжа, составленной для соответствующего критерия, при этом в качестве значений Xt* и Lt* устанавливаются выбранные значения соответствующей переменной из другой популяции.
 Результаты численных экспериментов [3] показывают высокую эффективность рассматриваемого подхода на различных типах многокритериальных задач оптимизации с целевыми функциями и ограничениями произвольного вида. Истинно паретовские решения среди предложенных алгоритмом недоминируемых точек составляют 90 % от всех генерируемых альтернатив. Оставшиеся 10 %, которые определены алгоритмом как недоминируемые, но на самом деле ими не являющиеся, расположены на незначительном удалении от множества Парето; расстояние до множества Парето варьируется в зависимости от задачи и обычно составляет 10–15 интервалов дискретизации в пространстве переменных. Репрезентативность аппроксимации множества эффективных решений несколько хуже в задачах со сложным рельефом целевых функций и ограничений, когда множество Парето несвязно, а ограничения не являются гладкими функциями. В таких случаях не наблюдается равномерного распределения решений во множестве Парето.
Результаты численных экспериментов [3] показывают высокую эффективность рассматриваемого подхода на различных типах многокритериальных задач оптимизации с целевыми функциями и ограничениями произвольного вида. Истинно паретовские решения среди предложенных алгоритмом недоминируемых точек составляют 90 % от всех генерируемых альтернатив. Оставшиеся 10 %, которые определены алгоритмом как недоминируемые, но на самом деле ими не являющиеся, расположены на незначительном удалении от множества Парето; расстояние до множества Парето варьируется в зависимости от задачи и обычно составляет 10–15 интервалов дискретизации в пространстве переменных. Репрезентативность аппроксимации множества эффективных решений несколько хуже в задачах со сложным рельефом целевых функций и ограничений, когда множество Парето несвязно, а ограничения не являются гладкими функциями. В таких случаях не наблюдается равномерного распределения решений во множестве Парето.
Усилитель сигналов с низким уровнем внутренних шумов
При проектировании аналоговых микросхем необходимо учесть ряд противоречивых требований к системе. Критерии могут варьироваться в зависимости от того, где эти устройства будут использоваться и какой тип сигналов будет проходить через них. Например, если усилитель работает с очень малыми сигналами (сразу после антенны или перед оптоэлектронным конвертером и в оптических коммуникационных системах), необходимо, чтобы он сам по себе добавлял настолько мало шума, насколько это возможно [4]. Такой усилитель называется усилителем с низким уровнем внутренних шумов и является одним из наиболее важных элементов в цепи каскадно-включенных устройств передачи радиосигнала. Коэффициент его шума оказывает наибольшее влияние на общий коэффициент шума микросхемы.
Например, общий коэффициент шума каскада из n ступеней таков:  , где Fi – коэффициент шумов i-го усилителя; Gi – коэффициент усиления i-го усилителя [4].
, где Fi – коэффициент шумов i-го усилителя; Gi – коэффициент усиления i-го усилителя [4].
Это известное уравнение Фрииса, которое утверждает, что в цепи приемника общий коэффициент шума приблизительно равен коэффициенту шума первой ступени в том случае, если она обладает достаточным коэффициентом усиления, что является важным наблюдением для проектирования малошумящих усилителей.
В связи с тем, что общее количество элементов в схеме достаточно велико, процесс создания адекватной аналитической модели может быть более ресурсоемким, чем сам процесс проектирования. Поэтому в исследованиях авторов модель была реализована в виде черного ящика с помощью симулятора Advanced Design software [5]. При расчете производительности используется полный перечень паразитных эффектов, которые присутствуют в реальных устройствах.
Эквивалентная схема усилителя представлена на рисунке 1.
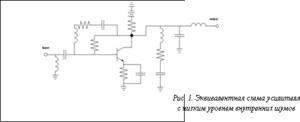 Общее количество смешанных переменных равно четырнадцати. Кроме того, есть два критерия и три ограничения: рабочая частота устройства FR=2 GHz, напряжение постоянного тока равно 3 V; коэффициент усиления Power Gain: G=11 dB ± 1, то есть |Gi-11|≤1; входные и выходные коэффициенты отражения |Гin,i|, |Гout,i|≤0,1; коэффициент шума NFi→min и потребление постоянного тока PDC,i→min.
Общее количество смешанных переменных равно четырнадцати. Кроме того, есть два критерия и три ограничения: рабочая частота устройства FR=2 GHz, напряжение постоянного тока равно 3 V; коэффициент усиления Power Gain: G=11 dB ± 1, то есть |Gi-11|≤1; входные и выходные коэффициенты отражения |Гin,i|, |Гout,i|≤0,1; коэффициент шума NFi→min и потребление постоянного тока PDC,i→min.
Характеристики оригинальной схемы усилителя на рисунке 2 представлены в виде окружности. Как видно, значения ее параметров, выбранные с помощью модуля оптимизации в програм- мном продукте ADS, не обеспечивают функционирование микросхемы в желаемом диапазоне измеряемых характеристик. Коэффициенты отражения не удовлетворяют заданным характеристикам.
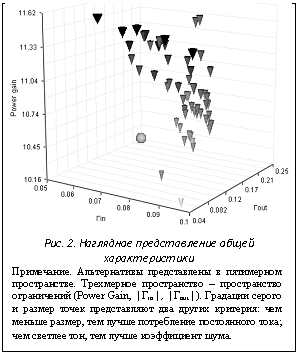 Результаты решения задачи коэволюционным алгоритмом представлены в виде треугольников (рис. 2). Все 50 альтернативных решений задачи имеют меньшее потребление постоянного тока, меньший коэффициент шума, при этом коэффициенты усиления и отражения находятся в допустимом диапазоне. Таким образом, альтернативные решения являются Парето-оптимальными, что в дальнейшем значительно облегчает решение задачи проектирования. На рисунке 2 показано, что наилучшая альтернатива будет соответствовать самой светлой, самой маленькой фигуре в допустимой области.
Результаты решения задачи коэволюционным алгоритмом представлены в виде треугольников (рис. 2). Все 50 альтернативных решений задачи имеют меньшее потребление постоянного тока, меньший коэффициент шума, при этом коэффициенты усиления и отражения находятся в допустимом диапазоне. Таким образом, альтернативные решения являются Парето-оптимальными, что в дальнейшем значительно облегчает решение задачи проектирования. На рисунке 2 показано, что наилучшая альтернатива будет соответствовать самой светлой, самой маленькой фигуре в допустимой области.
В заключение следует отметить, что в работе предложен, исследован на тестовых задачах и применен для решения реальной практической задачи новый метод условной многокритериальной оптимизации. Алгоритм, разработанный на основе этого метода, эффективен при решении как многокритериальных задач со сложными целевыми функциями, так и сложных практических задач, его также можно применять в составе систем поддержки принятия решений. С помощью разработанной системы поддержки проектных решений проведен выбор эффективных параметров усилителя с низким уровнем шумов, который обладает оптимальными свойствами по двум критериям и соответствует предъявленным требованиям. Применяемая модель, построенная на основе ПО от мирового лидера в области электронных систем Agilent Software, предоставляет пользователю все возможности для инженерного проектирования и, таким образом, позволяет автоматизировать многие этапы проектирования, в том числе и выбор конфигурации.
Литература
1. Barbosa H.J.C. A genetic algorithm for min-max problems // E. Goodman et al (Eds). Proceedings of the First International Conference on Evolutionary Computation and Its Applications (EvCA'96). M.: IHPCS of RAS, 1996, pp. 99–109.
2. Процыков Г.В., Семенкин Е.С., Токмин К.А. Об эффективности коэволюционного подхода в практических задачах оптимизации // Вестн. Красноярск. гос. ун-та: Сер. Физико-математические науки. 2005. № 4. С. 233–239.
3. Семенкин Е.С., Токмин К.А. Коэволюционный подход для решения задач условной многокритериальной оптимизации // Вестн. Сибир. гос. аэрокосмич. ун-та им. акад. М.Ф. Решетнева. 2008. № 4 (21). С. 47–51.
4. Prasad S., Schumacher H., Gopinath A. High-Speed Electronics and Optoelectronics: Devices and Circuits // Cambridge University Press, Cambridge, UK 2009.
5. Advanced Design System (ADS). URL: http://www.home.agilent.com/agilent/product.jspx?nid=-34346.0 (дата обращения: 21.03.2011).



 Результаты численных экспериментов [3] показывают высокую эффективность рассматриваемого подхода на различных типах многокритериальных задач оптимизации с целевыми функциями и ограничениями произвольного вида. Истинно паретовские решения среди предложенных алгоритмом недоминируемых точек составляют 90 % от всех генерируемых альтернатив. Оставшиеся 10 %, которые определены алгоритмом как недоминируемые, но на самом деле ими не являющиеся, расположены на незначительном удалении от множества Парето; расстояние до множества Парето варьируется в зависимости от задачи и обычно составляет 10–15 интервалов дискретизации в пространстве переменных. Репрезентативность аппроксимации множества эффективных решений несколько хуже в задачах со сложным рельефом целевых функций и ограничений, когда множество Парето несвязно, а ограничения не являются гладкими функциями. В таких случаях не наблюдается равномерного распределения решений во множестве Парето.
Результаты численных экспериментов [3] показывают высокую эффективность рассматриваемого подхода на различных типах многокритериальных задач оптимизации с целевыми функциями и ограничениями произвольного вида. Истинно паретовские решения среди предложенных алгоритмом недоминируемых точек составляют 90 % от всех генерируемых альтернатив. Оставшиеся 10 %, которые определены алгоритмом как недоминируемые, но на самом деле ими не являющиеся, расположены на незначительном удалении от множества Парето; расстояние до множества Парето варьируется в зависимости от задачи и обычно составляет 10–15 интервалов дискретизации в пространстве переменных. Репрезентативность аппроксимации множества эффективных решений несколько хуже в задачах со сложным рельефом целевых функций и ограничений, когда множество Парето несвязно, а ограничения не являются гладкими функциями. В таких случаях не наблюдается равномерного распределения решений во множестве Парето. , где Fi – коэффициент шумов i-го усилителя; Gi – коэффициент усиления i-го усилителя [4].
, где Fi – коэффициент шумов i-го усилителя; Gi – коэффициент усиления i-го усилителя [4].
 Результаты решения задачи коэволюционным алгоритмом представлены в виде треугольников (рис. 2). Все 50 альтернативных решений задачи имеют меньшее потребление постоянного тока, меньший коэффициент шума, при этом коэффициенты усиления и отражения находятся в допустимом диапазоне. Таким образом, альтернативные решения являются Парето-оптимальными, что в дальнейшем значительно облегчает решение задачи проектирования. На рисунке 2 показано, что наилучшая альтернатива будет соответствовать самой светлой, самой маленькой фигуре в допустимой области.
Результаты решения задачи коэволюционным алгоритмом представлены в виде треугольников (рис. 2). Все 50 альтернативных решений задачи имеют меньшее потребление постоянного тока, меньший коэффициент шума, при этом коэффициенты усиления и отражения находятся в допустимом диапазоне. Таким образом, альтернативные решения являются Парето-оптимальными, что в дальнейшем значительно облегчает решение задачи проектирования. На рисунке 2 показано, что наилучшая альтернатива будет соответствовать самой светлой, самой маленькой фигуре в допустимой области.