Известно, что система дедуктивного вывода в общем случае недетерминирована, и поэтому проблема управления поиском вывода актуальна для построения решателей проблем. При выводе наблюдается экспоненциальный рост затрат на обработку огромного пространства поиска при решении задач практической сложности, а именно, увеличение объема хранимой информации и времени решения задачи. Одним из путей решения этой проблемы является параллелизм, который может быть реализован как мультипоиск и распределенный поиск [1, 2]. Стратегии мультипоиска приписывают каждому параллельному процессу свой план поиска, в то время как стратегии распределенного поиска выдают каждому параллельному процессу свою порцию пространства поиска. Эти два подхода не являются взаимоисключающими, между ними имеется связь.
Говоря о стратегии поиска, прежде всего следует упомянуть о стратегиях, основанных на упорядочении (ordering-based strategies). Необходимо отметить, что среди них имеются стратегии, ориентированные как на расширение множества дизъюнктов для метода резолюции, так и на его сокращение путем поглощения. Упорядочение здесь понимается как наличие обоснованного порядка выражений, подлежащих процедуре поиска вывода. Стратегии, основанные на упорядочении, используют поиск только наилучшего (с применением эвристик) и, как правило, не очень восприимчивы к разрешению целей. Однако использование в них семантических (например в семантической резолюции) или поддерживающих (например в резолюции множества поддержки) требований настраивает поиск на разрешение целей. Стратегии, основанные на упорядочении, являются синтетическими, получаемыми образованием одних цепочек вывода из других.
Иной тип стратегий – стратегия редукции подцелей, реализованная в аналитических таблицах. Уже из названия ясно, что вычисление цели состоит в редукции ее подцелей и последующем их разрешении. Если в подходе, который основан на упорядочении, стратегии ограничивают поиск наложением локальных требований на каждый шаг вывода, то стратегии редукции подцелей ограничивают поиск наложением требований на саму форму вывода. Так, в методе аналитических таблиц происходит разложение формулы на подформулы и ищется их невыполнимость, как в методах опровержения. Эти стратегии по сути являются аналитическими.
Главное внимание в статье уделено параллелизму на уровне распределенного поиска. Ключевой фактор в классификации методов с параллельным поиском заключается в дифференциации и комбинировании активности дедуктивных процессов. Принцип разделения пространства поиска на ряд подпространств положен в основу распределенного поиска, в котором существенную роль играет организация связи между порциями пространства.
Рассматриваемый авторами метод аналитических таблиц имеет одну и ту же систему вывода (так называемую гомогенную систему) и осуществляет параллелизм на уровне распределенного поиска.
Метод аналитических таблиц
Настоящий метод является эффективной процедурой доказательства теорем и для логики высказываний, и для логики предикатов первого порядка. Как и метод резолюции, он относится к методам опровержения, то есть когда для доказательства общезначимости формулы A доказывается ее противоречие (¬A) [2, 3]. Но если метод резолюции работает с формулами, представленными в конъюнктивной нормальной форме, то метод аналитических таблиц оперирует формулами в дизъюнктивной нормальной форме. Вывод осу- ществляется на бинарных деревьях, вершины которых отмечены формулами, причем вершина называется концевой, если не имеет потомков, простой, если у нее только один потомок, и дизъюнктивной, если два потомка. Каждая ветвь дерева представлена конъюнкцией формул, а само дерево – дизъюнкцией своих ветвей.
Известно, что в методе аналитических таблиц четыре правила вывода, два из которых относятся к логике высказываний (α, β), а два – к логике предикатов первого порядка (γ, δ) [2, 3].
Правило α: если формула Х есть α, то к дереву надо добавить вершину, отмеченную формулой α1, и затем на этой же ветви другую вершину, отмеченную α2:  , где α – формула конъюнктивного типа, состоящая из компонент α1 и α2.
, где α – формула конъюнктивного типа, состоящая из компонент α1 и α2.
Правило β: если формула Х есть β, надо расщепить идущую от вершины β ветвь на две ветви, вершину на левой ветви отметить формулой β1, а на другой – β2: 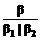 , где β – формула дизъюнктивного типа, состоящая из компонент β1 и β2.
, где β – формула дизъюнктивного типа, состоящая из компонент β1 и β2.
Правило δ: если формула X есть δ, то к дереву надо добавить вершину, отмеченную формулой δ(с). Это означает, что к формуле Х применена подстановка с вместо всех вхождений переменной x в X: 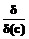 , где δ – формула экзистенционального типа, имеющая кванторы $ или Ø", c – новый параметр, не входящий в исходную формулу, чья невыполнимость доказывается.
, где δ – формула экзистенционального типа, имеющая кванторы $ или Ø", c – новый параметр, не входящий в исходную формулу, чья невыполнимость доказывается.
Правило γ: если формула X есть γ, то к дереву надо добавить вершину, отмеченную формулой γ(a). Это означает, что к формуле Х применена подстановка а вместо всех вхождений переменной x в X: 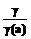 , где γ – формула универсального типа, имеющая кванторы " или Ø$, a – любой параметр.
, где γ – формула универсального типа, имеющая кванторы " или Ø$, a – любой параметр.
Назовем правила α, β, γ, δ правилами расширения таблицы. Доказано, что метод аналитических таблиц обладает непротиворечивостью, то есть этим методом невозможно доказать формулу и ее отрицание одновременно. Кроме того, метод полон, то есть, если формула Х общезначима, то она доказуема (выводима) методом аналитических таблиц [3, 4].
В общем случае правила расширения таблицы недетерминированы. Но в отличие от пропозиционального случая в логике предикатов возможно многократное (в худшем случае бесконечное) повторение правил расширения таблицы без получения замкнутого дерева, хотя оно может существовать. Источником такой трудности является γ-правило. Если правила α, β, δ применяются к формуле X только один раз, то в случае с γ-правилом это не так. Предположим, например, что формула "x1, …, xn F(x1, …, xn) содержит m констант. Тогда потребуется добавить mn различных замкнутых предложений к пути в таблице (функциональные символы в подстановке отсутствуют), то есть количество формул, которое нужно добавить, возрастает экспоненциально в зависимости от количества кванторов.
Для уменьшения недетерминированности выбора правил сначала используем все α- и δ-правила (нет ветвления). Затем применим β-правила и только после этого γ-правила.
Назовем таблицу атомарно замкнутой, если каждая ветвь дерева содержит некоторую атомарную формулу и ее отрицание (то есть контрарную пару P и ØP). Таким образом, если формула Х общезначима или ØX невыполнима, то существует атомарно замкнутая таблица для Х.
Метод фиктивных переменных
Для избежания комбинаторных проблем, вызванных многократным добавлением к пути экземпляров универсальных формул, рассмотрим предложенный Р. Джонсоном метод фиктивных переменных [4].
Вместо квантифицированных переменных, входящих в формулы, вводятся фиктивные переменные. Их можно заменить любым именем (константой), если соблюсти определенные ограничения.
Обозначим фиктивные переменные как dx или dx, где х – положительное целое число.
Введем несколько определений.
Определение 1 (Редукция). Редукция – упорядоченная пара вида , где d – переменная, t – терм. Это означает, что t будет подставлен вместо фиктивной переменной d в любое множество термов или формул, к которым подстановка применима.
Определение 2 (Подстановка). Подстановка – конечная последовательность редукций (множество редукций).
Необходимо различать два вида редукций : константная, где t – константа, и фиктивная, где t – фиктивная переменная. Очевидно, что подстановка – это конечная последовательность редукций, а унификация определяется обычным образом: если имеются термы t и v, содержащие переменные, то подстановка σ, такая, что tσ=vσ, называется унификатором для t и v.
Подстановка σ={, …, } называется идемпотентной, если для 1≤i,j≤n xi не входит в ti, поэтому переменные в идемпотентной подстановке не появляются одновременно на левой и правой сторонах любой редукции или различных редукций [4, 5]. Естественно, что интерес представляют только непротиворечивые идемпотентные подстановки (НИП). Следовательно, всякий раз, когда в результате композиции получает- ся противоречивая подстановка θ, где , Îθ, a и b – константы и a≠b, θ будет исключена.
Метод фиктивных переменных во многом похож на метод Фиттинга, оперирующий свободными переменными [6]. Он отличается от метода полного перебора способами работы с универсальными формулами. Если метод полного перебора добавляет новую копию формулы для каждой новой константы, которая появляется на пути, метод фиктивных переменных просто помещает фиктивную переменную на место всех вхождений универсально квантифицированной переменной, то есть вместо фиктивной переменной может быть подставлена любая константа, находящаяся на пути. Эта подстановка может создать контрарную пару и тем самым замкнуть путь. Если при последовательном конструировании таблицы не возникает никаких проблем, то в параллельном случае необходимо поддерживать непротиворечивые подстановки для фиктивных переменных, которые возникают более чем на одном пути.
Опишем схему, позволяющую справиться с этой проблемой [4].
Имеем формулу F и подстановку σ={, , …, }, Fσ – результат применения каждой редукции {} к F для 0≤p≤n-1, то есть в F каждое вхождение xp заменяется на tp.
Унификация формул или множества формул подразумевает унификацию соответствующих термов в формулах. Например, рассмотрим формулы F(a, x)→G(x) и F(y, b)→G(b), где x и y – фиктивные переменные. Эти формулы унифицируются подстановкой {, }. Рассмотрим ограниченное множество подстановок. Если любая переменная xp входит в левую часть константной редукции в σ, это будет ее единственным вхождением в σ. Данное обстоятельство гарантирует, что xp может быть связана только единственной константой, σ также не содержит тождественных редукций, то есть редукций вида . Если есть подстановки вида σ={} и θ={}, то σθ={, }. Однако σ={} является двунаправленной, так, если θ={}, тогда σθ={, } дает такой же результат. Будем ссылаться на этот процесс как на внесение констант.
В данном случае представляют интерес только константные подстановки, за исключением случая, где одна переменная связана с другой, но ни одна из них, в свою очередь, не связана с константой. Получается, что порядок применения редукций не важен.
Параллелизм в методе фиктивных переменных
Опишем метод, который параллельно пытается построить подстановки, способные замкнуть таблицу. Отметим, что в таблице могут существовать пути, не требующие унификации, то есть когда контрарная пара F и ØF не нуждается в унификации. Если на пути существуют две формулы, замыкающие его без унификации, это называется константным замыканием. Однако, если на пути присутствуют формулы типов F(a, x) и ØF(y, b), где a и b – константы, x и y – фиктивные переменные, то их необходимо унифицировать, то есть применить к ним подстановку {, } и получить контрарную пару F(a, b) и ØF(a, b).
Главная проблема, на которую нужно обратить внимание в параллельном случае, состоит в поддержании непротиворечивости подстановок, так как многие фиктивные переменные разделяются между нитями и могут связываться с различными константами, что недопустимо.
Как было отмечено, две или более редукций являются противоречивыми, если пытаются связать одну и ту же фиктивную переменную с различными константами. Противоречивая подстановка – это подстановка, содержащая одну или более пар противоречивых редукций. Рассмотрим пути Р1 и Р2 таблицы Т, где путь Р1 может быть замкнут после унификации формул F(a, x) и ØF(y, b), а путь Р2 – после унификации формул G(a, x) и ØG(y, c).
Путь Р1 требует подстановки {, } для замыкания, в то время как Р2 требует {, }. Очевидно, что эти подстановки противоречивы, поэтому замыкание путей с ними несостоятельно и невозможно.
Введем еще несколько определений [4].
Определение 3 (П-множество). Возможное унифицирующее множество П (П-множество) для подтаблицы Т′ таблицы Т содержит редукции, требующиеся для замыкания всех путей в Т′. Каждое П-множество состоит из непротиворечивых идемпотентных подстановок.
Отметим, что Т′ может быть частью таблицы Т, всей таблицей Т или только единственным путем.
Определение 4 (N-множество). Необходимое унифицирующее множество N (N-множество) является множеством из П-множеств.
N-множество содержит полное множество всех возможных подстановок, которые позволяют таблице замкнуться. Если какой-либо путь не может быть замкнут без унифицирования термов, необходимо наличие у него, по крайней мере, одной подстановки, унифицирующей рассматриваемые термы.
N- и П-множества будут описаны следующим образом: N={П0, …, Пn}, где n≥0, N – N-множество, П – П-множество.
Отметим, что N-множество – это множество, состоящее из П-множеств, в то время как П-множество – это множество, состоящее из редукций: П={, …, }, где p≥0, di≠dj и di≠tj (i≠j, 0≤i, j≤p). П-множество – это подстановка, которая унифицирует соответствующие аргументы x1, …, xn и y1, …, yn для двух формул, делая их контрарными.
У всякого N- и П-множества есть соответствующая таблица или подтаблица Т.
Применяя П к формулам на каждом пути в Т, получаем контрарную пару формул, замыкая Т. Аналогично применение любого из П-множеств в N замыкает Т. В итоге получаем замкнутую таблицу Т.
Опишем некоторые свойства подстановок и выполняемых над ними операций.
Определение 5 (Композиция). Если σ и θ – две подстановки, то их композиция σθ является подстановкой, определяемой как (Fσ)θ=F(σθ) для всех формул F.
Определение 6 (Допустимость). Даны две подстановки σ1 и σ2, их композиция θ=σ1σ2 допустима тогда и только тогда, когда для любой формулы F Fσ1σ2=Fσ2σ1 (то есть θ коммутативна) и все редукции в θ непротиворечивы.
Результатом допустимой композиции является НИП. Необходимо гарантировать, что в итоге композиции будет получена НИП. Для этого к допустимой композиции θ следует применить операцию внесения констант. Такая операция, примененная к редукции, замещает редукции вида ={, } на две редукции вида ={, }.
Введем два понятия непротиворечивости.
Определение 7 (Сильно непротиворечивы). Две подстановки σ и θ сильно непротиворечивы, если σÍθ.
Определение 8 (Слабо непротиворечивы). Две подстановки σ и θ слабо непротиворечивы, если Îσ, Îθ, a≠b и a или b – переменные.
Сильная и слабая непротиворечивости составляют условия, которые проверяются при построении подстановок в композициях. Если замыкающие подстановки для всех путей в таблице сильно непротиворечивы, таблица замыкается немедленно. Если замыкающие подстановки слабо непротиворечивы, тогда таблица все еще может быть замкнута, однако необходимо выполнить композицию замыкающих подстановок, чтобы проверить наличие в них скрытых противоречий. Рассмотрим случай, когда три пути замыкаются с подстановками: σ={}, γ={} и λ={}. Композиция (σγ)λ дает противоречивую подстановку, содержащую редукции и . Однако, если γ={}, композиция будет непротиворечивой.
Любое N-множество содержит множество П-множеств, каждое из которых унифицирует по крайней мере одну пару контрарных формул на всех путях конкретной таблицы. Операция согласования объединяет N-множества N1 и N2, соответствующие паре таблиц, выводя единственное N-множество, содержащее П-множества, которые замыкают обе таблицы. Унификация N-множеств называется согласованием [4, 5].
Определение 9 (Наиболее общий унификатор). Говорят, что подстановка θ, унифицирующая формулы F1 и F2, называется наиболее общим унификаторам (НОУ), если для всех унификаторов σ формул F1 и F2 существует такая подстановка γ, что σ=θγ.
Рассмотрим формулы F1(x, b, z) и F2(a, y, c). Они могут быть унифицированы подстановкой θ={, , }. Здесь θ – НОУ для этих формул, так как не существует такой подстановки γσ, что F1(x, b, z)γ=F2(a, y, c)γ, и θ=γσ, где σ≠∅. Когда N-множество сгенерировано в концевой вершине, каждое П-множество в N-множестве составляет НОУ для пары контрарных формул на этом пути.
Определение 10 (Наиболее общая подстановка). Если дано множество подстановок θ={θ1, …, θn}, то θi (i=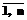 ) – наиболее общая подстановка (НОП) в θ, если не существует никакой θjÎθ, где θi – экземпляр для θj. Заметим, что может быть больше одной НОП в θ. N-множество является множеством НОУ. Каждый НОУ множества термов является НОП, которая унифицирует множество.
) – наиболее общая подстановка (НОП) в θ, если не существует никакой θjÎθ, где θi – экземпляр для θj. Заметим, что может быть больше одной НОП в θ. N-множество является множеством НОУ. Каждый НОУ множества термов является НОП, которая унифицирует множество.
Авторы стремятся составить множества подстановок, поддерживая непротиворечивость каждого составленного П-множества и гарантируя, что результирующее N-множество N не содержит П-множество, которое менее общее (то есть является экземпляром), чем любое другое П-множество в N. Поэтому каждое N-множество содержит множество НОП, и результат согласования двух N-множеств является либо Æ, либо множеством НОП. Операция согласования пытается получить множество НОП для контрарных формул на всех путях таблицы, соответствующих согласованной паре N-множеств. Однако может быть более одного множества, замыкающего каждый путь, поэтому N-множество может содержать более одного П-множества.
Процесс согласования N-множеств требует создания всех перестановок пар П-множеств из двух N-множеств (по одному П-множеству из каждого N-множества). Затем любое из результирующих П-множеств, которое содержит несогласованные подстановки или экземпляры каких-либо П-множеств из того же самого N-множества, исключаются из этого множества. Несогласованные редукции – результат возникновения конфликтов при присвоении фиктивным переменным значений, то есть одна и та же переменная унифицируется с разными константами при замыкании таблицы. Для поддержки полноты замыкания сначала включаются все возможные подстановки, часть которых при обнаружении противоречий позже будет исключена. Очевидно, что П-множество всегда будет непустым, поскольку пустая подстановка говорит, что замыкание пути происходит без подстановки.
Определение 11 (Согласование). Согласование N1ÅN2 двух N-множеств N1 и N2 – это множество, полученное композицией всех пар П-множеств, входящих в N1 и N2. N1ÅN2 также является N-множеством [4].
Множество N0 получается из согласования N-множеств N1 и N2. N1 – множество подстановок, каждая из которых вызывает замыкание всех ветвей левой части таблицы (антецедента), находящейся ниже ветвления. Аналогично N2 – множество подстановок, которое замыкает все ветви в правой части таблицы (консеквента), находящейся ниже ветвления. Таким образам, согласование двух N-множеств N1={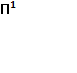 , ...,
, ..., } и N2={
} и N2={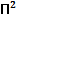 , ...,
, ..., } состоит в композиции каждого члена N1 с каждым членом N2. Это потребует создания n подстановок, где n=j*k (j – количество П-множеств в N1, k – количество П-множеств в N2). Для сокращения числа подстановок N0 следует исключить все конфликтующие подстановки и те, которые являются экземплярами других членов N0 (то есть не являются НОУ в N0).
} состоит в композиции каждого члена N1 с каждым членом N2. Это потребует создания n подстановок, где n=j*k (j – количество П-множеств в N1, k – количество П-множеств в N2). Для сокращения числа подстановок N0 следует исключить все конфликтующие подстановки и те, которые являются экземплярами других членов N0 (то есть не являются НОУ в N0).
Корневое N-множество – это N-множество, полученное согласованием N-множеств наибольшей пары частей таблицы (то есть парой, непосредственно находящейся ниже самого верхнего ветвления). Каждое П-множество в корневом N-множестве является НОУ для таблицы, которое приведет к замыканию каждого пути таблицы.
Метод фиктивных переменных для аналитических таблиц полон и непротиворечив, что доказывается соответствующими теоремами [4, 6]. Проиллюстрируем параллельный метод аналитических таблиц с фиктивными переменными (см. рис.).
Прокомментируем полученное решение. Первые 14 шагов проходят в соответствии с последовательным алгоритмом метода аналитических таблиц с фиктивными переменными. В универсальных формулах с кванторами ∀x или ¬∃x осуществляются подстановки фиктивных переменных вместо x, y и z, то есть x=d1, x=d2, x=d3, y=d4 и z=d5. Затем в экзистенциональных формулах с кванторами ∃x или ¬∀x реализуются подстановки констант вместо переменных, то есть y=a (для F(d1, y)), y=b (для G(d2, y)) и x=c (для H(x, y)).
После этого идет разветвление. Применение результатов композиции подстановок дает следующее:
{{F(d1, a), ¬F(d3, a)}, {G(d2, b), ¬G(d3, b)}}.
Отсюда N1={{}, {}}.
В отличие от левого пути правый еще раз разветвляется. Имеем:
{{F(d1,a), ¬F(a,d5)}, {G(d2,b), ¬G(b,d5)}},
N2={{, }, {, }}.
{{¬H(c,d4), H(d3,d5) }},
N3={{, }}.
Применяем операцию согласования, которая объединяет N2 и N3, получая N-множество N4:
N4={{, }, {, }} ⨁ ⨁ {{, }}.
Процесс согласования N-множеств, как уже упоминалось, требует создания всех перестановок пар П-множеств из двух N-множеств, причем несогласованные подстановки или экземпляры любых П-множеств из одного и того же N-множества будут исключены:
N4={{, }, {, }}È È{{, }, {, }}={{, , , }, {, , , }}.
Выполняем согласование между левой и правой ветвями:
N1={{}, {}};
N4={{, , , },
{, , , }}.
N1⨁N4={{}, {, , , }} È{{}, {, , , }} È {{}, {, , , }} È {{}, {, , , }} = {{, , , , } {, , , , }, {, , , , } {, , , , }}.
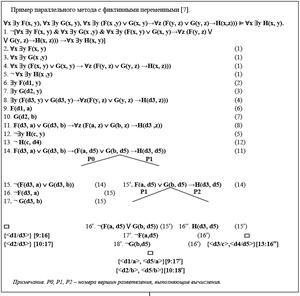 В итоговом согласовании первое и четвертое N-множества являются противоречивыми (выделено подчеркиванием), поэтому их следует исключить.
В итоговом согласовании первое и четвертое N-множества являются противоречивыми (выделено подчеркиванием), поэтому их следует исключить.
Nитог={{, , , , }, {, , , , }}.
В заключение отметим, что авторами рассмотрены основные методы вывода на аналитических таблицах для логики предикатов первого порядка. Исследованы различные способы повышения эффективности вывода и возможности по внесению в него параллелизма. Разработан метод параллельного вывода с фиктивными переменными, который показал свою эффективность в задачах практической сложности. В дальнейшем для повышения эффективности предполагается введение эвристик. Одной из таких эвристик при поиске в глубину может быть исследование только левосторонней ветви, в то время как правосторонняя сохраняется при выполнении ее расширения позже. Это позволит уменьшить затраты памяти на хранение формул.
Литература
1. Bonacina M.P. A Taxonomy of Parallel Strategies for Deduction // Ann. Of Math. and Artificial Intell. 2000. 29 (1–4), pp. 223–257.
2. Вагин В.Н. [и др.]. Достоверный и правдоподобный вывод в интеллектуальных системах; [под ред. В.Н. Вагина, Д.А. Поспелова]. М.: Физматлит, 2008. 712 с.
3. Smullan R.V. First-order logic/ Springer-Verlag, Berlin, Heidelberg, New York, 1968. 158 p.
4. Robert Johnson. Parallel Analytic Tableaux Systems, Submitted for the degree of Doctor of Philosophy, 1996. 372 p.
5. Wolfgang Bibel. Automated Theorem Proving, 2nd Ed. Vieweg, 1987.
6. Melvin Fitting. First-Order Logic and Automated Theorem Proving. N.Y.: Springer-Verlag, 1990. 511 p.
7. Francis Jeffry Pellertier. Seventy-Five Problems for Testing Automatic Theorem Provers // Journal of Automated Reasoning. 1986. № 2, pp. 191–216.



 , где α – формула конъюнктивного типа, состоящая из компонент α1 и α2.
, где α – формула конъюнктивного типа, состоящая из компонент α1 и α2.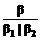 , где β – формула дизъюнктивного типа, состоящая из компонент β1 и β2.
, где β – формула дизъюнктивного типа, состоящая из компонент β1 и β2.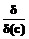 , где δ – формула экзистенционального типа, имеющая кванторы $ или Ø", c – новый параметр, не входящий в исходную формулу, чья невыполнимость доказывается.
, где δ – формула экзистенционального типа, имеющая кванторы $ или Ø", c – новый параметр, не входящий в исходную формулу, чья невыполнимость доказывается.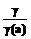 , где γ – формула универсального типа, имеющая кванторы " или Ø$, a – любой параметр.
, где γ – формула универсального типа, имеющая кванторы " или Ø$, a – любой параметр. ) – наиболее общая подстановка (НОП) в θ, если не существует никакой θjÎθ, где θi – экземпляр для θj. Заметим, что может быть больше одной НОП в θ. N-множество является множеством НОУ. Каждый НОУ множества термов является НОП, которая унифицирует множество.
) – наиболее общая подстановка (НОП) в θ, если не существует никакой θjÎθ, где θi – экземпляр для θj. Заметим, что может быть больше одной НОП в θ. N-множество является множеством НОУ. Каждый НОУ множества термов является НОП, которая унифицирует множество. , ...,
, ..., } и N2={
} и N2={ , ...,
, ...,
