Совершенствование существующих и создание новых технологий тесно связаны с разработкой их математических моделей. Особую роль при этом играют модели физико-химических процес- сов (ФХП), описывающих изменения химического состава и структуры вещества. Они широко используются при разработке процессов в химической и нефтегазовой промышленности, микроэлектронике, в материаловедении и т.д. Отличительной особенностью данных технологий является наличие широкого круга химических компонентов и параллельно протекающих ФХП как в объеме, так и на поверхности раздела фаз [1].
В связи с этим одной из ключевых задач, возникающих при построении указанных моделей, является выбор их структуры, то есть совокупности учитываемых химических компонентов, ФХП и взаимосвязей между ними.
Для принятия решения о целесообразности включения того или иного ФХП или компонента в модель ее разработчику необходимо иметь возможность быстро оценить степень влияния данных факторов на целевые показатели описываемого процесса. Удачным решением указанной проблемы может быть создание такого комплексного математического подхода, который позволял бы быстро строить модель процесса из готовых модулей, описывающих ФХП и компоненты.
 В качестве такого подхода к комплексному моделированию ФХП автором статьи разработан новый вариант метода вероятностного клеточного автомата (ВКА) [1–3]. В данном варианте метода моделируемый объект рассматривается на микроскопическом уровне. Атомно-молекулярной структуре объекта ставится в соответствие сетка ячеек ВКА, состояния которых определяются типами находящихся в них частиц, а переходы между состояниями имитируют ФХП. Моделирование проводится прямой имитацией случайных элементарных актов перестройки атомно-молекулярной структуры объекта с помощью генератора случайных чисел.
В качестве такого подхода к комплексному моделированию ФХП автором статьи разработан новый вариант метода вероятностного клеточного автомата (ВКА) [1–3]. В данном варианте метода моделируемый объект рассматривается на микроскопическом уровне. Атомно-молекулярной структуре объекта ставится в соответствие сетка ячеек ВКА, состояния которых определяются типами находящихся в них частиц, а переходы между состояниями имитируют ФХП. Моделирование проводится прямой имитацией случайных элементарных актов перестройки атомно-молекулярной структуры объекта с помощью генератора случайных чисел.
Согласно базовому принципу предложенного метода [1–3], микроструктуре моделируемой системы ставится в соответствие сетка ячеек ВКА, каждая из которых представляет собой вероятностный автомат. Типам частиц ставятся в соответствие состояния ячеек S, а случайным процессам перестройки – переходы J ячеек между состояниями (буквами с надстрочными знаками обозначены состояния ячеек) [2, 3]:
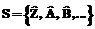 , (1)
, (1)
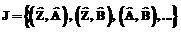 . (2)
. (2)
Случайные переходы на каждом шаге моделирования реализуются с вероятностями W, которые определяются на основании базовых физических принципов (например, молекулярно-кинетических, термоактивационных или квантово-механических):
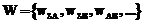 . (3)
. (3)
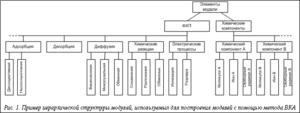
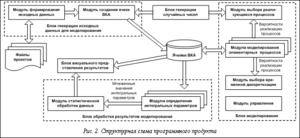 Отличительной особенностью предложенного метода ВКА является использование единой методологической позиции для моделирования широкого круга элементарных ФХП. Все процессы формально представляются в виде правил перестройки микроструктуры (например, при диффузии частица переходит из одной ячейки в соседнюю, при адсорбции пустая ячейка на межфазной поверхности заполняется частицей). Таким образом, в рамках разработанного метода элементарные ФХП и химические компоненты могут быть представлены в виде универсальной иерархической структуры модулей. Пример такой структуры показан на рисунке 1. Модули образуют две группы: ФХП и химические компоненты. Каждый модуль ФХП и компонента, в свою очередь, могут содержать различные варианты, связанные с состоянием частиц и механизмами ФХП. При необходимости разработчик может добавить в иерархию новые модули.
Отличительной особенностью предложенного метода ВКА является использование единой методологической позиции для моделирования широкого круга элементарных ФХП. Все процессы формально представляются в виде правил перестройки микроструктуры (например, при диффузии частица переходит из одной ячейки в соседнюю, при адсорбции пустая ячейка на межфазной поверхности заполняется частицей). Таким образом, в рамках разработанного метода элементарные ФХП и химические компоненты могут быть представлены в виде универсальной иерархической структуры модулей. Пример такой структуры показан на рисунке 1. Модули образуют две группы: ФХП и химические компоненты. Каждый модуль ФХП и компонента, в свою очередь, могут содержать различные варианты, связанные с состоянием частиц и механизмами ФХП. При необходимости разработчик может добавить в иерархию новые модули.
С формальной точки зрения постановка задачи моделирования в данном случае связана со следующими основными моментами.
1. Имеется физико-химическая система, представляющая собой распределение частиц (атомов или молекул) по рассматриваемому объему.
2. Разработчик модели выбирает модули, которые будут учитываться при моделировании физико-химической системы, а также интегральные параметры, на основании которых он будет принимать решение о структуре модели.
3. Проводится прямое имитационное моделирование ФХП в рассматриваемой системе, на основании которого определяются значения необходимых интегральных параметров системы.
 4. По значению полученных параметров разработчик модели принимает решение о необходимости учета в модели тех или иных модулей.
4. По значению полученных параметров разработчик модели принимает решение о необходимости учета в модели тех или иных модулей.
В рамках такого подхода разработчик модели может достаточно быстро формировать различные варианты ее структуры и проверять гипотезы о влиянии тех или иных компонентов и ФХП на интегральные показатели рассматриваемой системы.
Для практической реализации указанного подхода разработан специализированный программный продукт, структура которого представлена на рисунке 2. С помощью блока генерации исходных данных пользователь может выбрать химические компоненты и элементарные процессы, участвующие в моделировании, задать термодинамические условия в системе, а также сформировать модель атомно-молекулярной структуры объекта в начальный момент времени. Блок моделирования с помощью выбранных модулей непосредственно проводит имитацию ФХП в исследуемом объекте.
Непосредственными результатами моделирования являются распределения частиц системы по ячейкам ВКА. Для обеспечения возможности их использования служит блок обработки результатов моделирования. В нем на основании полученных атомно-молекулярных структур определяются значения интегральных параметров системы, удобных для дальнейшего использования (например, химический состав, масса, концентрация компонентов и т.д.).
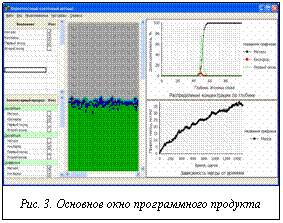
 На рисунке 3 представлено основное окно разработанного программного продукта при моделировании процессов газовой коррозии металлов. Пользователь может выбирать модули химических компонентов и процессов, задействованных в модели (таблицы в левой части окна), и настраивать их параметры. В центральной части окна пользователь наблюдает изменения, происходящие в атомно-молекулярной структуре системы с течением времени (на рисунке просматривается рост слоя оксида, образующегося на поверхности металла). Одновременно с этим разработчик модели видит необходимые ему значения интегральных параметров системы, полученные в ходе обработки состояний ячеек ВКА (в данном случае пользователь отслеживает распределение химического состава по глубине материала и изменение массы коррозирующего образца).
На рисунке 3 представлено основное окно разработанного программного продукта при моделировании процессов газовой коррозии металлов. Пользователь может выбирать модули химических компонентов и процессов, задействованных в модели (таблицы в левой части окна), и настраивать их параметры. В центральной части окна пользователь наблюдает изменения, происходящие в атомно-молекулярной структуре системы с течением времени (на рисунке просматривается рост слоя оксида, образующегося на поверхности металла). Одновременно с этим разработчик модели видит необходимые ему значения интегральных параметров системы, полученные в ходе обработки состояний ячеек ВКА (в данном случае пользователь отслеживает распределение химического состава по глубине материала и изменение массы коррозирующего образца).
Рассмотрим, например, использование разработанного программного продукта при принятии решений о структуре модели процессов, протекающих на границе металла с кислородом [1]. В качестве критерия, определяющего необходимость включения модуля, будем рассматривать изменение массы образца во времени Dm, обусловленное образованием оксида металла.
Выдвинем гипотезу № 1 о том, что в системе возможно протекание двух простейших процессов: адсорбции из газовой фазы на поверхности металла и десорбции с поверхности в газ. При этом система содержит два химических компонента: металл и кислород. Структура данной модели представлена на рисунке 4 в виде модулей, обозначенных сплошными линиями. Формализовав с помощью разработанного программного продукта указанную систему и проведя моделирование, получаем зависимость прироста массы от времени (рис. 5, график 1).
На следующем этапе оценим влияние химических процессов на параметры системы. Для этого примем гипотезу № 2 о том, что кислород может диффундировать в твердом теле и окислять атомы металла. В данном случае в структуру добавляются модули, обозначенные на рисунке 4 пунктирной линией. В результате моделирования такой системы с помощью разработанного программного продукта получаем определенную зависимость (рис. 5, график 2). Из результатов моделирования видно, что в данных конкретных условиях процессы окисления рассматриваемого металла играют существенную роль.
 Для проверки гипотезы № 3 о влиянии процессов вторичного окисления металла с образованием второго оксида в структурную модель системы включим процесс вторичного окисления и второй оксид (затонированные блоки на рис. 4). Проведя моделирование указанной системы, получаем результат, приведенный на рисунке 5 (график 3). Он в среднем аналогичен предыдущему варианту (различия обусловлены флуктуационным характером результатов моделирования). Из этого можно сделать вывод о том, что для данного случая процессы вторичного окисления не играют существенной роли.
Для проверки гипотезы № 3 о влиянии процессов вторичного окисления металла с образованием второго оксида в структурную модель системы включим процесс вторичного окисления и второй оксид (затонированные блоки на рис. 4). Проведя моделирование указанной системы, получаем результат, приведенный на рисунке 5 (график 3). Он в среднем аналогичен предыдущему варианту (различия обусловлены флуктуационным характером результатов моделирования). Из этого можно сделать вывод о том, что для данного случая процессы вторичного окисления не играют существенной роли.
Таким образом, в результате проведенного анализа разработчик может остановиться на структуре модели, предложенной в гипотезе № 2.
Основным ограничением данного програм- много продукта является то, что он пригоден для моделирования только тех ФХП, которые могут быть сведены к перестройке атомно-молекулярной структуры вещества. Его нельзя использовать для анализа молекулярно-кинетических явлений, тепловых процессов, конвекции, деформации и движения системы как единого целого.
В заключение можно сделать вывод о том, что описанный программный продукт представляет ценность для разработчиков математических моделей как на этапе предварительной проработки, так и в процессе их уточнения. Это особенно важно для моделей систем, в которых возможно возникновение эффектов, основанных на взаимовлиянии ФХП различной природы.
Литература
1. Агафонов А.Н. [и др.]. Разработка физических принципов и алгоритмов компьютерного моделирования базовых процессов формирования микроструктур методами вероятностного клеточного автомата // Вестн. СамГТУ. Сер.: Физ.-мат. науки, 2007. № 1. С. 99–107.
2. Коныгин С.Б., Лесухин С.П. Стохастическая модель окисления металлов в газовой среде // Изв. Самарского науч. центра РАН. 2010. Т. 12. № 1 (2). С. 377–380.
3. Коныгин С.Б. Применение метода вероятностного клеточного автомата к моделированию гетерогенных систем // Строительство нефтяных и газовых скважин на суше и на море. 2011. № 4. С. 30–31.




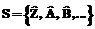 , (1)
, (1)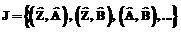 . (2)
. (2)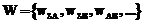 . (3)
. (3)
 4. По значению полученных параметров разработчик модели принимает решение о необходимости учета в модели тех или иных модулей.
4. По значению полученных параметров разработчик модели принимает решение о необходимости учета в модели тех или иных модулей.

