Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Моделирование оптимальных условий биосинтеза
Аннотация:Рассмотрены условия, обеспечивающие максимальное значение продуктивности целевого продукта в ферментёре с перемешиванием, в котором протекает процесс микробиологического синтеза с нелинейной кинетикой роста микроорганизмов. Получены расчетные соотношения для оптимальных условий и возможности оценки неединственности стационарных режимов. Приведены численные результаты, подтверждающие теоретические выводы.
Abstract:The conditions providing the maximum productivity value of a target product in stirred fermenter in which process of microbiological synthesis with nonlinear кинетикой growth of microorganisms proceeds are considered. Equations for optimal conditions calculation and estimations of possibility non-uniqueness stationary modes are received. The numerical results confirming theoretical conclusions are presented.
| Авторы: Гордеева Ю.Л. (l.s.gordeev@yandex.ru) - Московская государственная академия ветеринарной медицины и биотехнологии им. К.И. Скрябина, Москва, Россия, кандидат технических наук | |
| Ключевые слова: информационные технологии, максимальная продуктивность, нелинейная кинетика, моделирование |
|
| Keywords: information technologies, maximum productivity, nonlinear kinetics, modeling |
|
| Количество просмотров: 12793 |
Версия для печати Выпуск в формате PDF (5.05Мб) Скачать обложку в формате PDF (1.39Мб) |
Информационные технологии биотехнологических процессов базируются на использовании математических моделей для описания микробиологического синтеза. Моделирование обусловлено необходимостью выбора адекватного описания кинетики процесса, которое должно учитывать одновременно протекающие процессы на микроуровне (в клетках), в микробных популяциях, на макроуровне (массо- и теплообмен в системе, гидродинамическая обстановка и т.п.). Адекватное описание кинетики можно получить в результате многочисленных экспериментальных исследований, что зачастую затруднительно в силу ряда объективных причин (техническая сложность постановки эксперимента, сложность или невозможность прямых измерений показателей процесса, часто наблюдаемая невоспроизводимость результатов из-за невозможности учета всей совокупности факторов и др.).
Для моделирования оптимальных условий биосинтеза рассмотрим процесс, математическая модель которого представлена системой уравнений [3]:
где D=Q/V, ч–1; V – объем реактора, л; Q – объемная скорость потока, л/ч; m – удельная скорость роста биомассы, ч–1; YX/S – стехиометрический коэффициент, г/г; X, S, P – концентрация биомассы, субстрата и продукта соответственно на выходе из реактора, г/л; Sf – концентрация субстрата в потоке, поступающем в реактор, г/л; a, b – константы. Удельная скорость роста записана в виде
где mm – максимальная удельная скорость рос- та, ч–1; Pm – константа насыщения продукта, г/л; Ki – константа ингибирования субстрата, г/л; Km – константа насыщения субстрата, г/л. Из первого уравнения системы (1) получаем D=m. (3) Данное соотношение означает, что величины D и m имеют взаимоограничение, то есть величина протока D должна соответствовать удельной скорости роста. Решение (1) относительно концентрации субстрата S на выходе из реактора имеет вид
где
Выбор знака (±) в выражении (4) определяется условием ограничения для S: 0£S£Sf. (8) Знак равенства в (8) относится к предельным случаям. Таким образом, для X и P имеем
P=X×(a+b/D). (10) Формула расчета продуктивности D×P (производительности по целевому компоненту P) имеет вид D×P=X×(a×D+b). (11) Анализ полученных соотношений показывает следующее. Если в процессе субстрат исчерпывается полностью, то есть S=0, удельная скорость роста m обращается в нуль и процесс ферментации не протекает. Если концентрация продукта достигает значения Pm (или близка к нему), удельная скорость роста также равна нулю. Это означает, что предельное максимальное значение P не может превышать Pm. Величина протока D, как отмечалось ранее, ограничена условием (3). Это свидетельствует о том, что максимальное значение D в процессе должно быть меньше величины, определяющей полное вымывание субстрата из аппарата. Очевидно, что тогда образование продукта не происходит. Математически это означает, что P=0, и тогда из (2) получаем максимальное значение D:
Таким образом, в соотношениях (4)–(11) 0 где maxD вычисляется по формуле (12) для любого значения Sf.
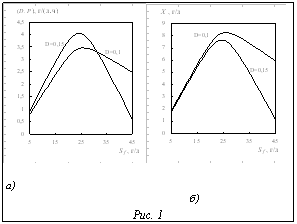
На рисунке 1а показана зависимость продуктивности D×P от концентрации субстрата в поступающем потоке Sf при различных величинах протока D, на рисунке 1б – зависимость концентрации биомассы X от Sf при различных D. Как и для первых двух зависимостей, экстремум по концентрации биомассы X достигается при таком же значении Sf, что и по P, и по D×P. Отсюда следует, что оптимальное значение Sf при заданном значении D доставляет максимум по P, D×P и X. Влияние скорости протока D на продуктивность D×P и концентрацию биомассы X показано на рисунке 2. Эти зависимости также носят экстремальный характер, при этом наиболее сильно экстремум проявляется при высоких значениях концентрации субстрата Sf. Представленные результаты получены для численных значений параметров [1–3], приведенных в таблице.
Необходимо отметить, что экстремальные характеристики отражают возможность существования неединственности стационарных состояний. Условие существования неединственности по Sf приведено в работе [3]. Для определения оптимальных условий (условий максимума D и D×P) воспользуемся соотношениями (2) и (3). Имеем
Необходимое условие существования экстремума P по S
Отсюда получаем Sopt=(Km×Ki)1/2. (16) Максимальная концентрация продукта будет следующей:
а максимальное значение продуктивности max(D×P)=
Для вычисления значений Sf и D, соответствующих максимальным значениям P и D×P, используем соотношение (4), где S=(Km×Ki)1/2, то есть
Используя (19), с целью определения
Расчет величины протока Dopt, обеспечивающей максимальное значение P и D×P для любого значения концентрации Sf в поступающем потоке, выполняется по соотношению
где
Знак корня в выражении (21) определяется условием неотрицательности Dopt и с учетом ограничения (12). На рисунке 3 приведены зависимости концентрации субстрата Sf и максимальной продуктивности D×P от скорости протока D при оптимальных условиях. Отметим следующее. Существование оптимальных условий в соответствии с соотношением (20) накладывает ограничение на величину протока D. По формуле (16) концентрация субстрата в поступающем потоке не может быть меньше (Km×Ki)1/2. Эта величина обеспечивается значением D в пределах
Ограничение (25) является ограничением для использования формулы (20). При этом верхнее ограничение для D определяется только значениями кинетических констант. В приведенных примерах (рис. 1, 2) для данных таблицы верхнее ограничение D=0,32718 ч–1. С другой стороны, использование формулы (21) для расчета Dopt при значении Sf тоже имеет ограничение, связанное с условием неотрицательности дискриминанта в (21), то есть
Последнее формирует условие максимального значения Sf, при котором имеется возможность оценить Dopt. Это значение рассчитывается по соотношению
где Таким образом, для приведенных численных значений кинетических констант максимальное значение Sf, для которого можно использовать формулу (21), будет равно Sf=25,8181 г/л (знак корня в выражении (27) определяется допустимым значением Sf). Если формулы для расчета оптимальных показателей использовать нельзя, продуктивность рассчитывается по формулам (4), (9)–(11). Разработка информационных технологий для биотехнологических процессов включает использование математических моделей, базирующихся на достоверных результатах экспериментальных исследований. Выполненный анализ оптимальных условий для микробиологического синтеза с нелинейной кинетикой роста микроорганизмов выявил возможность проведения процесса, обеспечивающего максимальную производительность по продукту с одновременным достижением максимальной концентрации по биомассе, позволил оценить ограничения и прогнозировать существование неединственности стационарных режимов по концентрации субстрата в поступающем потоке и по величине протока. В то же время информационные технологии предполагают создание библиотеки алгоритмов, обеспечивающих практическую реализацию результатов моделирования для конкретных постановок задачи. Литература 1. Agarwal P., Koshy G., Ramirez M. An algorithm for operating a fed-batch fermentor at optimum specific-growth // Biotechnol. Bioeng. 1989. № 33, pp. 115–125. 2. Henson M.A., Seborg D.E. Nonlinear control strategies for continuous fermenters // Chem. Eng. Sci. 1992. № 47, pp. 821–835. 3. Kumar G.P., Subrahmanya J.V.K., Chidambaram M. Periodic operation of a bioreactor with input multiplicities // Can. J. Chem. Eng. 1993. № 71, pp. 766–770. 4. McLain R.B. [et al.]. Habituating control for nonsquare nonlinear processes // Ind. Eng. Chem. Res. 1996. № 35, pp. 4067–4077. 5. Ruan L., Chen X.D. Comparison of several periodic operations of a continuous fermentation process // Biotechnol. Prog. 1996. № 12, pp. 286–288. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2840 |
Версия для печати Выпуск в формате PDF (5.05Мб) Скачать обложку в формате PDF (1.39Мб) |
| Статья опубликована в выпуске журнала № 3 за 2011 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Программная система исследований динамики технологических процессов формования химических волокон
- Программа идентификации условий теплообмена для изделий плоской формы
- Программный комплекс планирования производства на малом предприятии
- Алгоритм и программа расчета напряженно-деформированного состояния песчаных грунтов при циклическом нагружении
- Моделирование систем массового обслуживания с абсолютным приоритетом
Назад, к списку статей



 Таким образом, формирование информационной технологии для биотехнологических процессов прежде всего должно базироваться на использовании кинетических соотношений, получивших достаточное обоснование в экспериментальных исследованиях. Совершенствование техники эксперимента приводит к постепенному переходу от наиболее простых кинетических моделей к более усложненным соотношениям, которые отражают нелинейные взаимодействия в процессах синтеза. Последнее часто дает возможность прогнозировать оптимальные условия синтеза, существование множественности режимов синтеза и условий устойчивого функционирования. В данной работе рассматривается процесс микробиологического синтеза в аппарате непрерывного действия (его кинетическая модель обоснована в публикациях [1–5]).
Таким образом, формирование информационной технологии для биотехнологических процессов прежде всего должно базироваться на использовании кинетических соотношений, получивших достаточное обоснование в экспериментальных исследованиях. Совершенствование техники эксперимента приводит к постепенному переходу от наиболее простых кинетических моделей к более усложненным соотношениям, которые отражают нелинейные взаимодействия в процессах синтеза. Последнее часто дает возможность прогнозировать оптимальные условия синтеза, существование множественности режимов синтеза и условий устойчивого функционирования. В данной работе рассматривается процесс микробиологического синтеза в аппарате непрерывного действия (его кинетическая модель обоснована в публикациях [1–5]).
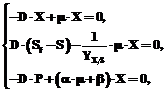 (1)
(1) , (2)
, (2)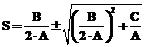 , (4)
, (4)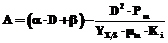 ; (5)
; (5) ; (6)
; (6)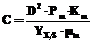 . (7)
. (7)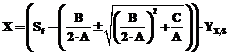 , (9)
, (9)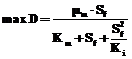 . (12)
. (12)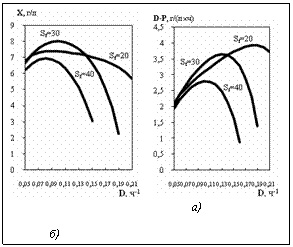 Целью дальнейшего анализа является определение условий, при которых обеспечивается максимальная концентрация целевого продукта P на выходе из ферментёра, условий получения максимальной продуктивности по целевому продукту P – D×P, максимальной концентрации биомассы X. Входными переменными являются концентрация субстрата в поступающем потоке Sf и величина протока D (соответствует объемной скорости поступающего потока Q при постоянном объеме заполнения V).
Целью дальнейшего анализа является определение условий, при которых обеспечивается максимальная концентрация целевого продукта P на выходе из ферментёра, условий получения максимальной продуктивности по целевому продукту P – D×P, максимальной концентрации биомассы X. Входными переменными являются концентрация субстрата в поступающем потоке Sf и величина протока D (соответствует объемной скорости поступающего потока Q при постоянном объеме заполнения V).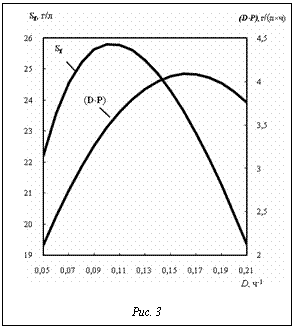
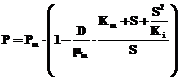 . (14)
. (14)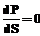 . (15)
. (15)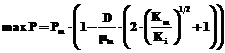 , (17)
, (17)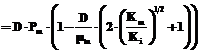 . (18)
. (18)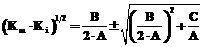 . (19)
. (19)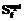 для любого значения величины протока D получим соотношение:
для любого значения величины протока D получим соотношение: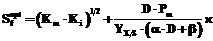
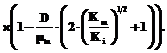 (20)
(20)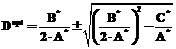 , (21)
, (21)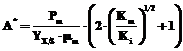 ; (22)
; (22)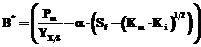 ; (23)
; (23)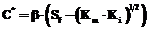 . (24)
. (24) . (25)
. (25)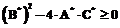 . (26)
. (26)
 (27)
(27)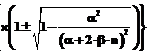 ,
, .
.