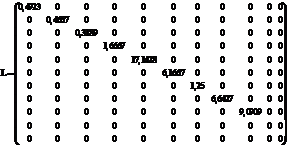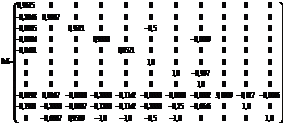Для достижения определенных целей в работе любой экономической системы необходимо управление, поэтому задачи оптимального управления в балансовых динамических моделях более адекватны для решения реальных экономических задач. В зависимости от характера и цели управления могут быть поставлены различные типы задач оптимального управления. Так, для невы- рожденных балансовых моделей А.Г. Гранберг, В.Ф. Кротов, Б.А. Лагоша и др. в своих работах рассматривали решение задачи нахождения оптимального управления при максимизации функции потребления в качестве функционала качества. Такая постановка задачи более соответствовала плановой экономике, и при переходе к рынку исследования в этом направлении стали крайне редкими.
В данной статье представлен алгоритм программы для нахождения приближенного решения задач оптимального и жесткого управления для вырожденных балансовых динамических моделей. Причем экономический смысл используемого функционала качества позволяет решать управленческие задачи для динамической балансовой модели экономической системы в условиях рыночной экономики.
Пусть L и M – квадратные матрицы порядка n, причем detL=0. Матрица М называется (L, p)-регулярной, если существует число μÎС такое, что det(μL-M)-1≠0, и существует pÎ{0}ÈN такое, что при p=0 в точке ∞ L-резольвента (μL-M)-1 матрицы M имеет устранимую особую точку; а в противном случае p равно порядку полюса в точке ∞. (Здесь и далее терминологию, понятия и результаты см. в [1].)
Рассмотрим линейную неоднородную систему обыкновенных дифференциальных уравнений
L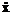 (t)=Mx(t)+f(t), (1)
(t)=Mx(t)+f(t), (1)
где fÎCp+1((0; t); Rn)ÇCp([0; t]; Rn).
В случае detL=0 в [2] предложено систему (1) называть системой леонтьевского типа, имея в виду ее прототип – динамическую балансовую модель В. Леонтьева с учетом запасов [3].
Вектор-функцию xÎC1([0; t]; Rn), обращающую (1) в тождество при некоторой вектор-функции f=f(t), назовем решением системы (1). Решение x=x(t) системы (1) будет решением задачи Шоуолтера–Сидорова, если при некоторых x0ÎRn справедливо
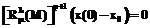 , (2)
, (2)
где 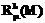 =(μL–M)-1L – правая L-резольвента М.
=(μL–M)-1L – правая L-резольвента М.
Заметим, если detL≠0, то задачи Шоуолтера–Сидорова и Коши
x(0)=x0 (3)
 эквивалентны; если detL=0, то из существования решения задачи (1), (2) следует существование решения (1), (3), обратное, вообще говоря, неверно.
эквивалентны; если detL=0, то из существования решения задачи (1), (2) следует существование решения (1), (3), обратное, вообще говоря, неверно.
В [2] предложен алгоритм численного решения задачи (1), (3). Одним из его этапов являетcя проверка принадлежности начальных условий фазовому пространству уравнения (1), она вызывает значительные трудности при численных расчетах и приводит к ограничению на размер матриц (n£5). Для преодоления этого ограничения в [4] вместо условия (3) используется условие (2) и предложен алгоритм численного решения (1), (2).
Для постановки задач оптимального и жесткого управления введем в рассмотрение пространства управления U:
U=Hp+1(Rn)={uÎL2((0, t), Rn):
u(p+1)ÎL2((0, t), Rn), pÎ{0}ÈN}
и состояния X:
X=H1(Rn)={xÎL2((0, t), Rn): 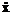 ÎL2((0, t), Rn)}.
ÎL2((0, t), Rn)}.
Пусть множество допустимых управлений U∂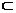 U является выпуклым и компактным.
U является выпуклым и компактным.
Задача оптимального управления заключается в нахождении среди множества допустимых пар u×x(u, f)ÎU∂×X почти всюду на (0, τ) пары, удовлетворяющей системе леонтьевского типа:
L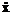 (t)=Mx(t)+f(t)+Bu(t) (4)
(t)=Mx(t)+f(t)+Bu(t) (4)
с начальным условием (2) такой v×x(v, f), что
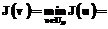
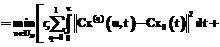 (5)
(5)
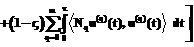 ,
,
где m может принимать значения от 0 до p+1, выбор значения связан со смыслом функционала в определенной прикладной задаче; Cx(u, t) и Cx0(t) – фактическая и планируемая функции наблюдаемой величины; zÎ(0, 1) – весовой коэффициент цели управления, заключающейся в достижении плановых показателей наблюдаемой величины; 1–z – весовой коэффициент цели управления, подразумевающей минимизацию расходуемых для этого ресурсов управления.
Задача жесткого управления состоит в нахождении среди множества допустимых пар u×x(u, f)ÎU∂×X почти всюду на (0, τ) пары, удовлетворяющей системе леонтьевского типа (4), с начальным условием (2) такой v×x(v, f), что
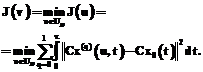 (6)
(6)
В [5] предложен метод численного решения задачи (2), (4), (5), в котором пространство управлений Hp+1(Rn) заменяется на конечномерное пространство 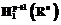 вектор-многочленов вида
вектор-многочленов вида
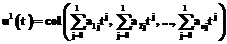 .
.
Пусть K=max{k1, k2}, 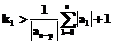 ,
, 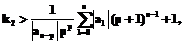 al – коэффициенты; n-p – степень многочлена det(μL-M). В качестве множества допустимых управлений будем рассматривать
al – коэффициенты; n-p – степень многочлена det(μL-M). В качестве множества допустимых управлений будем рассматривать 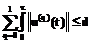 .
.
Справедливы следующие теоремы.
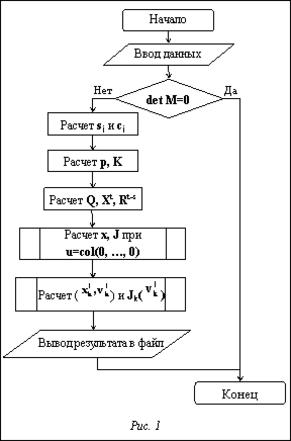
Теорема 1. Пусть матрица М – (L, p)-регулярна, pÎ{0}ÈN, кроме того, detM≠0 и множество допустимых управлений U∂ выпукло и компактно. Приближенное решение задачи (2), (4), (5) (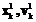 ) (
) (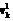 – точка минимума функционала) при k>K имеет вид
– точка минимума функционала) при k>K имеет вид
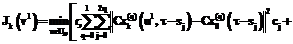
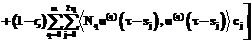 ; (7)
; (7)
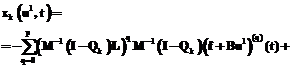
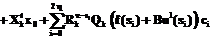 , (8)
, (8)
η, sj и сj – порядок, узлы и вес квадратурной формулы Гаусса соответственно,  ,
,
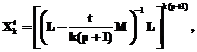
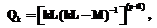
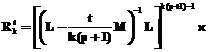
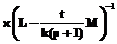 .
.
Теорема 2. В условиях теоремы 1 приближенное решение задачи (2), (4), (6) (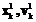 ) (
) (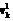 – точка минимума функционала) при k>K имеет вид
– точка минимума функционала) при k>K имеет вид
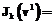
 (9)
(9)
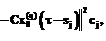
xk(ul, t) задается по формуле (8); 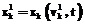 , причем η, sj и cj – соответственно порядок, узлы и вес квадратурной формулы Гаусса.
, причем η, sj и cj – соответственно порядок, узлы и вес квадратурной формулы Гаусса.
Алгоритм программы
Программа, реализующая алгоритм численного решения задач оптимального и жесткого управления для вырожденных линейных систем дифференциальных уравнений, написана на языке С++.
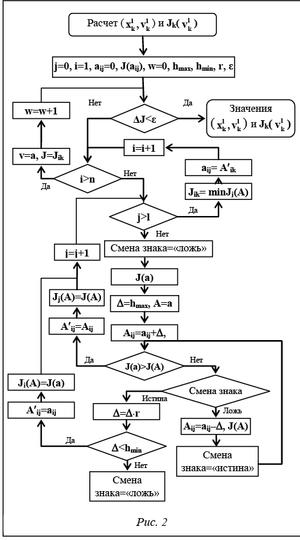 Программа построена как консольное приложение, ее вход представляет собой конфигурационный файл текстового формата. В нем указываются выбранная задача управления; имена файлов, в которых записаны массивы, входящие в состав системы и функционала качества; значения параметров расчета. Отметим, что f(t) и x0(t) задаются как массивы коэффициентов, число их строк равно числу компонент n, а число столбцов – l+1. Выходом программы является протокол расчета, массивы с итогом расчета дополнительно сохраняются в текстовый файл. На рисунке 1 представлена блок-схема программы. Условие detM≠0 не ограничивает общности рассуждений; проведя замену x=eλtz в уравнении (1), получим M'=M-λL, но detM'≠0.
Программа построена как консольное приложение, ее вход представляет собой конфигурационный файл текстового формата. В нем указываются выбранная задача управления; имена файлов, в которых записаны массивы, входящие в состав системы и функционала качества; значения параметров расчета. Отметим, что f(t) и x0(t) задаются как массивы коэффициентов, число их строк равно числу компонент n, а число столбцов – l+1. Выходом программы является протокол расчета, массивы с итогом расчета дополнительно сохраняются в текстовый файл. На рисунке 1 представлена блок-схема программы. Условие detM≠0 не ограничивает общности рассуждений; проведя замену x=eλtz в уравнении (1), получим M'=M-λL, но detM'≠0.
Процедуру расчета x и функционала качества J при u=col(0, …, 0) в виде блок-схемы приводить нецелесообразно, так как расчеты сводятся к использованию (8) для каждой компоненты.
Основная процедура поиска решения задачи оптимального или жесткого управления сводится к поиску массива коэффициентов вектор-многочленов ul, обозначаемого в блок-схеме (рис. 2) как матрица А. При поиске коэффициентов, при которых достигается минимум функционала, используются идеи покоординатного многошагового спуска и методов аппроксимации функции полиномом. В результате получаем многошаговый итеративный метод с использованием обновлений при подборе шага, с вычислением только аппроксимирующей функции и выполнением проверки условий ограничений на принадлежность множеству допустимых управлений и (в случае экономических приложений) неотрицательности значениий x или иных дополнительных ограничений. Градиент в данном подходе не используется из-за сложности функционала качества и больших погрешностей при численном дифференцировании. Процедура достаточно проста, поэтому скорость вычислений невелика, но алгоритм позволяет в дальнейшем распараллеливать процессы и купировать этот недостаток.
Завершение процедуры нахождения минимума функционала качества происходит по достижении абсолютной величины разности значений функционала последней и предпоследней итераций цикла меньшего значения, чем заданное ε.
Для исследования эффективности алгоритма в ходе вычислительных экспериментов применялись различные параметры шага (варьировалась величина его изменения r), порядок прохождения цикла по i (от 1 до n, от n до 1). Во всех случаях были получены результаты, различие между которыми менее 0,01 %.
Вычислительный эксперимент
Приведем результаты вычислительного эксперимента для вырожденной динамической балансовой модели небольшого предприятия. При составлении такой модели используется метод с учетом экспорта-импорта в денежной форме. Так, матрица L представляет удельные капитальные затраты, матрица M – разность единичной матрицы и матрицы удельных прямых затрат. В матрице L производительными являются все девять видов деятельности предприятия, а две последние нулевые строки отражают отсутствие капитальных вложений для двух групп внешних покупателей продукции предприятия – домашние хозяйства и организации. Вместе с тем наличие таких внешних структурных элементов в балансовой модели является обязательным для обеспечения условия замкнутости системы.
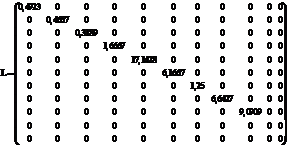
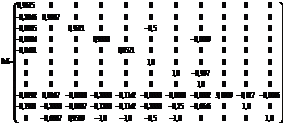
В качестве x(t) выступает вектор-функция выпуска продукции в денежных единицах. Плановые значения x0(t) и выпуск конечного продукта f(t) примем постоянными: x0(t)=f(t)=col(52, 600, 313,5, 90, 87,5, 300, 1200, 300,9, 110, 880, 2167,5).
Начальными параметрами расчета были приняты: степень полиномов компонент вектор-функции управления равна 7; максимальный и минимальные шаги составили соответственно 100 и 0,000001; изменение шага r=0,5; точность расчета значения функционала качества ε=0,1. При расчете используется тип переменных double, то есть с плавающей запятой и 11 значащими цифрами после нее. В качестве ограничения на множество допустимых управлений принимается d=10000. Значения объема выпускаемой продукции должны быть неотрицательными, а значения управления могут быть как отрицательными, так и положительными. Отрицательные значения управления некоторой компоненты, то есть вида деятельности предприятия, свидетельствуют о том, что этот вид деятельности приносит прибыль предприятию, а положительные – предприятие является дотационным. Весовой коэффициент был принят равным 0,5, то есть цели управления рассматриваются в равной степени значимыми.
В результате расчета получены значения p=2, K=657.
В качестве расчетного принимается временной промежуток 1 год, таким образом, τ=1. Рассчитываются значения x(t) помесячно. В результате получим следующее решение задачи оптимального управления:
u1(t)= –135,687+329,968t–170,74t2– –51,194t3+70,282t4+15,9302t5–1,0452t6–11,1995t7,
u2(t)= –156,579+271,71t–189,123t2– –55,786t3+87,0056t4+16,342t5–3,9215t6–11,695t7,
u3(t)=133,911+301,159t–274,853t2– –78,8574t3+135,0098t4+30,639t5–16,05225t6–14,312t7,
u4(t)= –1297,53+3489,55t–1437,11t2– –384,76t3+455,56t4+225,708t5–17,212t6–102,478t7,
u5(t)= –1904,59+3247,46t–1254,68t2– –363,77t3+454,34t4+149,66t5–9,033t6–84,29t7,
u6(t)= –370,422+10532,23t–4215,82t2– –134,52t3+172,607t4+51,147t5–20,385t6–20,202t7,
u7(t)=3738,525+10145,51t–4660,645t2– –133,667t3+177,185t4+52,978t5–2,899t6–31,982t7,
u8(t)=1168,896+31587,5t–590,625t2– –179,443t3+223,511t4+74,707t5–19,4702t6–32,745t7,
u9(t)= –252,441+484,619t–203,369t2– –7,5988t3+4,104t4+4,2419t5+0,122t6–1,591t7,
u10(t)=1308,105–2806,885t+632,934t2+ +13,854t3+5,6152t4+16,998t5–0,7171t6+4,226t7,
u11(t)=3293,945–3523,682t+708,984t2+ +19,409t3–13,885t4+13,733t5–1,342t6–4,318t7.
Так, первый вид деятельности в начале планируемого периода является доходным для предприятия – значение управления отрицательно и составляет –135,687 усл. ден. ед., а в конце периода (при t=1) требует дотационных средств в размере 46,3143 усл. ден. ед. Одиннадцатый вид деятельности на протяжении всего планируемого периода является дотационным, а девятый – доходным, за счет него могут финансироваться другие виды деятельности. Такого рода анализ может проводиться для всех видов деятельности в выбранный момент времени (из планируемого периода) для предприятия. Значение функционала качества составит 8,245486×1010. Ряд значений x=x(t) приведен в таблице.
Вычислительный эксперимент показал, что при планировании постоянного выпуска продукции предприятия на основе решения задачи оптимального управления такие значения переменных могут считаться неэффективным решением. Для преодоления этого необходимо уточнение модели и наложение более строгих ограничений, чем неотрицательность, на значения каждой компонен- ты x(t). Кроме того, одной из рекомендаций может являться пересмотр весовых коэффициентов целей управления: так, для данного предприятия – с такой структурой затрат и капитальных вложений – цель управления минимизации управляющих воздействий должна рассматриваться с меньшим весовым коэффициентом, чем цель достижения плановых показателей. (Безусловно, с учетом ошибок, связанных с недостатками финансового учета на предприятии, так как балансовая модель строится на основе данных предприятия о структуре себестоимости и учета основных средств.)
Результаты значений x=x(t) как решений задачи оптимального управления
|
xj(t)
|
t=0
|
t=1/12
|
t=1/2
|
t=1
|
|
x1(t)
|
52
|
2,521
|
32,973
|
158,683
|
|
x2(t)
|
600
|
89,238
|
427,242
|
982,684
|
|
x3(t)
|
313,5
|
383,397
|
637,98
|
854,628
|
|
x4(t)
|
90
|
8,352
|
15,934
|
36,874
|
|
x5(t)
|
87,5
|
5,251
|
10,642
|
23,572
|
|
x6(t)
|
300
|
224,392
|
229,929
|
428,979
|
|
x7(t)
|
1200
|
2449,322
|
3132,282
|
4225,199
|
|
x8(t)
|
300,9
|
269,243
|
241,727
|
227,156
|
|
x9(t)
|
110
|
112,788
|
131,638
|
138,5201
|
|
x10(t)
|
88
|
23,54
|
11,432
|
353,164
|
|
x11(t)
|
2167,5
|
605,36
|
1383,061
|
5281,761
|
Таким образом, использование решения задач оптимального управления для вырожденных балансовых моделей предприятия в планировании и анализе его деятельности имеет практическое значение, подтверждаемое специалистами предприятия, на базе которого была построена модель и проведены вычислительные эксперименты.
Литература
1. Sviridyuk G.A., Fedorov V.E. Linear Sobolev Type Equations and Degenerate Semi-groups of Operators.-Utrecht-Boston-Köln-Tokyo: VSP, 2003.
2. Свиридюк Г.А., Брычев С.В. Численное решение систем уравнений леонтьевского типа // Изв. вузов: сер. Математика. 2003. № 8. С. 46–52.
3. Леонтьев В.В. Межотраслевая экономика. М.: Экономика, 1997. 487 c.
4. Келлер А.В. Алгоритм решения задачи Шоуолтера–Сидорова для моделей леонтьевского типа // Вестн. ЮУрГУ: сер. Математическое моделирование и программирование. Челябинск, 2011. № 4. Вып. 7. С. 40–46.
5. Келлер А.В. Системы леонтьевского типа: классы задач с начальным условием Шоуолтера–Сидорова и численные решения // Изв. ИГУ: сер. Математика. Иркутск. 2010. № 2. С. 30–43.



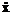 (t)=Mx(t)+f(t), (1)
(t)=Mx(t)+f(t), (1)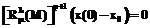 , (2)
, (2)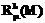 =(μL–M)-1L – правая L-резольвента М.
=(μL–M)-1L – правая L-резольвента М.
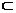 U является выпуклым и компактным.
U является выпуклым и компактным.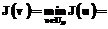
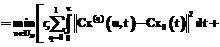 (5)
(5)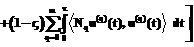 ,
,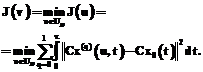 (6)
(6)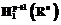 вектор-многочленов вида
вектор-многочленов вида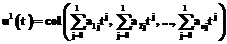 .
.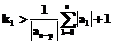 ,
, 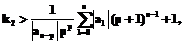 al – коэффициенты; n-p – степень многочлена det(μL-M). В качестве множества допустимых управлений будем рассматривать
al – коэффициенты; n-p – степень многочлена det(μL-M). В качестве множества допустимых управлений будем рассматривать 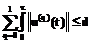 .
.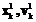 ) (
) (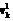 – точка минимума функционала) при k>K имеет вид
– точка минимума функционала) при k>K имеет вид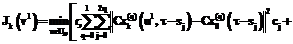
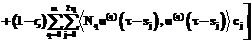 ; (7)
; (7)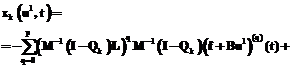
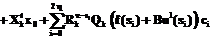 , (8)
, (8) ,
,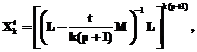
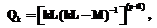
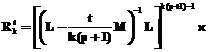
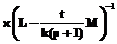 .
.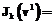
 (9)
(9)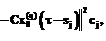
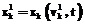 , причем η, sj и cj – соответственно порядок, узлы и вес квадратурной формулы Гаусса.
, причем η, sj и cj – соответственно порядок, узлы и вес квадратурной формулы Гаусса.