Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Тестирование программ с использованием генетических алгоритмов
Аннотация:В статье рассматриваются проблемы проведения сертификационного тестирования постоянно обновляющихся программных средств. Предложен подход к построению тестовой базы с использованием генетических алгоритмов.
Abstract:The problems of carrying out of certification test frequently updated software tools are considered in the article. The main idea of the article is the construction of test base with a genetic algorithm.
| Авторы: Мельникова В.В. (viklipse@mail.ru) - Тверской государственный технический университет, Тверь, Россия, Аспирант , Котов С.Л. (info@gicpsvt.ru) - Главный испытательный сертификационный центр безопасности программных средств и вычислительной техники (доцент, директор), Тверь, Россия, кандидат экономических наук, Палюх Б.В. (pboris@tstu.tver.ru) - Тверской государственный технический университет (профессор), г. Тверь, Россия, доктор технических наук, Проскуряков М.А. (gic@tvcom.ru) - Главный испытательный сертификационный центр программных средств вычислительной техники | |
| Ключевые слова: метрики тестового покрытия, генетические алгоритмы, автоматизированная тестовая база, сертификационное тестирование |
|
| Keywords: metrics of test covering, genetic algorithm, automated test base, certification test |
|
| Количество просмотров: 13386 |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
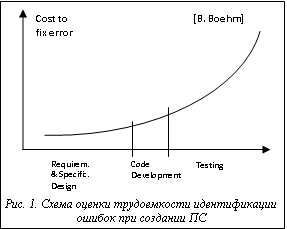
При разработке программных средств (ПС), к качеству которых предъявляются повышенные требования, перед вводом системы в эксплуатацию со стороны уполномоченного органа (обычно государственного) требуется подтверждение соответствия ее эксплуатационных характеристик заданным критериям. Такое соответствие определяется в ходе сертификации ПС, направленной на получение сертификата соответствия либо сертификата качества. Зачастую ПС разрабатываются в сжатые сроки и при ограниченных бюджетах. Затем они постоянно дорабатываются с целью исправления выявленных ошибок или отслеживания изменений предметной области применения ПС (например, при изменении законодательства). В результате ПС становятся версионными, причем обновления могут происходить довольно часто. Каждая новая версия требует повторной сертификации [1]. В связи с тем, что средства защиты информации (СЗИ), операционные системы, некоторые прикладные программы нередко жизненно важны для многих организаций, остро встает проблема быстрого прохождения сертификации очередной версии таких ПС. Наличие сертификата необходимого образца является гарантией соответствия ПС определенным стандартам, что позволяет использовать его в оговоренных условиях эксплуатации. Для современного противостояния киберпреступности в индустрии разработки СЗИ особую важность приобретает временной фактор. Длительное проведение сертификации ПС СЗИ снижает уровень защищенности пользователей. При этом обновления ПС могут происходить быстрее сертификации его очередной версии. Кроме того, затраты на сертификацию и последующий инспекционный контроль за стабильностью характеристик сертифицированного, но постоянно обновляющегося ПС, обеспечивающих (определяющих) выполнение этих требований, могут свести на нет все преимущества от его использования. Главной составляющей процедуры проведения сертификационных испытаний и одним из наиболее устоявшихся способов обеспечения качества разработки ПО представляется тестирование. Оно входит в набор эффективных средств современной системы обеспечения качества программного продукта. Тестирование позволяет достаточно полно оценить трудоемкость ПС. Широко известна оценка распределения трудоемкости между фазами создания программного продукта: 40 %–20 %–40 % (рис. 1), из чего следует, что наибольший эффект в снижении трудоемкости может быть получен прежде всего на фазах тестирования (Testing) и проектирования (Design) [2].
Предложенная в [3] методика проведения сертификационных испытаний основывается главным образом на создании и использовании автоматизированной тестовой базы, предполагающей создание тестов на основе анализа функциональных требований. Общая схема создания тестовой базы представлена на рисунке 2. Функциональные требования должны ранжироваться в зависимости от их сложности и важности. Для их проверки необходимы две категории тестов: тесты по спецификациям и тесты для ситуаций, не отраженных в требованиях. Целью тестов первой группы является демонстрация способности ПС давать отклик на допустимые исходные данные и условия в соответствии с требованиями. Цель тестов второй группы – демонстрация способности ПС адекватно реагировать на недопустимые входные данные и условия, иными словами, предотвращение отказа ПС. Далее отранжированные функциональные требования формализуются и записываются в виде спецификаций. На этапе разработки тестов важно сформулировать требования к качеству тестирования, а именно: какой уровень тестового покрытия (например, количество тестов) будет считаться достаточным для прекращения тестирования. Существуют различные подходы к решению задачи автоматической генерации тестов. В данной статье предлагается применение для этого генетических алгоритмов. Известно, что генетические алгоритмы – это метод решения задач оптимизации с использованием идей, почерпнутых из эволюционной биологии: наследование признаков, мутация, естественный отбор и кроссовер [4]. Определяется множество кандидатов, которые представляются в виде списков, деревьев или иных структур данных, и среди них ищется решение задачи [5]. Предлагаемый подход использования генетических алгоритмов заключается в поиске с его помощью тестовых значений и генерации кода тестов. Основная сложность состоит в выборе функции приспособленности для особей популяции. Задача поиска значений для создания теста сводится таким образом к оптимизационной задаче при помощи подбора соответствующей функции приспособленности.
Общая схема генетического алгоритма выглядит следующим образом. 1. Создать начальный набор кандидатов. 2. Оценить качество каждого кандидата в текущем наборе. 3. Выбрать пары наиболее качественных кандидатов для воспроизводства. 4. Применить оператор кроссовера. 5. Применить оператор мутации. 6. Если не выполнено условие останова, перейти к шагу 2. Начальный набор кандидатов, как правило, формируется случайным образом. На множестве кандидатов определяется оценочная функция, задающая качество кандидата, то есть насколько он близок к верному решению. При выборе кандидатов для воспроизводства больше шансов имеют более качественные из них. По двум выбранным кандидатам предыдущего поколения оператор кроссовера строит кандидата следующего поколения. Оператор мутации вносит малые случайные изменения из них. Алгоритм завершается, когда выполняется условие останова. Часто используются следующие условия останова: достигается заданное количество поколений, найдено верное решение, за заданное количество итераций максимальное качество кандидатов в популяции не улучшилось. Кроме того, возможны их различные комбинации. Для тестирования ПО требуется создать репрезентативный набор тестов, то есть набор, охватывающий все возможные сценарии работы системы. Для оценки репрезентативности тестовых наборов используются различные критерии полноты тестового покрытия. Пусть P – множество программных систем; T – множество тестов; Σ – множество тестовых наборов, то есть множество всех конечных подмножеств множества T. Тогда задача генерации тестов может быть сформулирована следующим образом: для заданной тестируемой системы S Многие критерии полноты тестового покрытия, имеющие практическое применение, строятся по следующей схеме: для тестируемой системы S критерий F определяет множество элементов тестового покрытия
Наиболее часто встречаются следующие критерии полноты тестового покрытия: - каждый оператор в исходном коде выполняется хотя бы один раз; - каждая ветвь графа потока управления выполняется хотя бы один раз; - каждый путь графа потока управления исполнением выполняется хотя бы один раз; - каждое логическое выражение хотя бы один раз вычисляется со значением «истина» и хотя бы один раз со значением «ложь»; - тестовый набор убивает всех мутантов в заданном наборе. Со многими критериями полноты тестового покрытия можно связать соответствующую метрику тестового покрытия, то есть функцию вида M:P´S®R. Значение этой функции M(S, s) имеет смысл числовой оценки того, насколько хорошо тестовый набор s покрывает тестируемую систему S. Сам критерий при этом можно записать в виде M(S, s)³aS, где aS – минимальное пороговое значение метрики M для тестируемой системы S. В частности, для критерия полноты тестового покрытия F, представимого в виде (1), можно ввести следующую метрику:
Сам критерий при этом примет вид
В случаях, когда не удается построить тестовый набор, удовлетворяющий такому критерию полноты тестового покрытия, можно использовать ослабленный критерий:
Параметр lÎ(0,1] указывает, какая доля элементов тестового покрытия должна быть покрыта тестовым набором. Наиболее часто упоминаемыми метриками тестового покрытия являются количество покрытых (выполненных хотя бы один раз) операторов в исходном коде, ветвей графа потока управления, путей графа потока управления, а также количество распознанных мутантов (версий тестируемой системы с искусственно привнесенными ошибками). Все эти метрики можно представить в виде (2). Рассмотрим простейший генетический алгоритм для задачи генерации: для заданной тестовой системы S и заданного элемента тестового покрытия q построить тест tÎT, удовлетворяющий условию f(q, t)=·. Для построения генетического алгоритма решения этой задачи необходимо определить множество кандидатов, структуру их представления, оценочную функцию, оператор кроссовера, оператор мутации, условие останова. В качестве множества кандидатов возьмем множество тестов T, критерием полноты тестового покрытия определим критерий покрытия путей потока управления. Тестовый набор удовлетворяет критерию покрытия путей потока управления, если его выполнение хотя бы один раз проходит по каждому возможному пути в графе потока управления, ведущему от точки входа до точки завершения работы. Каждый путь представляет собой последовательность переходов R=t1, t2, …, tn, где ti имеет вид Пусть есть два пути Обозначим через length(R) длину пути R, а через common(R¢, R²) максимальный размер общего упорядоченного подмножества путей R¢ и R². Определим оценочную функцию для критерия покрытия путей потока управления следующим образом: –mR(t)=length(R)+length(path(t))–2×common(R, path(t)). Здесь path(t) – путь, по которому приходит управление при выполнении теста t. Значение в правой части равно количеству переходов в путях R и path(t), не входящих в максимальное общее упорядоченное подмножество этих путей. Оно равно 0 тогда и только тогда, когда пути R и path(t) совпадают. Применение генетических алгоритмов для генерации тестов предъявляет дополнительные требования к используемым критериям полноты тестового покрытия. Это вызвано тем, что критерий полноты используется не только для оценки качества сгенерированных тестов, но и непосредственно в процессе генерации для оценки близости полученных тестов к нужным результатам. Таким образом, необходимо иметь оценочную функцию, позволяющую измерить эту близость, определить, насколько перспективными являются уже построенные тесты с точки зрения их использования в качестве основы для построения новых тестов. Для критериев, связанных с покрытием тех или иных путей в коде программы, удается построить достаточно удобные оценочные функции, основанные на количестве непокрытых дуг в пути, который нужно покрыть. Для оценки достаточности и полноты сформированных тестов можно воспользоваться мутационным критерием проверки: в программу P вносят мутации (то есть искусственно создают программы-мутанты P1, P2); затем программа P и ее мутанты тестируются на одном и том же наборе тестов (X, Y). Если на наборе (X, Y) подтверждается правильность программы P и, кроме того, выявляются все внесенные в программы-мутанты ошибки, то набор тестов (X, Y) соответствует мутационному критерию, а тестируемая программа объявляется правильной. Если некоторые мутанты не выявили всех мутаций, надо расширять набор тестов (X, Y) с использованием генетических алгоритмов и продолжать тестирование. После оценки и апробации сформированных с помощью генетического алгоритма тестов формируется тестовая база, которая впоследствии используется для проведения регрессионного тестирования. Таким образом, созданная с использованием генетических алгоритмов база тестов позволит значительно сократить время на проведение сертификационных испытаний и их трудоемкость. Экономический эффект достигается за счет экономии ресурсов, затраченных на повторное проведение сертификационных испытаний в целом, и составляет при цикле жизни приложения около трех лет от 20 до 45 %. Литература 1.Полежаев В.А., Семенов М.Н., Мельникова В.В. Автоматизированная система оценки уровня налоговых рисков // Программные продукты и системы. 2008. № 4 (84). 2.Котляров В.П., Коликова Т.В. Основы современного тестирования программного обеспечения, разработанного на с#: учеб. пособие; [под ред. В.П. Котлярова]. СПб, 2004. С. 55–57. 3.Котов С.Л., Демирский А.А., Мещерякова В.В. Проведение сертификационных испытаний часто обновляющихся ПС с использованием автоматизированной тестовой базы // Вестн. ВНИИМАШ, 2010. 4.Семенов Н.А. Интеллектуальные информационные системы: учеб. пособие. Тверь: Изд-во ТГТУ, 2004. 1-е изд. С. 87–89. 5.Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с польск. И.Д. Рудинского]. М.: Горячая линия – Телеком, 2006. С. 261–264. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=2926 |
Версия для печати Выпуск в формате PDF (5.83Мб) Скачать обложку в формате PDF (1.28Мб) |
| Статья опубликована в выпуске журнала № 4 за 2011 год. [ на стр. 107 – 110 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Метод автоматизации проектирования распределенной реляционной базы данных
- Верификация мультиагентных систем с помощью цепей маркова: оценка вероятности нахождения агентами оптимального решения
- Решение задачи структурного построения программного обеспечения интеллектуального датчика влажности
- Эволюционный алгоритм построения дерева решений
- Решение эталонной транспортной задачи с помощью генетических алгоритмов
Назад, к списку статей



 Построение полного тестового набора для больших систем вручную очень трудоемко. Существенно снизить затраты на тестирование позволяет автоматизация этого процесса.
Построение полного тестового набора для больших систем вручную очень трудоемко. Существенно снизить затраты на тестирование позволяет автоматизация этого процесса.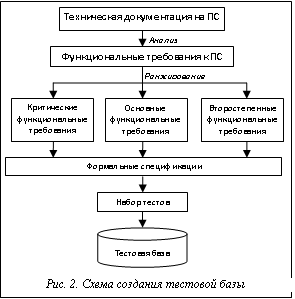 Функция приспособленности должна удовлетворять следующему условию: чем лучше особь, тем выше приспособленность. Наиболее удобно выбрать фитнес-функцию, которая сопоставляет более хорошим особям меньшие значения, так как однозначно понятно, какое решение следует найти. Если предложенное решение удовлетворяет поставленной задаче, его значение приспособленности равно нулю. Если поставленная задача не решена, функция приспособленности оценивает, насколько близок этот вариант к правильному решению задачи. В таком случае цель задачи оптимизации – найти решение с нулевым значением функции приспособленности.
Функция приспособленности должна удовлетворять следующему условию: чем лучше особь, тем выше приспособленность. Наиболее удобно выбрать фитнес-функцию, которая сопоставляет более хорошим особям меньшие значения, так как однозначно понятно, какое решение следует найти. Если предложенное решение удовлетворяет поставленной задаче, его значение приспособленности равно нулю. Если поставленная задача не решена, функция приспособленности оценивает, насколько близок этот вариант к правильному решению задачи. В таком случае цель задачи оптимизации – найти решение с нулевым значением функции приспособленности.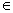 P построить тестовый набор s
P построить тестовый набор s . Элементом тестового покрытия можно считать некий класс событий, которые могут произойти в ходе работы тестируемого ПС. По появлению в процессе исполнения программы элементов тестового покрытия и различных их комбинаций можно судить о полноте или качестве проверки, выполняемой данным тестовым набором. Например, элементами тестового покрытия могут быть исполняемые строки исходного кода (соответствующие событиям их исполнения), ребра графа потока управления, пути в графе потока управления, логические выражения, встречающиеся в исходном коде, и т.п. Кроме того, критерий F определяет логическую функцию
. Элементом тестового покрытия можно считать некий класс событий, которые могут произойти в ходе работы тестируемого ПС. По появлению в процессе исполнения программы элементов тестового покрытия и различных их комбинаций можно судить о полноте или качестве проверки, выполняемой данным тестовым набором. Например, элементами тестового покрытия могут быть исполняемые строки исходного кода (соответствующие событиям их исполнения), ребра графа потока управления, пути в графе потока управления, логические выражения, встречающиеся в исходном коде, и т.п. Кроме того, критерий F определяет логическую функцию  , которая принимает значение f(q, t)=·, если элемент тестового покрытия q покрывается тестом t. Тестовый набор s для системы S удовлетворяет критерию полноты тестового покрытия F, если каждый его элемент из множества
, которая принимает значение f(q, t)=·, если элемент тестового покрытия q покрывается тестом t. Тестовый набор s для системы S удовлетворяет критерию полноты тестового покрытия F, если каждый его элемент из множества  . (1)
. (1)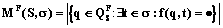 . (2)
. (2)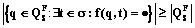 . (3)
. (3)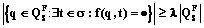 . (4)
. (4)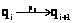 при 1≤i≤n. Упорядоченным подмножеством пути t1, t2, …, tn назовем последовательность, в которой 1£i1
при 1≤i≤n. Упорядоченным подмножеством пути t1, t2, …, tn назовем последовательность, в которой 1£i1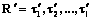 и
и 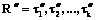 и пусть
и пусть 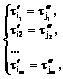 причем 1£i1<
причем 1£i1<