Гидродинамическое описание эволюции исследуемых систем занимает центральное место практически во всех физических приложениях. В качестве примера можно привести конденсированные среды, где в принципе отсутствует кинетический этап эволюции. Гидродинамические исследования в последнее время стимулировали большой поток численных прикладных методов исследований. Гидродинамическое описание конденсированных сред с различным характером упорядочения проникло во все прикладные области современного естествознания – от гидродинамического описания движения жидких кристаллов до сложнейших современных композиционных систем. Оно занимает достаточно большое место в газовой динамике и физике плазмы, позволяет исследовать физическую систему, используя значительно меньшее число степеней свободы.
В среде исследователей различных научных направлений давно существует, как и в технологических отраслях, разделение труда. Однако многим из них, например математикам-прикладникам, часто приходится перемещаться из одной области исследований в смежную область, перенося развитые численные методы на новые технологические области, в которых часто используется современное гидродинамическое описание. Исследование всего класса гидродинамических явлений невозможно без адекватных математических моделей, которые неизбежно проходят через стадию построения системы дифференциальных уравнений, адекватно отображающих физический процесс. Сконструировать необходимую систему дифференциальных уравнений, позволяющую корректно описать интересующее явление, зачастую под силу только экспертам в данной области физических исследований.
Работу такого рода исследователей гидродинамических явлений могла бы значительно облегчить автоматизированная система поддержки, позволяющая правильно выписать систему уравнений, соответствующую требованиям пользователя. Принципиальная возможность развития такой системы поддержки заложена в основных свойствах и характере описания гидродинамического этапа эволюции физических систем. Все вышесказанное делает актуальной проблему автоматизации построения систем дифференциальных уравнений, описывающих гидродинамические системы.
В статье предлагается подход к автоматизации конструирования гидродинамических моделей, развитый в рамках создания системы поддержки конструирования гидродинамических моделей. Система поддержки является экспертной, в режиме диалога с пользователем составляет качественное описание гидродинамической системы и на его основе однозначно строит математическую модель. База знаний системы содержит правила построения качественных моделей и систем дифференциальных уравнений, а рабочая память – конструируемую гидродинамическую модель.
Процесс создания модели гидродинамического явления делится на два этапа: 1) создание качественной модели явления, определяющей количество скоростей и термодинамических степеней свободы, учитываемые физические взаимодействия и другие признаки, характеризующие гидродинамическую систему; 2) создание математической модели, представляющей собой систему дифференциальных уравнений в дивергентной форме (построение математической модели невозможно без построения качественной).
Важной особенностью гидродинамических систем является то, что после определения свойств качественной модели математическая модель строится однозначно, пользователь может задавать только функции зависимости друг от друга некоторых участвующих в уравнениях величин и граничные условия. Сами дифференциальные уравнения, составляющие математическую модель, выводятся из основного термодинамического тождества и законов сохранения массы, энтропии, энергии и импульса, записанных в дивергентной форме.
Такая особенность гидродинамических систем позволяет уточнить понятие качественной модели: в нее входит вся информация, необходимая для однозначного построения системы дифференциальных уравнений.
Реализация подхода в экспертной системе
Целью работы системы поддержки конструирования гидродинамических моделей является сопровождение пользователя при создании модели конкретной гидродинамической системы от неформального замысла до построения системы дифференциальных уравнений в дивергентной форме.
Работа системы осуществляется следующим образом. Пользователь при помощи специального интерфейса в режиме диалога с системой создает качественную модель гидродинамического явления. Диалог организован в форме опроса пользователя системой, в ходе которого пользователь определяет черты и свойства гидродинамической модели, выбирая один из нескольких предлагаемых ответов на вопрос системы. Система ведет опрос пользователя, задавая вопросы и предлагая варианты ответов с учетом уже определенных черт модели. Разработанная последовательность вопросов позволяет системе поддержки провести пользователя через процесс определения всех свойств гидродинамической модели, необходимых для исчерпывающего описания качественной модели. Эта модель описывает физическое приближение, в котором рассматривается явление, и определяет его свойства: количество скоростей и компонент сплошной среды, классификацию компонентов (жидкости, газы или частицы), учитываемые виды физических взаимодействий (гравитационные, электромагнитные) и пр. Качественная модель включает все то, что необходимо для однозначного построения системы дифференциальных уравнений, описывающих рассматриваемое пользователем гидродинамическое явление. На основе этой модели система, используя базу знаний, строит математическую модель явления, которая представляет собой систему дифференциальных уравнений с начальными и граничными условиями. Окончательным результатом работы системы является полностью определенная система дифференциальных уравнений, записанных в дивергентной форме.
Разработанная система поддержки является экспертной системой продукционного типа: она состоит из пользовательского интерфейса, рабочей памяти, базы знаний и машины логического вывода [1]. Для представления знаний в системе используется онтология гидродинамических моделей. Онтология содержит понятия (термины) и отношения, в которых выражены знания о гидродинамических моделях и их конструировании. Рабочая память хранит связанные отношениями экземпляры классов онтологии, описывающие качественную и математическую модели. База знаний содержит оперативные знания из области экспертизы системы, выраженные в терминах онтологии и организованные в виде продукционных правил. Правила анализируют содержащуюся в рабочей памяти качественную модель на предмет полноты и непротиворечивости, управляют диалогом с пользователем и строят математическую модель (систему дифференциальных уравнений) по качественной модели.
Основные физические свойства гидродинамических моделей
Обоснуем физически то, что каждой гидродинамической модели можно сопоставить уникальную качественную модель.
Прежде исследуем факторы, однозначно определяющие систему гидродинамических уравнений.
Первое начало термодинамики для единицы объема сплошной среды имеет вид dE0=dQ+dA.
При условии локального термодинамического равновесия в системе количество получаемого единицей объема среды тепла dQ принимает универсальный вид dQ=TdS, в то время как совершенная над системой работа dA определяется независимыми термодинамическими степенями свободы Yi: dA=X1dY1+…+XndYn.
Таким образом, полное изменение внутренней энергии имеет вид dE0=TdS+X1dY1+…+XndYn, где E0 – внутренняя энергия; S – энтропия единицы объема; T – температура.
Существенное свойство гидродинамического описания состоит в том, что вид первого начала термодинамики, с точки зрения участвующих в нем слагаемых, детерминирует всю систему дифференциальных уравнений, описывающих сплошную среду, для которой первое начало записано. Это вытекает из условия согласования законов сохранения массы, энтропии, импульса и энергии с первым началом термодинамики, которое диктуется необходимостью тождественного выполнения принципа локального термодинамического равновесия [2–4].
Сказанное проиллюстрируем двумя примерами вывода гидродинамической системы уравнений методом термодинамического согласования законов сохранения.
Пример 1 (система уравнений Эйлера). Зададим первое начало термодинамики для жидкости:
dE0=TdS+mdr, (1)
где E0, S – внутренняя энергия и энтропия единицы объема; T – температура; m – химический потенциал; r – плотность жидкости. Плотность и энтропия, входящие в (1), как аддитивные по пространству величины в идеальном гидродинамическом описании удовлетворяют законам сохранения
 , (2)
, (2)
 . (3)
. (3)
Уравнения (2) и (3) отражают в дифференциальной форме то, что аддитивная величина в выделенном объеме может измениться только за счет потоков через границы объема. Закону сохранения должна удовлетворять плотность импульса ji=rvi:
¶tji+¶k(rvivk–pik)=0, (4)
где (rvivk–pik) – тензор плотности потока импульса. Физическое содержание уравнения (4), как и всей системы уравнений Эйлера, определяется конкретным видом этого тензора, который можно получить, не привлекая дополнительную информацию, согласовав законы сохранения с первым началом. Для этого заметим, что полная энергия представляется суммой кинетической и внутренней энергий:
E=E0(S, r)+rv2/2. (5)
Дифференцируем (5) по времени и, воспользовавшись соответствующими законами сохранения, приведем полученное выражение к виду

Закон сохранения энергии 
 , p= –E0+TS+rm, выполняется тождественно, если правая часть равна нулю, то есть при условии pik= –pdik. Таким образом, определился тензор плотности потока импульса rvivk–pdik, который, в свою очередь, определяет плотность силы Ñp/r, действующей на единицу объема жидкости. Последнее легко заметить, если закону сохранения импульса придать форму уравнения движения Эйлера:
, p= –E0+TS+rm, выполняется тождественно, если правая часть равна нулю, то есть при условии pik= –pdik. Таким образом, определился тензор плотности потока импульса rvivk–pdik, который, в свою очередь, определяет плотность силы Ñp/r, действующей на единицу объема жидкости. Последнее легко заметить, если закону сохранения импульса придать форму уравнения движения Эйлера:
¶tvi+vk¶kvi=–¶ip/r. (6)
Таким образом, система уравнений (2)–(4) замкнулась. Рассматриваемая система определена первым началом термодинамики (1) и скоростью vi для описания поля гидродинамических ско- ростей (в данном случае одно поле скоростей). Входящие в первое начало термодинамики аддитивные величины удовлетворяют законам сохранения, что является сутью гидродинамического описания. Показано, что этого достаточно для однозначного определения физического содержания системы – тензора плотности потока импульса:
 ,
,  ,
,
¶tji+¶k(rvivk+pdik)=0.
Пример 2 (электрогидродинамика поляризующихся сред). Проиллюстрируем результаты вывода системы уравнений методом согласования законов сохранения с первым началом на примере электрогидродинамики поляризующихся сред. Объединение электродинамики и гидродинамики проводящей жидкости выполнено с точностью до v2/c2, где c – электродинамическая постоянная; v – скорость гидродинамического течения. Термодинамика электропроводящей жидкости с поляризацией (диэлектрики с утечкой) представляется восьмипараметрической термодинамической системой [4]:
 . (7)
. (7)
Здесь две термодинамические степени имеют, как и в системе уравнений Эйлера, скалярную природу, а две другие – векторную, обусловленную электродинамикой. Внутреннюю энергию можно рассматривать как полную энергию тела в системе отсчета, связанной с движением жидкой частицы. Введенные векторы электрической и магнитной поляризации  относятся к неподвижной системе. Электрическое поле
относятся к неподвижной системе. Электрическое поле  и магнитное поле
и магнитное поле 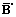 связаны c соответствующими векторами поляризации известными соотношениями
связаны c соответствующими векторами поляризации известными соотношениями  . Связь электромагнитного поля и поляризационных векторов с лабораторной системой отсчета определяется формулами Минковского:
. Связь электромагнитного поля и поляризационных векторов с лабораторной системой отсчета определяется формулами Минковского:


 , (8)
, (8)


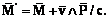
В работе [4] показано, что первое начало термодинамики (7) и уравнения Максвелла
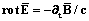 ,
,  ,
,
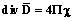 ,
, 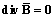 ,
,
в которых плотность тока je и плотность стороннего электрического заряда c, однозначно определяют гидродинамическую систему уравнений:

 ,
,
 ,
,



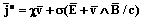 .
.
Можно привести много других примеров гидродинамических систем (жидкие кристаллы, многокомпонентные растворы и т.д.), но общая закономерность сохранится: гидродинамическая система однозначно определяется заданием первого начала термодинамики и количеством скоростей, необходимых для введения гидродинамического описания.
Основы для построения качественной модели
Итак, система дифференциальных уравнений, являющаяся математической моделью сплошной среды, полностью определяется видом первого начала термодинамики и количеством скоростей. В записи первого начала термодинамики для конкретной гидродинамической системы каждый член суммы различной тензорной размерности, за исключением члена TdS, характеризует отдельную черту данной системы. Наличие или отсутствие этого слагаемого означает решение исследователя учитывать соответствующий ему эффект или определять те или иные свойства компонент гидродинамической системы (фазу, тип жидкого кристалла, количество примесей к несущим компонентам).
Определение количества скоростей и вида первого начала термодинамики при работе с гидродинамической системой является той стадией, на которой исследователь переходит от качественных представлений к математическим формулам. С точки зрения автоматизации конструирования гидродинамических моделей такое открытие чрезвычайно важно: во-первых, оно доказывает, что для любой гидродинамической модели и ее системы уравнений существует набор однозначно характеризующих ее качественных утверждений; во-вторых, указывает способ обнаружения данных утверждений – это те и только те утверждения, которые влияют на состав первого начала термодинамики для настоящей системы.
Задача автоматизации конструирования моделей сплошных сред, таким образом, сводится к выделению всех качественных характеристик сплошных сред, определяющих членов первого начала, и к созданию аппарата для работы с ними. Такой аппарат включает информационные объекты, представляющие качественные характеристики, механизм построения целостной качественной модели из объектов и способ построения систем уравнений по качественным моделям.
Качественная модель
Введение качественной модели как способа описания гидродинамической системы является нововведением, необходимость которого вызвана попыткой автоматизации построения математической модели исследуемой пользователем гидродинамической системы. Характер качественной модели, составляющих ее элементов и способа построения определяются спецификой качественных свойств, детерминирующих первое начало термодинамики и поле скоростей сплошной среды, а также предъявляемыми к системе поддержки требованиями и характером ее функционирования.
Существенной особенностью системы поддержки является то, что она работает в диалоговом режиме. Диалог принимает форму опроса пользователя системой, в ходе которого система задает вопросы и предлагает конечное множество вариантов ответа. Опрос движется от общих вопросов к частным, уточняя все более мелкие черты исследуемой гидродинамической системы. Множество вопросов и возможных вариантов ответа сокращается по мере определения характеристик гидродинамической системы, так как уже определенные свойства накладывают ограничения на то, какими могут быть оставшиеся. Опрос продолжается до тех пор, пока не будет построена качественная модель, после чего по ней без участия пользователя будет построена математическая модель (система дифференциальных уравнений). Такой характер работы системы обусловлен непрофессионализмом потенциального пользователя в составлении гидродинамических моделей. Это ведет к тому, что инициатива при построении модели должна принадлежать экспертной системе: она направляет процесс построения качественной модели, определяя вопросы (и их порядок) и множества допустимых ответов. Как вопросы, так и ответы носят качественный характер, избавляя пользователя от ввода формул или иной сложной информации. Такой подход гарантирует надежность системы, защищает от ввода бессмысленной или физически неправильной информации об исследуемой сплошной среде.
Описанному диалоговому характеру построения качественной модели наиболее удовлетворяет модель, состоящая из конечного числа дискретных элементов, так как ее свойства и части определяются по шагам. Элементы модели обладают конечным числом атрибутов, значения которых определяются в ходе диалога. Значения атрибутов также дискретные: это либо целые числа, либо текстовые строки из конечного множества, либо строки, вводимые пользователем как имена частей гидродинамической системы.
Целесообразность использования дискретных элементов подтверждает и природа зависимости систем дифференциальных уравнений от перво- го начала термодинамики: изменяющаяся часть первого начала термодинамики составляется из слагаемых, каждое из которых отражает самостоятельное, не зависящее от других физическое свойство системы, следовательно, целесообразно собирать качественную модель соответствующей гидродинамической системы из дискретных элементов, соответствующих этим свойствам, как из деталей конструктора.
Исследование качественных свойств гидродинамических систем позволило выделить набор фундаментальных свойств, определяющих состав первого начала термодинамики, а следовательно, качественную модель. Для их описания введем ряд понятий.
Компонентой сплошной среды назовем такую ее часть, для описания поведения которой в гидродинамических уравнениях вводится плотность. При моделировании в сплошной среде в качестве разных компонент выделяют субстанции, неоднородные с другими частями среды с точки зрения химических свойств, характера движения, электрического заряда и т.д. Приведем примеры. Если в гидродинамической модели учитываются химические реакции между разными веществами, каждое участвующее в уравнении реакции вещество рассматривается как отдельная компонента со своей собственной плотностью. Если при моделировании учитываются электромагнитные взаимодействия между положительно и отрицательно заряженными частицами среды, частицы с зарядами одного знака рассматриваются как принадлежащие двум разным компонентам.
Компоненты сплошной среды разделим на два класса – независимые и примеси. Независимыми будем называть компоненты, имеющие собственную скорость. Две разные независимые компоненты имеют разные функции скоростей, описывающих их движение в каждой точке сплошной среды, то есть они движутся независимо друг от друга. Компоненты, частицы которых увлекаются независимыми компонентами, движутся так же, как увлекающая их компонента, и не имеют собственной скорости в уравнениях. Такие компоненты могут быть только примесями, растворенными в независимых компонентах.
Установлены следующие основные качественные свойства гидродинамических моделей, влияющие на вид первого начала термодинамики:
- учитывается ли в модели диссипация энергии;
- сколько независимых компонент в гидродинамической системе (сколько скоростей используется для описания движения среды);
- каковы фазы независимых компонент;
- если независимая компонента является жидким кристаллом, то какого он типа (смектик, нематик или холистерик);
- есть ли у независимых компонент примеси, если есть, то сколько;
- учитываются ли электромагнитные взаимодействия;
- учитывается ли при электромагнитных взаимодействиях эффект поляризации;
- учитывается ли действие на систему внешнего гравитационного поля;
- учитывается ли гравитационное самодействие системы.
Приведенный список качественных свойств неполный, однако этого достаточно для иллюстрации концепции.
Для отражения приведенных черт гидродинамических систем выделим следующие виды элементов, из которых будет конструироваться качественная модель: модель, компонента, взаимодействие. Все качественные свойства модели будут передаваться с помощью комбинаций разного количества этих элементов, задания значений их свойств и установления отношений между элементами. Для использования этого инструментария в программном продукте необходимо формализовать его. В качестве средства формализации элементов качественной модели, их свойств и отношений между ними в данном подходе выбрана онтология. Она использовалась для реализации подхода в экспертной системе поддержки построения гидродинамических моделей. Даль- нейшее описание средств построения качественных моделей будет вестись через призму онто- логии.
Онтология качественной модели
В рамках данного подхода онтология рассматривается как совокупность классов (описывающих понятия рассматриваемой предметной области), отношений (возникающих между сущностями, описываемыми классами), слотов (описывающих различные свойства и атрибуты классов) и ограничений, наложенных на слоты и отношения. Данное определение онтологии наиболее близко к приведенному в [5]. Таким образом, разработка онтологии включает в себя определение классов и отношений, создание иерархии классов (подкласс–надкласс), определение слотов и описание их допустимых значений, наложение ограничений на то, как объекты классов могут связываться отношениями.
Классы онтологии
Модель – рабочая память реализованной системы поддержки всегда содержит только один экземпляр данного класса. Обозначает модель гидродинамической системы. Имеет один слот, определяющий идеальность или диссипативность модели.
Компонента – имеющая плотность субстанция, участвующая в гидродинамической системе. Имеет слот, обозначающий, самостоятельная (независимая) компонента или нет, то есть имеет ли она свою собственную скорость, а также слот, определяющий тип фазы компоненты (пыль, жидкость/газ, твердое тело, жидкий кристалл и т.д.). Еще один слот определяет подтип фазы и используется для определения типа жидкого кристалла (смектик, нематик, холистерик).
Взаимодействие обозначает учитываемый в данной модели вид физических взаимодействий. Не имеет слотов. Абстрактный класс, не имеет экземпляров.
Подклассы класса «взаимодействие» являются конкретными; их экземпляры добавляются в модель для обозначения учета различных видов взаимодействий:
- электромагнетизм – учитывается действие на систему внутренних и внешних электромагнитных сил;
- поляризация – учитывается эффект поляризации, возникающий под действием электромагнитных сил;
- самогравитация – учитывается гравитационное взаимодействие частей системы;
- внешнее гравитационное поле – учитывается действие на систему внешнего гравитационного поля;
- химическая реакция – учитываются химические реакции между компонентами системы.
Величина – физическая величина, характеризующая гидродинамическую систему. Имеет слот, содержащий символьное обозначение величины, что позволяет дать конкретным экземплярам подклассов уникальные символьные обозначения, которые войдут в уравнения. Абстрактный класс.
Гидродинамическая величина, термодинамическая величина – абстрактные подклассы класса «величина». Приведем некоторые их конкретные подклассы:
- плотность – плотность компоненты;
- концентрация – плотность компоненты, являющейся примесью;
- скорость – скорость независимой компоненты;
- химпотенциал, давление – характеристики компоненты;
- температура, энтропия – соответствующие термодинамические величины, характеризующие всю гидродинамическую систему как целое;
- вязкость – кинетический коэффициент, характеризующий трение компоненты о саму себя; вязкостью обладают только самостоятельные компоненты; в зависимости от природы компоненты (жидкость, газ, жидкий кристалл и т.д.) она обладает несколькими коэффициентами вязкости (жидкость, к примеру, обладает вязкостью всестороннего сжатия и вязкостью плоскопараллельного сдвига; разные типы вязкости будут представлены разными подклассами);
- коэффициент трения – сила трения между разными независимыми компонентами.
Отношения онтологии
Отношение принадлежности – основное отношение, используемое при построении модели, связывает объект с объектом, который он характеризует. Компоненты, взаимодействия, температура и энтропия связываются с моделью, которую они характеризуют, отношениями принадлежности. Все величины, кроме температуры и энтропии, связываются отношениями принадлежности с теми компонентами, которые они характеризуют. Компоненты-примеси связываются этим отношением с компонентами-носителями, в которых они растворены.
Отношение превращения: если в модели учитываются химические реакции, то компоненты, которые превращаются друг в друга, связываются отношениями превращения.
Проиллюстрируем принципы построения качественной модели с помощью представленной выше онтологии. На рисунке изображена качественная модель гидродинамической системы со следующими свойствами: идеальное приближение; две независимые компоненты (две скорости), одна из которых является жидкостью, другая жидким кристаллом (смектиком) и имеет три примеси; учитываются электромагнитные взаимодействия, эффект поляризации, действие внешнего гравитационного поля и гравитационное самодействие системы. Вершинами обозначены экземпляры классов, дугами – отношения принадлежности, квадратами – свойства экземпляров классов.
 Обобщая сказанное, можно отметить, что в статье описана экспертная система, для которой разработан предлагаемый подход к автоматизации построения моделей. Обнаружены факторы, детерминирующие гидродинамические уравнения: показано, что вид первого начала термодинамики и количество скоростей для сплошной среды однозначно определяют систему дифференциальных уравнений, описывающих данную среду. Факторы, определяющие систему дифференциальных уравнений гидродинамической модели, можно сформулировать в виде качественных свойств этой модели. Перечислены качественные свойства, фундаментальные для построения модели. В целях автоматизации построения моделей сплошных сред совокупность качественных свойств может быть представлена как качественная модель. Показано, что требованиям разработанной экспертной системы и особенностям гидродинамических моделей наиболее соответствует качественная модель, состоящая из дискретных элементов, которые, в свою очередь, обладают набором конечнозначных свойств. Элементы, их свойства и отношения формализованы в виде онтологии. Описаны основные классы и отношения онтологии, разработанной для представления качественных моделей в реализованной экспертной системе поддержки конструирования гидродинамических моделей.
Обобщая сказанное, можно отметить, что в статье описана экспертная система, для которой разработан предлагаемый подход к автоматизации построения моделей. Обнаружены факторы, детерминирующие гидродинамические уравнения: показано, что вид первого начала термодинамики и количество скоростей для сплошной среды однозначно определяют систему дифференциальных уравнений, описывающих данную среду. Факторы, определяющие систему дифференциальных уравнений гидродинамической модели, можно сформулировать в виде качественных свойств этой модели. Перечислены качественные свойства, фундаментальные для построения модели. В целях автоматизации построения моделей сплошных сред совокупность качественных свойств может быть представлена как качественная модель. Показано, что требованиям разработанной экспертной системы и особенностям гидродинамических моделей наиболее соответствует качественная модель, состоящая из дискретных элементов, которые, в свою очередь, обладают набором конечнозначных свойств. Элементы, их свойства и отношения формализованы в виде онтологии. Описаны основные классы и отношения онтологии, разработанной для представления качественных моделей в реализованной экспертной системе поддержки конструирования гидродинамических моделей.
Литература
1. Джарратано Дж., Райли Г. Экспертные системы: принципы разработки и программирование. Изд. 4-е. М.: Издат. дом «Вильямс», 2007.
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: учеб. пособие. М.: Наука, 1988. Т. 6.
3. Blokhin A.M., Dorovsky V.N. Mathematical Modeling in the Theory of Multivelocity Continuum. NY: Nova Science Publishers Inc., 1995.
4. Доровский В.Н., Доровский С.В. О возможностях электроразведки при исследовании устойчивости водонефтяных слоистых систем // Геология и геофизика. 2006. Т. 47. № 7.
5. Ontology Development 101: A Guid to Creating Your First Ontology // Protégé. URL: http://protege.stanford.edu/publications/ontology_development/ontology101-noy-mcguinness.html (дата обращения: 31.08.2011).



 , (2)
, (2) . (3)
. (3)

 , p= –E0+TS+rm, выполняется тождественно, если правая часть равна нулю, то есть при условии pik= –pdik. Таким образом, определился тензор плотности потока импульса rvivk–pdik, который, в свою очередь, определяет плотность силы Ñp/r, действующей на единицу объема жидкости. Последнее легко заметить, если закону сохранения импульса придать форму уравнения движения Эйлера:
, p= –E0+TS+rm, выполняется тождественно, если правая часть равна нулю, то есть при условии pik= –pdik. Таким образом, определился тензор плотности потока импульса rvivk–pdik, который, в свою очередь, определяет плотность силы Ñp/r, действующей на единицу объема жидкости. Последнее легко заметить, если закону сохранения импульса придать форму уравнения движения Эйлера: . (7)
. (7) относятся к неподвижной системе. Электрическое поле
относятся к неподвижной системе. Электрическое поле  и магнитное поле
и магнитное поле 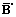 связаны c соответствующими векторами поляризации известными соотношениями
связаны c соответствующими векторами поляризации известными соотношениями  . Связь электромагнитного поля и поляризационных векторов с лабораторной системой отсчета определяется формулами Минковского:
. Связь электромагнитного поля и поляризационных векторов с лабораторной системой отсчета определяется формулами Минковского:

 , (8)
, (8)

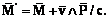
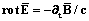 ,
,  ,
,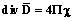 ,
, 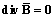 ,
,
 ,
, ,
,


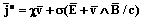 .
.
