Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программная реализация универсального метода исследования устойчивости деформируемых систем в Maple
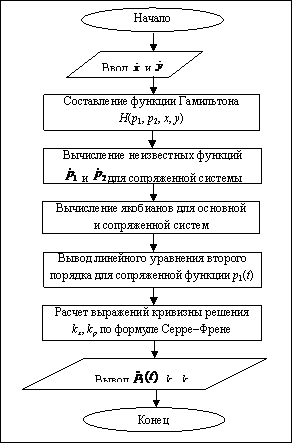
Аннотация:Представлена программа для исследования устойчивости решения нелинейной системы. Разработанная про-грамма позволяет составить функцию Гамильтона, вычислить якобианы для основной и сопряженной систем, найти точки положений равновесия решения, вывести линейное уравнение второго порядка для сопряженной функции, а также рассчитать выражения кривизны решения.
Abstract:The main idea of the article is to present to the readers the program for researching the stability of the decision of nonlinear system. The developed program allows to make function of Hamilton, to calculate Jacobian for the basic and interfaced systems, to find points of positions of balance of the decision, to deduce the linear equation of the second order for the interfaced function, and also to calculate expressions of curvature of the decision.
| Автор: Чусова Е.В. (lioness@pop3.ru) - Тверской государственный университет | |
| Ключевые слова: блок-схема, программная реализация, универсальный метод, устойчивость |
|
| Keywords: flowchart, program realization, universal method, stability |
|
| Количество просмотров: 11521 |
Версия для печати Выпуск в формате PDF (5.33Мб) Скачать обложку в формате PDF (1.08Мб) |
Теория устойчивости движения и равновесия механических систем устанавливает признаки, позволяющие судить об устойчивости рассматриваемого движения или равновесия. Актуальной проблемой теории устойчивости является создание строгих и эффективных методов исследования устойчивости движения систем с распределенными параметрами, особенно сплошных сред. С появлением персональных компьютеров и мощных математических программ cтало возможным решать сложные задачи за короткое время, в том числе исследовать динамическую устойчивость деформируемых систем. В настоящей статье представлена программная реализация исследования устойчивости решения нелинейных систем в программе Maple 12, причем для исследования динамической устойчивости деформируемых систем используется новый метод, предложенный в работе [1], без введения функций Ляпунова. Суть данного метода в следующем. На начальном этапе исходная система дифференциальных уравнений с помощью метода Бубнова–Галеркина приводится к дифференциальному уравнению второго порядка, а затем полученное уравнение сводится к нелинейной системе. Далее составляется функция Гамильтона, которая представляет собой скалярное произведение вектора сопряженных фазовых координат n-мерного из En*-эвклидова сопряженного к En пространства на вектор f(x(t)) функций правых частей исследуемой системы обыкновенных дифференциальных уравнений и пространства En, то есть H=H(x(t), p(t))=(p(t), f(x(t))). Выписывая сопряженную систему обыкновенных дифференциальных уравнений относительно неизвестных функций pi(t), i=1, 2, …, n, по формуле Далее рассчитываются якобианы основной
Если якобиан основной системы неотрицательно определен (отсутствуют положения равновесия типа седла), то решение этой системы устойчиво по Ляпунову, при этом решение сопряженной всегда линейной системы в некоторый произвольно взятый момент времени неустойчиво по критерию Гурвица. В заключение выписываются выражения кривизны решений по формуле Серре–Френе, при этом только для расчета kx результат вычисления умножается на минус единицу:
Необходимо учитывать, что значения кривизны решений должны быть противоположны по знаку. В результате устанавливаются важные фундаментальные факты: - условиями существования функции Ляпунова являются неотрицательная определенность якобиана, неустойчивость решения линейной сопряженной системы и для нелинейной (а также линейной) основной системы – положительность кривизны интегральной кривой; - если решение сопряженной линейной системы орбитально устойчиво, такую же устойчивость имеет и решение основной системы; направления движения по орбитам в фазовых пространствах En и En* противоположны [1]. Данный метод составляет основу для развития специального направления теории и критериев устойчивости нелинейных автономных и неавтономных динамических систем без введения функции Ляпунова. Именно поэтому была составлена программа в Maple 12 на основе универсального метода, которая позволяет выяснить устойчивость решения заданной деформируемой нелинейной системы. Блок-схема программы приведена на рисунке. Алгоритм программы следующий: with(LinearAlgebra); px := y; py := (lambda*(Pi*n)^2-(Pi*n)^4)*x; Выясним, устойчиво ли решение нелинейной системы; dx(t)/dt = px; dy(t)/dt = py; Составим для этого функцию Гамильтона; H(p[1], p[2], x, y) = p[1]*px+p[2]*py; и выпишем сопряженную систему; pp[1] := -(diff(p[1]*px+p[2]*py, x)); pp[2] := -(diff(p[1]*px+p[2]*py, y)); d*p[1]/dt = pp[1]; d*p[2]/dt = pp[2];
J1 := Matrix([[diff(px, x), diff(px, y)], [diff(py, x), diff(py, y)]]); Determinant(J1); J2 := Matrix([[diff(pp[1], p[1]), diff(pp[1], p[2])], [diff(pp[2], p[1]), diff(pp[2], p[2])]]); Determinant(J2); Соответственно для основной и сопряженной системы они не равны нулю, при; Determinant(J1) <> 0; точки положений равновесия решения существуют, если; Determinant(J1) > 0; Преобразуем сопряженную систему в уравнение второго порядка относительно функции p[1](t); pp[1] := subs(p[1] = p[1](t), p[2] = p[2](t), -(diff(p[1]*px+p[2]*py, x))); pp[2] := subs(p[1] = p[1](t), p[2] = p[2](t), -(diff(p[1]*px+p[2]*py, y))); a := d*p[1](t)/dt-pp[1]; d^2*p[1]/dt^2 = subs(diff(p[2](t), t) = pp[2], diff(p[1](t), t) = pp[1], p[2](t) = solve(a, p[2]), diff(pp[1], t)); px := subs(x = x(t), y = y(t), px); py := subs(x = x(t), y = y(t), py); Выражения кривизны решений выписываются по формуле Серре-Френе соответственно в виде; k[x] = -subs(diff(x(t), t) = px, diff(y(t), t) = py, (px*(diff(py, t))-py*(diff(px, t)))/(px^2+ +py^2)^(3/2)); k[p] = subs(diff(p(t), t) = pp[1], diff(p[2](t), t) = pp[2], (pp[1]*(diff(pp[2], t))-pp[2](diff(pp[1], t)))/(pp[1]^2+pp[2]^2)^(3/2)) Для наглядности приведем несколько примеров, а также сопоставим результаты с расчетами, полученными без использования данной программы. Рассмотрим исследование динамической устойчивости центрально сжатого стержня. Дифференциальные уравнения имеют вид w,xxxx+lw,xx+ +w,tt=0, xÎ(0; 1) при граничных условиях w=w,xx=0. В работе [2] данные уравнения были сведены к системе
В результате решения поставленной задачи в программе было получено: - якобианы равны, точки положений равновесия решений существуют при –(l×(pn)2+(pn)4)>0; - линейное уравнение второго порядка для сопряженной функции p1(t) имеет вид - значения кривизны решения для основной и сопряженной систем противоположны по знаку. Полученные результаты хорошо согласуются с вычислениями, проведенными в работе [2]. Рассмотрим исследование динамической устойчивости цилиндрической оболочки под действием внешнего давления. Дифференциальные уравнения взяты в следующем виде:
где В работе [3] данные уравнения были сведены к системе
Путем исследования поставленной задачи в программе было получено: - якобианы для основной и сопряженной систем равны, точки положений равновесия решений существуют при
- линейное уравнение второго порядка для сопряженной функции
- значения кривизны решения для основной и сопряженной систем противоположны по знаку. Данный вывод полностью согласуется с расчетами, проведенными в работе [3]. Настоящая программа была применена в медицине для исследования процесса взаимодействия клеток опухоли и химиотерапевтического средства, которое задается уравнениями [4]
где В результате было получено: - якобианы равны, точки положений равновесия решений существуют при
- линейное уравнение второго порядка для сопряженной функции
- значения кривизны решения для основной и сопряженной систем противоположны по знаку. Данный вывод полностью согласуется с полученными расчетами, проведенными в работе [4]. Таким образом, предлагаемый метод решения уравнения возмущенного движения может быть применен ко всем задачам динамической устойчивости идеальных пластин и оболочек, уравнения которых сводятся к уравнению второго порядка, а разработанная программа позволяет сократить время на решение подобных задач. В заключение следует отметить, что разработанная программа позволяет производить расчеты для определения динамической устойчивости деформируемых систем за короткий промежуток времени. В качестве систем дифференциальных уравнений могут использоваться как автономные механические динамические системы, так и неавтономные. Анализ полученных результатов показывает, что они хорошо согласуются с вычислениями, проведенными ранее вручную. Литература 1. Кудинов А.Н., Катулев А.Н., Кузнецов А.Ю. Исследование устойчивости автономных нелинейных динамических систем // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVI Междунар. симпоз. им. А.Г. Горшкова. М.: МАИ, 2010. С. 110–112. 2. Кудинов А.Н., Чусова Е.В. К исследованию динамической устойчивости деформируемых систем // Синергетика в естественных науках: матер. Междунар. междисциплинар. науч. конф.: Шестые Курдюмовские чтения. Тверь: ТвГУ, 2010. 3. Кудинов А.Н., Чусова Е.В. Исследование динамической устойчивости цилиндрических оболочек // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVII Междунар. симпозиума им. А.Г. Горшкова. М.: 2011. Т. 2. С. 121–134. 4. Кудинов А.Н., Чусова Е.В. Исследование устойчивости процесса взаимодействия клеток опухоли и химиотерапевтического средства // Синергетика в естественных науках: матер. Междунар. междисциплинар. науч. конф.: Седьмые Курдюмовские чтения. Тверь: ТвГУ, 2011. С. 227–229. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3009 |
Версия для печати Выпуск в формате PDF (5.33Мб) Скачать обложку в формате PDF (1.08Мб) |
| Статья опубликована в выпуске журнала № 1 за 2012 год. [ на стр. 36 - 39 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Реализация метода Ляпунова по первому приближению в Maple 12
- Программная реализация цифровой обработки данных силового трансформатора
- Программная реализация математической модели вариативности сердечного ритма
- Управление развитием надежных кластерных структур информационных систем
- Алгоритм и программная реализация имитационной модели гравитационного сепаратора колонного струйно-эмульсионного реактора
Назад, к списку статей



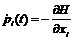 , i=1, 2, …, n, следует учитывать, что данная система всегда линейная однородная с переменными коэффициентами и однозначно сводима к дифференциальному уравнению n-го порядка. Так, для i=1 имеем
, i=1, 2, …, n, следует учитывать, что данная система всегда линейная однородная с переменными коэффициентами и однозначно сводима к дифференциальному уравнению n-го порядка. Так, для i=1 имеем 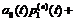
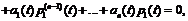 a0(t)¹0, где все коэффициенты непрерывны на области изменения компонент вектора x(t) в n-мерном эвклидовом пространстве En.
a0(t)¹0, где все коэффициенты непрерывны на области изменения компонент вектора x(t) в n-мерном эвклидовом пространстве En.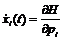 и сопряженной
и сопряженной 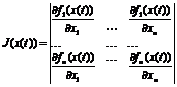 и
и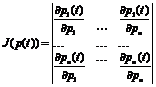 .
.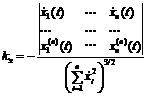 и
и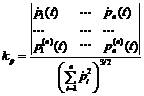 .
. Якобианы основной и сопряженной систем записываются соответственно в виде;
Якобианы основной и сопряженной систем записываются соответственно в виде;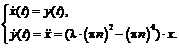
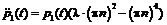 ;
;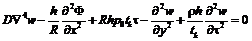 ,
, 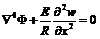 ,
,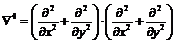 , при этом внешнее давление изменяется по закону p=p0t, p0 – скорость нагружения; F – функция напряжения; r – плотность оболочки; h – толщина стенки оболочки; tk – критическое время; x – осевая координата; y – координата, отсчитываемая в окружном направлении вдоль срединной поверхности.
, при этом внешнее давление изменяется по закону p=p0t, p0 – скорость нагружения; F – функция напряжения; r – плотность оболочки; h – толщина стенки оболочки; tk – критическое время; x – осевая координата; y – координата, отсчитываемая в окружном направлении вдоль срединной поверхности.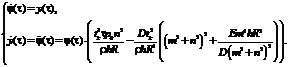
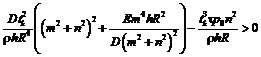 ;
;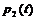 имеет вид
имеет вид
 ,
,  ,
, 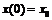 ;
;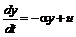 ,
, 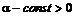 ,
, 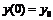 ,
, – функция, описывающая рост числа клеток законом Гомперца.
– функция, описывающая рост числа клеток законом Гомперца. ;
;