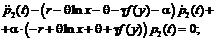Программная реализация универсального метода исследования устойчивости деформируемых систем в Maple
| Чусова Е.В. (lioness@pop3.ru) - Тверской государственный университет | |
| Ключевые слова: блок-схема, программная реализация, универсальный метод, устойчивость |
|
| Keywords: flowchart, program realization, universal method, stability |
|
|
|
|
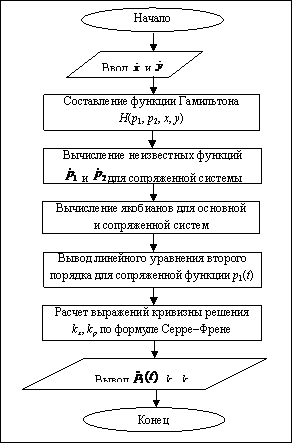
Теория устойчивости движения и равновесия механических систем устанавливает признаки, позволяющие судить об устойчивости рассматриваемого движения или равновесия. Актуальной проблемой теории устойчивости является создание строгих и эффективных методов исследования устойчивости движения систем с распределенными параметрами, особенно сплошных сред. С появлением персональных компьютеров и мощных математических программ cтало возможным решать сложные задачи за короткое время, в том числе исследовать динамическую устойчивость деформируемых систем. В настоящей статье представлена программная реализация исследования устойчивости решения нелинейных систем в программе Maple 12, причем для исследования динамической устойчивости деформируемых систем используется новый метод, предложенный в работе [1], без введения функций Ляпунова. Суть данного метода в следующем. На начальном этапе исходная система дифференциальных уравнений с помощью метода Бубнова–Галеркина приводится к дифференциальному уравнению второго порядка, а затем полученное уравнение сводится к нелинейной системе. Далее составляется функция Гамильтона, которая представляет собой скалярное произведение вектора сопряженных фазовых координат n-мерного из En*-эвклидова сопряженного к En пространства на вектор f(x(t)) функций правых частей исследуемой системы обыкновенных дифференциальных уравнений и пространства En, то есть H=H(x(t), p(t))=(p(t), f(x(t))). Выписывая сопряженную систему обыкновенных дифференциальных уравнений относительно неизвестных функций pi(t), i=1, 2, …, n, по формуле Далее рассчитываются якобианы основной
Если якобиан основной системы неотрицательно определен (отсутствуют положения равновесия типа седла), то решение этой системы устойчиво по Ляпунову, при этом решение сопряженной всегда линейной системы в некоторый произвольно взятый момент времени неустойчиво по критерию Гурвица. В заключение выписываются выражения кривизны решений по формуле Серре–Френе, при этом только для расчета kx результат вычисления умножается на минус единицу:
Необходимо учитывать, что значения кривизны решений должны быть противоположны по знаку. В результате устанавливаются важные фундаментальные факты: - условиями существования функции Ляпунова являются неотрицательная определенность якобиана, неустойчивость решения линейной сопряженной системы и для нелинейной (а также линейной) основной системы – положительность кривизны интегральной кривой; - если решение сопряженной линейной системы орбитально устойчиво, такую же устойчивость имеет и решение основной системы; направления движения по орбитам в фазовых пространствах En и En* противоположны [1]. Данный метод составляет основу для развития специального направления теории и критериев устойчивости нелинейных автономных и неавтономных динамических систем без введения функции Ляпунова. Именно поэтому была составлена программа в Maple 12 на основе универсального метода, которая позволяет выяснить устойчивость решения заданной деформируемой нелинейной системы. Блок-схема программы приведена на рисунке. Алгоритм программы следующий: with(LinearAlgebra); px := y; py := (lambda*(Pi*n)^2-(Pi*n)^4)*x; Выясним, устойчиво ли решение нелинейной системы; dx(t)/dt = px; dy(t)/dt = py; Составим для этого функцию Гамильтона; H(p[1], p[2], x, y) = p[1]*px+p[2]*py; и выпишем сопряженную систему; pp[1] := -(diff(p[1]*px+p[2]*py, x)); pp[2] := -(diff(p[1]*px+p[2]*py, y)); d*p[1]/dt = pp[1]; d*p[2]/dt = pp[2];
J1 := Matrix([[diff(px, x), diff(px, y)], [diff(py, x), diff(py, y)]]); Determinant(J1); J2 := Matrix([[diff(pp[1], p[1]), diff(pp[1], p[2])], [diff(pp[2], p[1]), diff(pp[2], p[2])]]); Determinant(J2); Соответственно для основной и сопряженной системы они не равны нулю, при; Determinant(J1) <> 0; точки положений равновесия решения существуют, если; Determinant(J1) > 0; Преобразуем сопряженную систему в уравнение второго порядка относительно функции p[1](t); pp[1] := subs(p[1] = p[1](t), p[2] = p[2](t), -(diff(p[1]*px+p[2]*py, x))); pp[2] := subs(p[1] = p[1](t), p[2] = p[2](t), -(diff(p[1]*px+p[2]*py, y))); a := d*p[1](t)/dt-pp[1]; d^2*p[1]/dt^2 = subs(diff(p[2](t), t) = pp[2], diff(p[1](t), t) = pp[1], p[2](t) = solve(a, p[2]), diff(pp[1], t)); px := subs(x = x(t), y = y(t), px); py := subs(x = x(t), y = y(t), py); Выражения кривизны решений выписываются по формуле Серре-Френе соответственно в виде; k[x] = -subs(diff(x(t), t) = px, diff(y(t), t) = py, (px*(diff(py, t))-py*(diff(px, t)))/(px^2+ +py^2)^(3/2)); k[p] = subs(diff(p(t), t) = pp[1], diff(p[2](t), t) = pp[2], (pp[1]*(diff(pp[2], t))-pp[2](diff(pp[1], t)))/(pp[1]^2+pp[2]^2)^(3/2)) Для наглядности приведем несколько примеров, а также сопоставим результаты с расчетами, полученными без использования данной программы. Рассмотрим исследование динамической устойчивости центрально сжатого стержня. Дифференциальные уравнения имеют вид w,xxxx+lw,xx+ +w,tt=0, xÎ(0; 1) при граничных условиях w=w,xx=0. В работе [2] данные уравнения были сведены к системе
В результате решения поставленной задачи в программе было получено: - якобианы равны, точки положений равновесия решений существуют при –(l×(pn)2+(pn)4)>0; - линейное уравнение второго порядка для сопряженной функции p1(t) имеет вид - значения кривизны решения для основной и сопряженной систем противоположны по знаку. Полученные результаты хорошо согласуются с вычислениями, проведенными в работе [2]. Рассмотрим исследование динамической устойчивости цилиндрической оболочки под действием внешнего давления. Дифференциальные уравнения взяты в следующем виде:
где В работе [3] данные уравнения были сведены к системе
Путем исследования поставленной задачи в программе было получено: - якобианы для основной и сопряженной систем равны, точки положений равновесия решений существуют при
- линейное уравнение второго порядка для сопряженной функции
- значения кривизны решения для основной и сопряженной систем противоположны по знаку. Данный вывод полностью согласуется с расчетами, проведенными в работе [3]. Настоящая программа была применена в медицине для исследования процесса взаимодействия клеток опухоли и химиотерапевтического средства, которое задается уравнениями [4]
где В результате было получено: - якобианы равны, точки положений равновесия решений существуют при
- линейное уравнение второго порядка для сопряженной функции
- значения кривизны решения для основной и сопряженной систем противоположны по знаку. Данный вывод полностью согласуется с полученными расчетами, проведенными в работе [4]. Таким образом, предлагаемый метод решения уравнения возмущенного движения может быть применен ко всем задачам динамической устойчивости идеальных пластин и оболочек, уравнения которых сводятся к уравнению второго порядка, а разработанная программа позволяет сократить время на решение подобных задач. В заключение следует отметить, что разработанная программа позволяет производить расчеты для определения динамической устойчивости деформируемых систем за короткий промежуток времени. В качестве систем дифференциальных уравнений могут использоваться как автономные механические динамические системы, так и неавтономные. Анализ полученных результатов показывает, что они хорошо согласуются с вычислениями, проведенными ранее вручную. Литература 1. Кудинов А.Н., Катулев А.Н., Кузнецов А.Ю. Исследование устойчивости автономных нелинейных динамических систем // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVI Междунар. симпоз. им. А.Г. Горшкова. М.: МАИ, 2010. С. 110–112. 2. Кудинов А.Н., Чусова Е.В. К исследованию динамической устойчивости деформируемых систем // Синергетика в естественных науках: матер. Междунар. междисциплинар. науч. конф.: Шестые Курдюмовские чтения. Тверь: ТвГУ, 2010. 3. Кудинов А.Н., Чусова Е.В. Исследование динамической устойчивости цилиндрических оболочек // Динамические и технологические проблемы механики конструкций и сплошных сред: матер. XVII Междунар. симпозиума им. А.Г. Горшкова. М.: 2011. Т. 2. С. 121–134. 4. Кудинов А.Н., Чусова Е.В. Исследование устойчивости процесса взаимодействия клеток опухоли и химиотерапевтического средства // Синергетика в естественных науках: матер. Междунар. междисциплинар. науч. конф.: Седьмые Курдюмовские чтения. Тверь: ТвГУ, 2011. С. 227–229. |
http://swsys.ru/index.php?page=article&id=3009&lang=%E2%8C%A9=en |
|
Perhaps, you might be interested in the following articles of similar topics:
- Реализация метода Ляпунова по первому приближению в Maple 12
- Программная реализация цифровой обработки данных силового трансформатора
- Программная реализация математической модели вариативности сердечного ритма
- Управление развитием надежных кластерных структур информационных систем
- Алгоритм и программная реализация имитационной модели гравитационного сепаратора колонного струйно-эмульсионного реактора

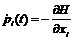 , i=1, 2, …, n, следует учитывать, что данная система всегда линейная однородная с переменными коэффициентами и однозначно сводима к дифференциальному уравнению n-го порядка. Так, для i=1 имеем
, i=1, 2, …, n, следует учитывать, что данная система всегда линейная однородная с переменными коэффициентами и однозначно сводима к дифференциальному уравнению n-го порядка. Так, для i=1 имеем 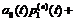
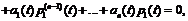 a0(t)¹0, где все коэффициенты непрерывны на области изменения компонент вектора x(t) в n-мерном эвклидовом пространстве En.
a0(t)¹0, где все коэффициенты непрерывны на области изменения компонент вектора x(t) в n-мерном эвклидовом пространстве En.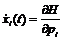 и сопряженной
и сопряженной 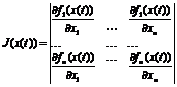 и
и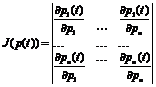 .
.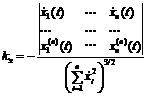 и
и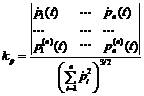 .
. Якобианы основной и сопряженной систем записываются соответственно в виде;
Якобианы основной и сопряженной систем записываются соответственно в виде;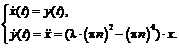
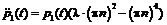 ;
;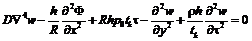 ,
, 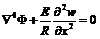 ,
,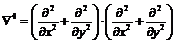 , при этом внешнее давление изменяется по закону p=p0t, p0 – скорость нагружения; F – функция напряжения; r – плотность оболочки; h – толщина стенки оболочки; tk – критическое время; x – осевая координата; y – координата, отсчитываемая в окружном направлении вдоль срединной поверхности.
, при этом внешнее давление изменяется по закону p=p0t, p0 – скорость нагружения; F – функция напряжения; r – плотность оболочки; h – толщина стенки оболочки; tk – критическое время; x – осевая координата; y – координата, отсчитываемая в окружном направлении вдоль срединной поверхности.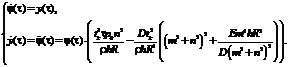
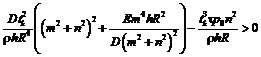 ;
;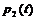 имеет вид
имеет вид
 ,
,  ,
, 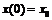 ;
;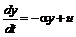 ,
, 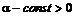 ,
, 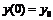 ,
, – функция, описывающая рост числа клеток законом Гомперца.
– функция, описывающая рост числа клеток законом Гомперца. ;
;