Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Аппроксимация эмпирического распределения случайных замеров модифицированным законом Эрланга
Аннотация:
Abstract:
| Автор: Неклюдова С.А. () - | |
| Ключевое слово: |
|
| Ключевое слово: |
|
| Количество просмотров: 14613 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
В практике встречаются попытки решения задачи прогнозирования технического состояния изделия (ТСИ) экстраполяцией ретроспективных наблюдений (по материалам ряда дефектаций) или имитационным моделированием исследуемого процесса в предполагаемых условиях с помощью специально разработанных моделирующих алгоритмов. Проведение вычислительного эксперимента при имитационном моделировании случайного процесса, как правило, базируется на методе статистических испытаний. При этом возникает необходимость установления законов распределения случайных величин как для воспроизводства их реализаций, так и для определения закономерностей показателей, получаемых в результате моделирования.
Большинство элементов изделия эксплуатируется в однородных условиях, и их износ подчиняется нормальному закону. Однако есть элементы, перекрывающие два района (и более) с разными условиями эксплуатации. Это приводит к неравномерному износу элементов. Причем замеры на таких участках располагаются неравномерно: чем больше износ элементов, тем больше на этом участке делают замеров. Указанные особенности обусловили постановку задачи подбора закона распределения, которому следует совокупность экспериментальных данных. По существу это сводится к аппроксимации эмпирического распределения соответствующим теоретическим законом. Один из возможных методов решения данной задачи основан на использовании в качестве аппроксимирующего закона распределения Эрланга. Это позволяет количественно и функционально учесть практически весь диапазон той неравномерности, с которой следуют события (наблюденные значения). В теории вероятностей известны два вида такого распределения – ненормированное и нормированное. Характерной особенностью указанных распределений Эрланга является принятие порядком распределения только целочисленных значений (t=1,2,3,...). В практике математической статистики величина t может принимать любые, в том числе нецелочисленные значения от 0 до бесконечности. С учетом этого предлагается ввести понятие обобщенного нормированного распределения Эрланга, пригодного для любых, в том числе и нецелочисленных значений t. При этом соответствующей заменой переменных обобщенное нормированное распределение Эрланга удалось свести к частному случаю гамма-распределения. Для краткости назовем его просто законом распределения Эрланга, который описывается следующими выражениями: · дифференциальная форма f(t) – плотность вероятности:
· интегральная форма F(t) – функция распределения:
В (1,2) t, Гамма-функция
Неполная гамма-функция
где параметр x в нашем случае принимает значение Введем обозначение
тогда функция распределения (2) принимает вид:
Для вычисления функции (5) существует специальная таблица, а также разработаны алгоритмы, позволяющие рассчитать ее при любых значениях аргументов т, h и t. С целью практического использования закона распределения Эрланга и для оценки вероятностных характеристик совокупности эмпирических данных, являющихся реализациями непрерывной случайной величины, по этим данным необходимо определить следующие числовые характеристики: Для определения оценок
Полученные по зависимостям (7) значения Практическая ценность изложенного метода заключается в возможности использования его для аппроксимации достаточно широкого круга эмпирических распределений, каждое из которых характеризуется своим порядком распределения m. При m=1 – экспоненциальное распределение; при |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=304 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
| Статья опубликована в выпуске журнала № 4 за 2007 год. |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Схемотехнические САПР для персональных компьютеров
- Программная система функционального проектирования аппаратных комплексов АСУТП
- Инструментальные и программные средства построения сетевых моделей
- Сравнительная характеристика текстовых редакторов
- Основы интеллектуальной информационной технологии обеспечения безопасности производства
Назад, к списку статей



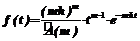 . (1)
. (1)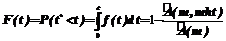 . (2)
. (2) – неслучайная и случайная величины; Р – оператор вероятности;
– неслучайная и случайная величины; Р – оператор вероятности; 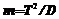 – порядок распределения закона Эрланга (D – дисперсия случайной величины);
– порядок распределения закона Эрланга (D – дисперсия случайной величины); 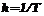 – параметр распределения (Т – математическое ожидание случайной величины).
– параметр распределения (Т – математическое ожидание случайной величины).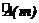 находится по формуле:
находится по формуле: . (3)
. (3)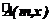 находится по формуле:
находится по формуле: , (4)
, (4)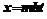 .
.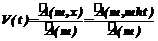 , (5)
, (5)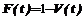 . (6)
. (6) ,
, 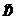 и
и  – оценки математического ожидания, дисперсии и порядка распределения Эрланга соответственно.
– оценки математического ожидания, дисперсии и порядка распределения Эрланга соответственно. ;
;  . (7)
. (7)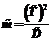 . (8)
. (8) – распределение с дисперсией (неравномерностью) больше, чем в экспоненциальном распределении; при m≈8 – распределение, близкое к нормальному, а при
– распределение с дисперсией (неравномерностью) больше, чем в экспоненциальном распределении; при m≈8 – распределение, близкое к нормальному, а при 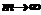 дисперсия убывает до нуля, и распределение стремится к закону единичной функции, характеризующей неслучайную величину.
дисперсия убывает до нуля, и распределение стремится к закону единичной функции, характеризующей неслучайную величину.