Высокие темпы развития пищевой, фармацевтической и косметической промышленности в мире обусловливают необходимость решения разнообразных задач моделирования процессов в этих предметных областях. Одним из важных является процесс растворения твердых тел в различных растворителях при разных условиях.
При растворении твердых тел стоит учитывать ряд факторов, которые могут повлиять на ход процесса растворения, например: твердое тело может состоять из нескольких компонентов, имеющих разную растворимость; оно может быть покрыто оболочкой, затрудняющей растворение, а также иметь несимметричную форму; в состав твердого тела могут входить вещества, способные увеличивать растворимость других входящих в него веществ.
На текущий момент уже существуют разнообразные математические модели растворения твердых тел на основе дифференциальных уравнений (Weibull, Hixon–Crowell, Korsemeyer–Peppas и т.д.).
Данная статья посвящена описанию модели растворения твердых тел на основе вероятностного клеточного автомата. При работе над моделью авторы попытались учесть все факторы, перечисленные выше.
Описание модели клеточного автомата
В основе модели лежит вероятностный клеточный автомат [1]. Клетки автомата образуют прямоугольное поле размером N´N клеток. Модель имеет следующие допущения:
– система представляется в виде поля, состоящего из квадратных клеток;
– каждая клетка имеет четыре соседние клетки;
– поле может быть замкнутым или открытым;
– клеточный автомат является синхронным, то есть считается, что все изменения за одну итерацию происходят в одно и то же время;
– клетка описывается тремя характеристиками – типом вещества, его количеством, находящимся в данной клетке, и агрегатным состоянием («жидкость» или «твердое вещество»);
– в каждой клетке может находиться только одно вещество;
– состояние клетки зависит только от соседних клеток;
– при снижении количества вещества в клетке до уровня, соответствующего концентрации насыщенного раствора этого вещества, состояние клетки переходит в «жидкость»;
– при увеличении количества вещества в клетке до уровня, превышающего концентрацию насыщенного раствора этого вещества, состояние клетки переходит в «твердое вещество»;
– диффузия может происходить только между клетками, имеющими состояние «жидкость».
Клеточный автомат работает итеративно. В начале итерации рассчитываются новые значения клеток, которые принимают значения «раствор вещества» и «твердое вещество». Начиная с клетки с индексом (0, 0), последовательно происходит проверка значения, которое содержится в клетке.
Если значение от 0 до Cнасыщ., значит, клетка имеет состояние «раствор вещества». Для клеток такого типа действуют следующие правила.
Каждая соседняя клетка с состоянием «растворитель» уменьшает значение в клетке на Сp1 (зависящее от коэффициента диффузии, линейного размера клетки и времени одной итерации) за одну итерацию, при этом клетка с состоянием «растворитель» переходит в состояние «раствор вещества» со значением Сp1.
 Каждая соседняя клетка с состоянием «твердое вещество» увеличивает значение в клетке на Ст1 (зависящее от коэффициента растворения, линейного размера клетки и времени одной итерации) за одну итерацию, при этом значение в клетке с состоянием «твердое вещество» уменьшается на Ст1. При достижении значения, большего Cнасыщ., состояние клетки принимается как «твердое вещество».
Каждая соседняя клетка с состоянием «твердое вещество» увеличивает значение в клетке на Ст1 (зависящее от коэффициента растворения, линейного размера клетки и времени одной итерации) за одну итерацию, при этом значение в клетке с состоянием «твердое вещество» уменьшается на Ст1. При достижении значения, большего Cнасыщ., состояние клетки принимается как «твердое вещество».
Если значение в клетке от Cнасыщ. до Cmax, значит, клетка имеет состояние «твердое вещество». Для клеток такого типа действует следующее правило.
Каждая соседняя клетка с состоянием «растворитель» уменьшает значение в клетке на Сp2 (зависящее от коэффициента растворения, линейного размера клетки и времени одной итерации) за одну итерацию, при этом клетка с состоянием «растворитель» переходит в состояние «раствор вещества» со значением Сp2. При достижении значения, меньшего или равного Cнасыщ., состояние клетки принимается как «раствор вещества».
Таким образом, суммарные значения по каждому из веществ в клетках с состоянием «твердое вещество» и «раствор вещества» в процессе расчета не изменяются. Коэффициенты Cнасыщ., Ст1, Сp1, Сp2 определяются исходя из физико-химических величин (коэффициенты диффузии и растворения) и параметров клеточного автомата (линейный размер клетки, время одной итерации). Растворение в данной клеточно-автоматной модели по физическому смыслу схоже с дифферинциальным уравнением растворения твердого тела: где М – изменение массы твердого вещества; k – коэффициент растворения; F – поверхность растворения; Cнасыщ. – концентрация насыщенного раствора.
 После окончания расчета значений для клеток с состоянием «твердое вещество» и «раствор вещества» начинается расчет диффузии. Происходит случайный выбор p процентов пар клеток «раствор вещества»–«растворитель», и в каждой паре значения клеток меняются местами. Таким образом, этап расчета диффузии позволяет предотвратить ситуацию, когда вокруг клеток «твердого вещества» образуется пограничная зона с клетками «раствора вещества».
После окончания расчета значений для клеток с состоянием «твердое вещество» и «раствор вещества» начинается расчет диффузии. Происходит случайный выбор p процентов пар клеток «раствор вещества»–«растворитель», и в каждой паре значения клеток меняются местами. Таким образом, этап расчета диффузии позволяет предотвратить ситуацию, когда вокруг клеток «твердого вещества» образуется пограничная зона с клетками «раствора вещества».
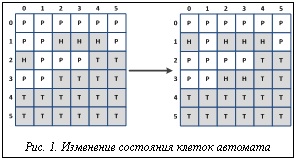
После расчета диффузии начинается следующая итерация. Количество итераций определяет пользователь в начальных настройках. На рисунке 1, где изображена часть поля клеточного автомата, показано изменение состояния автомата через одну итерацию. Как видно из рисунка, клетки с координатами (2, 3) и (3, 3) имели состояние «твердое вещество» (Т) и перешли в состояние «раствор вещества» (Н) (изменение произошло при расчете растворения), а клетки (0, 1) и (0, 2) поменяли свои состояния (расчет диффузии).
Как было показано в допущениях к модели, для данного клеточного автомата предусмотрена работа в режимах с открытыми и замкнутыми границами. При работе в режиме открытых границ в конце каждой итерации границы клеточного автомата (те клетки, которые имеют координату X или координату Y, равную 0 или N) принимают значение «растворитель». Это позволяет моделировать систему растворения твердого тела в объеме жидкости, многократно превышающем объем тела. При работе автомата в режиме замкнутых границ соседней клеткой с клеткой границы считается клетка на противоположной границе поля автомата, то есть для клеток (А, 0) и (0, В) соседними являются (А, N-1) и (N-1, В) соответственно.
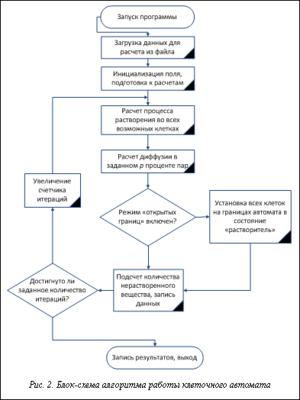
На рисунке 2 приведена блок-схема алгоритма работы программы, реализующей описанный выше клеточный автомат.
Результаты расчета
После разработки клеточного автомата были выполнены расчеты с различными коэффициентами Cнасыщ., Ст1, Сp1, Сp2, p для сравнения с экспериментальными данными.
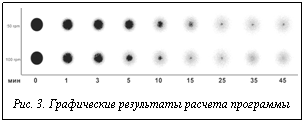 В качестве экспериментальных данных взяты значения концентраций в различное время при растворении таблетки аскорбиновой кислоты. В двух различных экспериментах были выбраны разные обороты лопастной мешалки. На рисунке 3 показаны результаты расчета программы в графическом виде. На фоне растворителя черным цветом отображены ячейки, содержащие нерастворенную аскорбиновую кислоту, серым – раствор аскорбиновой кислоты.
В качестве экспериментальных данных взяты значения концентраций в различное время при растворении таблетки аскорбиновой кислоты. В двух различных экспериментах были выбраны разные обороты лопастной мешалки. На рисунке 3 показаны результаты расчета программы в графическом виде. На фоне растворителя черным цветом отображены ячейки, содержащие нерастворенную аскорбиновую кислоту, серым – раствор аскорбиновой кислоты.
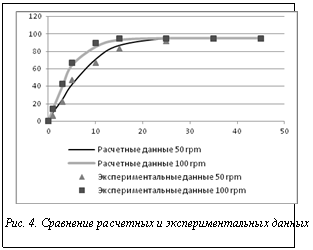
После расчетов было проведено сравнение расчетных и экспериментальных данных. На рисунке 4 приведены расчетные графики и экспериментальные точки. Как видно из результатов, клеточно-автоматная модель хорошо описывает растворение твердого тела в растворителе. Отклонение расчетных данных от экспериментальных составляет не более 5 %.
Программная реализация
Клеточный автомат реализован на языке программирования C# 4.0 на платформе Microsoft .NET Framework 4.0. В программе использованы алгоритмы распараллеливания расчетов Microsoft Parallel [2], что позволяет оптимально использовать всю суммарную вычислительную мощность центральных процессоров компьютера, на котором производится расчет. Кроме реализации клеточного автомата, была разработана программа, позволяющая пользователям задавать параметры с помощью графического интерфейса. На данный момент максимальный размер линейного поля клеточного автомата составляет 1 500 клеток при расчете на компьютере с объемом оперативной памяти 4 GB.
 Дальнейшие работы. Как уже отмечалось, существуют такие проблемы, как многокомпонентность, различные покрытия твердого тела и др. Данная модель позволяет учитывать все вышеперечисленные факторы путем введения новых состояний клеток и, соответственно, новых правил для этих состояний. В ходе дальнейших исследований предполагается провести ряд экспериментов и представить результаты моделирования растворения для различных твердых тел. Кроме того, планируется реализация данного клеточного автомата на языке программирования C/C++ с использованием технологии nVidia CUDA, что позволит проводить параллельные вычисления с использованием ядер графического адаптера компьютера. Применение технологии nVidia CUDA значительно увеличит скорость расчета и даст возможность проводить расчеты полей линейным размером более 10 000 клеток. Применение данной технологии распараллеливания позволит перейти от двухмерной модели к трехмерной, что дает возможность моделировать растворение тел с любой формой.
Дальнейшие работы. Как уже отмечалось, существуют такие проблемы, как многокомпонентность, различные покрытия твердого тела и др. Данная модель позволяет учитывать все вышеперечисленные факторы путем введения новых состояний клеток и, соответственно, новых правил для этих состояний. В ходе дальнейших исследований предполагается провести ряд экспериментов и представить результаты моделирования растворения для различных твердых тел. Кроме того, планируется реализация данного клеточного автомата на языке программирования C/C++ с использованием технологии nVidia CUDA, что позволит проводить параллельные вычисления с использованием ядер графического адаптера компьютера. Применение технологии nVidia CUDA значительно увеличит скорость расчета и даст возможность проводить расчеты полей линейным размером более 10 000 клеток. Применение данной технологии распараллеливания позволит перейти от двухмерной модели к трехмерной, что дает возможность моделировать растворение тел с любой формой.
В заключение отметим, что в данной статье представлены клеточно-автоматная модель растворения твердых тел на примере растворения таблетки аскорбиновой кислоты и ее программная реализация. Отмечено, что процесс растворения твердого тела зависит от многих параметров, в частности, от состава твердого тела, наличия покрытия, среды растворения, температуры среды и других. Рассмотренная клеточно-автоматная модель позволяет учесть при расчете все данные параметры, но с увеличением их количества скорость расчета по представленной модели уменьшается.
Литература
1. Тоффоли Т., Марголус Н. Машины клеточных автоматов; [пер. с англ.]. М.: Мир, 1991. 280 с.
2. URL: http://msdn.microsoft.com/en-us/library/dd460693. aspx (дата обращения: 17.09.2011).



 Каждая соседняя клетка с состоянием «твердое вещество» увеличивает значение в клетке на Ст1 (зависящее от коэффициента растворения, линейного размера клетки и времени одной итерации) за одну итерацию, при этом значение в клетке с состоянием «твердое вещество» уменьшается на Ст1. При достижении значения, большего Cнасыщ., состояние клетки принимается как «твердое вещество».
Каждая соседняя клетка с состоянием «твердое вещество» увеличивает значение в клетке на Ст1 (зависящее от коэффициента растворения, линейного размера клетки и времени одной итерации) за одну итерацию, при этом значение в клетке с состоянием «твердое вещество» уменьшается на Ст1. При достижении значения, большего Cнасыщ., состояние клетки принимается как «твердое вещество».
 В качестве экспериментальных данных взяты значения концентраций в различное время при растворении таблетки аскорбиновой кислоты. В двух различных экспериментах были выбраны разные обороты лопастной мешалки. На рисунке 3 показаны результаты расчета программы в графическом виде. На фоне растворителя черным цветом отображены ячейки, содержащие нерастворенную аскорбиновую кислоту, серым – раствор аскорбиновой кислоты.
В качестве экспериментальных данных взяты значения концентраций в различное время при растворении таблетки аскорбиновой кислоты. В двух различных экспериментах были выбраны разные обороты лопастной мешалки. На рисунке 3 показаны результаты расчета программы в графическом виде. На фоне растворителя черным цветом отображены ячейки, содержащие нерастворенную аскорбиновую кислоту, серым – раствор аскорбиновой кислоты. Дальнейшие работы. Как уже отмечалось, существуют такие проблемы, как многокомпонентность, различные покрытия твердого тела и др. Данная модель позволяет учитывать все вышеперечисленные факторы путем введения новых состояний клеток и, соответственно, новых правил для этих состояний. В ходе дальнейших исследований предполагается провести ряд экспериментов и представить результаты моделирования растворения для различных твердых тел. Кроме того, планируется реализация данного клеточного автомата на языке программирования C/C++ с использованием технологии nVidia CUDA, что позволит проводить параллельные вычисления с использованием ядер графического адаптера компьютера. Применение технологии nVidia CUDA значительно увеличит скорость расчета и даст возможность проводить расчеты полей линейным размером более 10 000 клеток. Применение данной технологии распараллеливания позволит перейти от двухмерной модели к трехмерной, что дает возможность моделировать растворение тел с любой формой.
Дальнейшие работы. Как уже отмечалось, существуют такие проблемы, как многокомпонентность, различные покрытия твердого тела и др. Данная модель позволяет учитывать все вышеперечисленные факторы путем введения новых состояний клеток и, соответственно, новых правил для этих состояний. В ходе дальнейших исследований предполагается провести ряд экспериментов и представить результаты моделирования растворения для различных твердых тел. Кроме того, планируется реализация данного клеточного автомата на языке программирования C/C++ с использованием технологии nVidia CUDA, что позволит проводить параллельные вычисления с использованием ядер графического адаптера компьютера. Применение технологии nVidia CUDA значительно увеличит скорость расчета и даст возможность проводить расчеты полей линейным размером более 10 000 клеток. Применение данной технологии распараллеливания позволит перейти от двухмерной модели к трехмерной, что дает возможность моделировать растворение тел с любой формой.