Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Реализация системы обработки изображений линейчатых объектов
Аннотация:
Abstract:
| Авторы: Орлов А.А. (alexeyalexorlov@gmail.com) - уромский институт (филиал) Владимирского государственного университета им. Александра Григорьевича и Николая Григорьевича Столетовых, г. Муром, Россия, доктор технических наук | |
| Количество просмотров: 9555 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
Для большинства классов изображений наибольшую ценность представляют данные препарата протяженных линейчатых объектов. Таковыми являются, например, контуры на изображениях. По границам (контурам) человек распознает и анализирует форму объектов на рассматриваемой сцене. Сообразно с этим в области компьютерной обработки изображений существует большее количество работ, связанных с выделением и анализом границ (напр.: Методы компьютерной обработки изображений. М.: Физматлит, 2003 и Yin Y., Tian G.Y., Automatic X-Ray Image characterization for Non-Destructive Evaluation, School of Computing and Engineering Researchers’ Conference, University of Huddersfield, Dec 2006). Имеются также сцены, на которых непосредственно присутствуют изображения объектов в виде полос (линейчатых образов). Это изображения рукописей, треков движения объектов и частиц, сварных соединений, ребер на флюорограммах и многое другое. На простых изображениях выделение и анализ таких полосовых объектов (или просто полос) не составляет трудности, но на сложных и малоконтрастных реальных сценах выделяемые объекты разрушены шумом и присутствием других образов. Анализ таких изображений является весьма малоизученной предметной областью: большинство методов данной сферы являются эмпирическими, а некоторые важные ее задачи до сих пор не решены. Актуальным является создание новой математической теории, позволяющей построить алгоритм (связанный с полосовым анализом) для реализации системы обработки линейчатых изображений. Целью работы является создание системы обработки и анализа полосовых растровых образов. Можно показать, что на многих изображениях среднестатистически профиль (срез) яркости полосы на полутоновом изображении аппроксимируется второй производной гауссиана Для анализа таких перепадов яркости будем использовать вэйвлет-преобразование (Малла С. Вэйвлеты в обработке сигналов. М.: Мир, 2005):
где f(t) – профиль функции яркости исходного изображения; s – масштаб, равный полуширине полосы. Коэффициент Для обратного вэйвлет-преобразования используется выражение:
где С – нормирующий множитель; В работе С. Малла (ссылку см. выше) показано, что Фурье-спектр g(t):
Будем полагать, что, интегрируя не от -¥ до +¥, а в промежутке [s1,s2], мы подавляем (фильтруем) перепады с масштабом не из этого промежутка, то есть выделяем перепады яркости с масштабом от s1 до s2. В результате образуется фильтр, подчеркивающий средние частоты, соответствующие [s1,s2]. Обобщим формулы на двухмерный случай. Будем решать задачу выделения полосы, заданной функцией f: R2 ®R. Для этого представим полосу как объект, состоящий из некоторых сегментов. Каждый сегмент аппроксимируем второй производной гауссоида В таком случае фильтрация полосы запишется:
где Обозначим данное преобразование как g(x,y)=F[f(x,y),s1,s2]. Введем интегральное преобразование, учитывающее ориентацию сегмента полосы:
где q – угол поворота поверхности z=y(x,y) вокруг оси аппликат. Введенное выражение назовем интегральным преобразованием по сегменту полосы полушириной [s1, s2]. Таким образом, алгоритм выделения полос будет состоять из двух шагов: 1) формирование функции g(x,y,q); 2) поиск максимальных значений по углам из заданного промежутка [q1 ,q2]. На основе полученной теории на языке программирования С++ разработана система для вы- деления полосовых образов. Созданная система исследовалась на тестовых образах и апробирована на реальных изображениях ребер на флюорограммах, текстах рукописей и дефектоскопических снимках для выделения трещин. Получены хорошие результаты, подтверждающие высокое качество работы алгоритмов системы. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=308 |
Версия для печати Выпуск в формате PDF (2.00Мб) |
| Статья опубликована в выпуске журнала № 4 за 2007 год. |
Назад, к списку статей



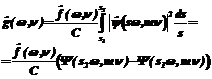 ,
,