Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Программное средство для имитационного моделирования с помощью графовых моделей
Аннотация:Рассмотрены текущая реализация и перспективы развития оригинального программного средства G-IPS Ultimate, предназначенного для имитационного моделирования (в том числе систем реального времени). Модель системы за-дается с помощью набора решающих графов специального вида, которые позволяют строить нечеткие модели систем.
Abstract:We introduce the original program package G-IPS Ultimate intended for simulation modeling of systems (including real-time modeling). The simulation model is represented by set of decision graphs of special kind, which allows to defining a fuzzy models of system. According to the obtained results we made up conclusions on the future development of the proposed methods and the practical application of the software.
| Авторы: Карпухин И.Н. (surstrat@mail.ru) - Российский государственный социальный университет, г. Москва, Кораблин Ю.П. (y.p.k@mail.ru) - Российский государственный социальный университет, г. Москва (профессор), Москва, Россия, доктор технических наук, Незнанов А.А. (aneznanov@hse.ru) - Государственный университет – Высшая школа экономики, г. Москва, кандидат технических наук | |
| Ключевые слова: программный комплекс, продукционные знания, экспертные знания, графовая модель, имитационное моделирование |
|
| Keywords: software package, bases of diagnostic knowledge, expert diagnostic system, graph model, simulation |
|
| Количество просмотров: 12693 |
Версия для печати Выпуск в формате PDF (5.19Мб) Скачать обложку в формате PDF (1.31Мб) |
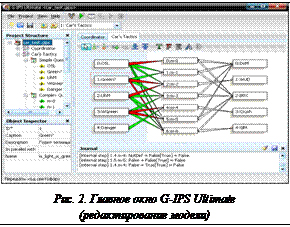
Компьютерное имитационное моделирование (ИМ) систем сегодня является актуальной задачей, а проблема выбора модели описания логики протекания процессов остается открытой. Имитационное моделирование – мощный и зачастую единственно доступный инструмент исследования поведения сложных систем [1]. Методы ИМ позволяют собрать необходимую информацию о поведении системы с помощью вычислительных экспериментов над компьютерной моделью системы, реагирующей на сигналы внешней среды. Актуальность исследования данной задачи обусловлена переходом к автоматизации сложных систем в различных производственных областях, а также важностью прогнозирования поведения процессов во времени. Причинами активного развития ИМ стали кризис аналитичности, когда для многих задач отсутствовали аналитические решения, и появление новых классов задач предсказательного моделирования. Вместо натурного эксперимента имитация может потребоваться по следующим причинам: система недоступна, эксперимент на реальной системе слишком затратен, функционирование системы сопряжено с большими рисками, система еще не существует [2]. Перед моделированием необходимо выбрать модель представления экспертных знаний. В числе наиболее доступных и распространенных – модели на основе продукционных правил. Продукционные модели используются для решения сложных задач, которые основаны на применении эвристических методов представления знаний, позволяющих настраивать механизм вывода на особенности проблемной области в условиях неопределенности. В продукционной модели основной единицей знаний является правило вида: «если <посылка>, то <заключение>», с помощью которого можно выразить пространственно-временные, причинно-следственные, функционально-поведенческие (ситуация–действие) отношения объектов. Авторы данной статьи за основу модели представления экспертных знаний взяли продукционную модель, являющуюся наряду с фреймами одним из наиболее популярных средств представления знаний в искусственном интеллекте. Для повышения наглядности и прозрачности процесса моделирования продукционные правила строятся в виде графовых моделей особой топологии. Представление продукционных правил с помощью графовых моделей Для построения моделей, сохраняющих интуитивную наглядность представления систем, авторами разработано программное средство G-IPS Ultimate (Graph Imitation Process System) имитационного моделирования в дискретном времени [3], позволяющее строить модели на основе графов специального вида. В данных моделях расширена область определения условий, которые позволяют учитывать исключительные ситуации в поведении системы на уровне модели. То есть областью определения переменных, обозначающих условия, является Ω={T, F, E}, где Т – «истина», F – «ложь», E – «ошибка». Система продукционных правил RGS в G-IPS Ultimate задается набором решающих графов RGt (рис. 1). RGt = – t-дольный конечный решающий граф (t≥3), где доли имеют следующий смысл. · · M=(q(t-1)1, q(t-1)2, …, q(t-1)z) – непустой вектор датчиков высшего порядка, z≥1. Датчик q(t-1)j отличается от датчиков более низкого порядка отсутствием логических связей, он определяется лишь собственным значением q(t-1)j=valÎΩ. · А={a1, a2, …, av} – непустое множество действий (правая доля решающего графа на рис. 1), v≥1; ai – идентификатор действия (вершина правой доли на рис. 1). · Следует отметить, что на каждое действие накладываются такие атрибуты, как приоритет (среди множества действий, подлежащих выполнению) и интервал вероятности, позволяющий задавать вероятности и корреляции выполнения действий. Программное средство G-IPS Ultimate Программное средство G-IPS Ultimate является развитием комплекса программ G-IPS [2], созданного в МЭИ в 2007–2008 гг., и предназначено для построения моделей процессов в виде решающих графов с последующей имитацией (рис. 2). Разработка велась в среде CodeGear Rad Studio 2007 с использованием дополнительных библиотек. Число строк авторского исходного кода составляет не менее 7 500, объем более 210 КБ, размер скомпилированного приложения 1,4 МБ.
Отличительными особенностями G-IPS Ultimate являются следующие. Программное средство представляет собой Windows-приложение с развитым пользовательским интерфейсом, в котором реализован универсальный механизм интерпретации решающих графов. Функциональность и интерфейс программы обеспечивают все необходимые режимы работы: разработка (создание моделей), эксперимент (автоматический и интерактивный прогоны моделей), анализ (просмотр журнала событий, анализ результатов экспериментов и кларификация – прояснения внутренней логики функционирования моделей). В G-IPS Ultimate реализован механизм взаимодействия модели с внешней средой. Среда задается подключаемыми модулями, которые представлены динамически компонуемыми библиотеками (DLL), благодаря чему у разработчиков модулей нет привязки к среде разработки. Предусмотрен также механизм воздействия пользователя на процесс имитации. История имитации процесса может сохраняться в журнале совершенных событий и состояний системы, что позволяет не только ускорить процесс отладки, но и пошагово изучить исследуемый процесс. Кроме того, история протекания процесса может записываться в виде, позволяющем последующий (например демонстрационный) повтор всех происходивших событий, включая воздействие внешней среды. В программном средстве реализован механизм проверки корректности структуры модели. Средствами G-IPS Ultimate возможно параллельное выполнение опроса датчиков, действий, интерпретации моделей. Программный комплекс позволяет описывать отдельные компоненты моделируемой системы на разном уровне абстракции. В нем реализован механизм тестового прогона моделей без подключения внешнего модуля, позволяющий быстро обнаружить ошибку проектирования на стадии создания модели. Комплекс G-IPS Ultimate может быть применен для решения широкого круга прикладных и учебных задач [4]. К основным направлениям развития данного комплекса следует отнести расширение набора инструментов анализа проводимых экспериментов средствами сбора различных статистических данных, а также реализацию механизма подключения других типов модулей (плагинов), таких как генераторы моделей, валидаторы и т.п. Литература 1. Ross, Sheldon M. Simulation. Academic Press, 4 ed., 2006. 312 p. 2. Карпухин И.Н., Незнанов А.А. Программные средства имитационного моделирования процессов принятия решений реального времени // Интегрированные модели, мягкие вычисления, вероятностные системы и комплексы программ в искусственном интеллекте. М.: Физматлит, 2009. Т. 2. С. 132–140. 3. Banks J., Carson J., Nelson B., Nicol D. Discrete-Event System Simulation. Prentice Hall, 3 ed., 2000. 600 p. 4. Карпухин И.Н., Незнанов А.А. Системы имитационного моделирования учебного назначения в российской высшей школе // Современные проблемы информационной безопасности и программной инженерии. М.: Спутник, 2011. C. 132–142. |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3137 |
Версия для печати Выпуск в формате PDF (5.19Мб) Скачать обложку в формате PDF (1.31Мб) |
| Статья опубликована в выпуске журнала № 2 за 2012 год. [ на стр. 156 ] |
Возможно, Вас заинтересуют следующие статьи схожих тематик:
- Применение информационных технологий при многоуровневой подготовке специалистов химико-технологического профиля
- Агентный подход при моделировании лесопожарных ситуаций
- Имитационное моделирование пневмогидромеханической системы в компьютерном тренажере
- Программный комплекс оценки факторов определения качества информации дистанционного зондирования Земли
- Некоторые результаты имитационного моделирования мультисервисных бортовых цифровых платформ стандарта DVB-RCS
Назад, к списку статей



 D=(X1, …, Xk) – вектор (k=t–2), в котором Xi=(qi1, qi2, …, qin) – непустой вектор датчиков i-го порядка, i≥1, n≥1 – конечные; X1 – вектор простых датчиков (или датчиков первого порядка), значения которых задает функция интерпретации, запрашивая исходный вектор извне; (X2, X3, …, Xk) – векторы (слои) датчиков более высокого порядка (второго, третьего и т.д.), их значения определяет функция интерпретации по значениям датчиков предыдущего порядка. Датчик qij задается парой , где valÎΩ – собственное значение датчика; Con={} – непустое множество пар , где idÎ[1..|Xi+1|] для слоев от 1 до (t–2) и idÎ[1..|M|] для датчиков (t–1)-го слоя – дуга, связывающая датчик qij с датчиком более высокого порядка, wÎΩ – вес дуги. То есть датчик определяется собственным значением val и взвешенными связями с датчиками более высокого порядка Con – множество пар «связь–вес», где вес дуги означает ожидаемое значение и визуализируется цветом (на рис. 1 – тонированием).
D=(X1, …, Xk) – вектор (k=t–2), в котором Xi=(qi1, qi2, …, qin) – непустой вектор датчиков i-го порядка, i≥1, n≥1 – конечные; X1 – вектор простых датчиков (или датчиков первого порядка), значения которых задает функция интерпретации, запрашивая исходный вектор извне; (X2, X3, …, Xk) – векторы (слои) датчиков более высокого порядка (второго, третьего и т.д.), их значения определяет функция интерпретации по значениям датчиков предыдущего порядка. Датчик qij задается парой , где valÎΩ – собственное значение датчика; Con={} – непустое множество пар , где idÎ[1..|Xi+1|] для слоев от 1 до (t–2) и idÎ[1..|M|] для датчиков (t–1)-го слоя – дуга, связывающая датчик qij с датчиком более высокого порядка, wÎΩ – вес дуги. То есть датчик определяется собственным значением val и взвешенными связями с датчиками более высокого порядка Con – множество пар «связь–вес», где вес дуги означает ожидаемое значение и визуализируется цветом (на рис. 1 – тонированием).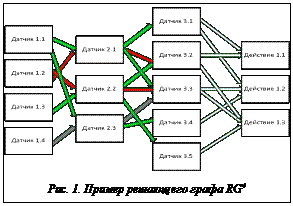 S – матрица размером |M|´|A|, устанавливающая связь между логическими правилами и действиями (незатонированные дуги решающего графа на рис. 1). Элементом данной матрицы является либо пустой элемент (отсутствие связи), либо тройка sij=, где ord – целое число, такое, что нуль означает отсутствие действия для данного датчика из М, а любое другое число – приоритет действия в наборе действий, подлежащих выполнению; lv – левая допустимая граница вероятности (из отрезка [1, 100]); rv – правая допустимая граница вероятности (из отрезка [1, 100]).
S – матрица размером |M|´|A|, устанавливающая связь между логическими правилами и действиями (незатонированные дуги решающего графа на рис. 1). Элементом данной матрицы является либо пустой элемент (отсутствие связи), либо тройка sij=, где ord – целое число, такое, что нуль означает отсутствие действия для данного датчика из М, а любое другое число – приоритет действия в наборе действий, подлежащих выполнению; lv – левая допустимая граница вероятности (из отрезка [1, 100]); rv – правая допустимая граница вероятности (из отрезка [1, 100]).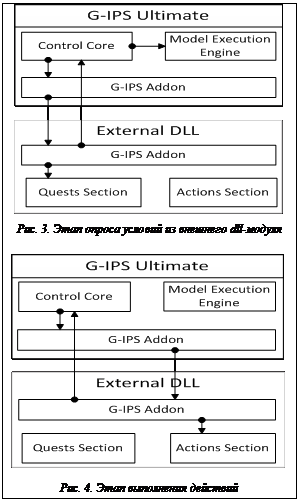 G-IPS Ultimate обеспечивает взаимодействие этой модели с внешним модулем (DLL). В процессе имитации каждый шаг прогона модели можно условно разделить на два этапа. На первом (рис. 3) система запрашивает значения элементарных датчиков из подключаемого внешнего модуля (DLL), используя низкоуровневый интерфейс G-IPS Addon. Помимо самого значения функции, из dll-модуля может поступить команда редактору G-IPS Ultimate через функцию обратного вызова, с помощью которой реализован ряд команд, таких как «добавить запись в текстовый журнал событий», «приостановить выполнение», «сохранить какую-либо величину в памяти» и др. После получения показателей простых датчиков система вычисляет значения остальных датчиков и составляет список действий, подлежащих выполнению. Затем наступает второй этап прогона модели – выполнение предписанных действий (рис. 4).
G-IPS Ultimate обеспечивает взаимодействие этой модели с внешним модулем (DLL). В процессе имитации каждый шаг прогона модели можно условно разделить на два этапа. На первом (рис. 3) система запрашивает значения элементарных датчиков из подключаемого внешнего модуля (DLL), используя низкоуровневый интерфейс G-IPS Addon. Помимо самого значения функции, из dll-модуля может поступить команда редактору G-IPS Ultimate через функцию обратного вызова, с помощью которой реализован ряд команд, таких как «добавить запись в текстовый журнал событий», «приостановить выполнение», «сохранить какую-либо величину в памяти» и др. После получения показателей простых датчиков система вычисляет значения остальных датчиков и составляет список действий, подлежащих выполнению. Затем наступает второй этап прогона модели – выполнение предписанных действий (рис. 4).