Программные продукты и системы

Большие объемы вычислений ограничивают применение высокоэффективных методов оптимизации в тех случаях, когда оптимальное решение должно быть получено за ограниченное время. Одним из направлений разрешения противоречия между увеличивающимися объемами вычислений и временными ограничениями может стать применение аппарата теории нейронных сетей, который находит все более широкое применение для решения инженерных задач (Галушкин А.И. Теория нейронных сетей. М., 2000).

С одной стороны, нейронным сетям свойственна высокая распараллеленность как для формализуемых, так и для неформализуемых задач. С другой стороны, нейронные сети претендуют на глобальность в смысле области приложения.

Выбор функционала оптимизации АР

Допустим, что требуется сформировать двухлучевую диаграмму направленности с максимальным средним коэффициентом направленного действия (КНД). В традиционной постановке подобная задача формулируется в следующем виде:

,                  (1)

,           (2)

где  – N-мерный вектор неизвестных комплекс­ных амплитуд токов, определяющий амплитудно-фазовое распределение в элементах АР; ;  – КНД N-элементной АР в направлении  и  соответственно.

Функционал вида (2) приводится к отношению эрмитовых форм, а для определения вектора оптимальных токов используется известная теорема об экстремальных свойствах характеристических чисел пучка эрмитовых форм. Одним из недостатков известного способа оптимизации является большой объем вычислений, требуемых для определения оптимального решения. Более существенный недостаток известного способа в том, что при использовании функционала (2) в результате оптимизации значения  и  существенно отличаются, что неприемлемо в практических задачах (Мануилов Б.Д., Башлы П.Н., Безуглов Ю.Д., Кузнецов А.А. Формирование многолепестковых диаграмм направленности антенных решеток со стабилизацией положения и уровней лучей. //Сб. докл. междунар. конф. «Излучение и рассеяние радиоволн», Таганрог, 2005).

В связи с этим предлагается использовать более сложный функционал:

,                       (3)

причем постановка задачи оптимизации (1) за исключением вида функционала не меняется.

Сложность решения задачи оптимизации АР с функционалом (3) заключается в невозможности применения теоремы об экстремальных свойствах характеристических чисел пучка эрмитовых форм, позволяющей аналитически определить вектор оптимальных комплексных токов. Выполнив преобразования функционала (3), с учетом представления КНД в виде отношения эрмитовых форм получим:

,            (4)

где ,  и  – эрмитовы матрицы порядка N;  – символ Кронекерова произведения матриц. Таким образом, функционал (3) сводится к отношению эрмитовых форм (4), порядок которых N2. Очевидно, что в данном случае теорема об экстремальных свойствах характеристических чисел пучка эрмитовых форм не может быть использована, поскольку порядок вектора – , максимизирующего функционал (4) – , тогда как в составе АР N управляемых каналов.

Синтез нейронной сети

Поскольку максимизируемый функционал (4) в рассматриваемой задаче имеет физический смысл только как функция N переменных, для синтеза нейронной сети воспользуемся градиентным методом.

Для этого определим градиент функционала (4), для которого в общем случае будем полагать матрицы , входящие в знаменатель, различными:

(5)

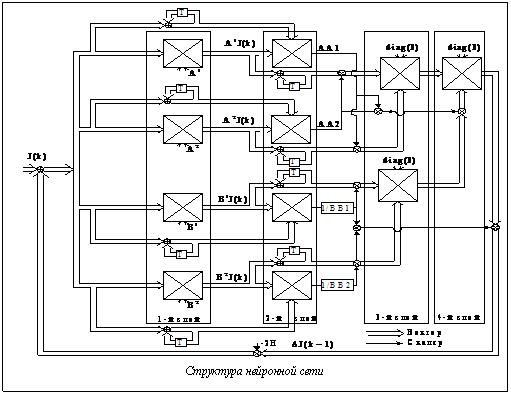
Синтез структуры нейронной сети для решения задачи оптимизации основан на свойстве градиента функционала (4), обращающегося в ноль в точках экстремума. Исходя из этого, положим в качестве входного сигнала нейронной сети вектор J, а в качестве выходного – градиент функционала (5) DJ. Структура нейронной сети будет определяться выражением (5), как показано на рисунке. Из анализа выражения (5) и рисунка можно сделать вывод о высокой степени распараллеленности операции вычисления градиента функционала в нейросетевых архитектурах, что достаточно важно с учетом итерационного характера градиентных методов поиска экстремума.

Алгоритм функционирования нейронной сети на k-м шаге записывается в следующем виде:

,                        (6)

где H – параметр, определяющий скорость настройки сети.

Условием определения оптимального вектора токов  будем считать равенство или стремление к нулю вектора DJ.

Результаты численного эксперимента

Для численного эксперимента была использована модель 25-элементной АР ненаправленных излучателей. На первом этапе сравнивалась эффективность известного и предлагаемого метода  оптимизации.

Для этого проводились два численных эксперимента. Результаты первого приведены в таблице 1, где показана зависимость распределенного КНД решетки  от углового положения лучей при заданном направлении одного из лучей по нормали  . Второй эксперимент был направлен на выявление зависимости КНД решетки от углового положения максимумов лучей, каждый из которых отклонен от нормали. Результаты приводятся в таблице 2.

Таблица 1

Зависимость  от направлений лучей  и

Таблица 2

Зависимость  от направлений лучей  и

Анализ таблиц 1 и 2 позволяет сделать следующие выводы:

-    оптимизация АР с функционалом (3) обеспечивает более высокое значение распределенного КНД, при этом энергия АР между лучами распределяется более равномерно;

-    неравномерность распределения энергии между формируемыми лучами при оптимизации известными методами более выражена при отклонении обоих лучей от нормали;

-    число итераций, требуемых для получения оптимального решения предлагаемым методом, существенно зависит от заданных направлений формируемых лучей, что особенно заметно для двух лучей, максимально отклоненных от нормали.

Второй этап исследований заключается в анализе возможности сокращения числа итераций при определении оптимального решения предлагаемым методом.

Как известно, градиентный метод, положенный в основу работы нейронной сети, основывается на последовательном приближении к экстремуму заданного критерия путем вычисления его градиента в каждой точке. Для ускорения процесса настройки нейронной сети можно использовать параметр Н, получивший название шаг настройки сети.

В таблице 3 приводятся результаты исследований, показывающие зависимость числа итераций при определении оптимального вектора токов для случая  и .

Таблица 3

Зависимость числа итераций Р от параметра Н

Выполненные исследования выявили существенную зависимость числа итераций Р, требуемых для определения оптимального решения, от параметра Н. При этом сокращение числа итераций на два порядка практически не влияет на значение распределенного КНД (табл. 3). Такой результат обусловлен особенностями максимизируемого критерия, который в рассматриваемой задаче имеет единственный глобальный экстремум.

Таким образом, в работе решена комплексная задача анализа возможностей нового метода оптимизации АР и проведено его сравнение с известными методами. Полученные результаты позволяют обосновать возможность использования нейроподобных сетей для снятия противоречия между возрастающими объемами вычислений и ограничением на время, требуемое для настройки АР в режим, оптимальный по заданному критерию.