Многофункциональный имитатор нейронных сетей
| Солдатова О.П. (op-soldatova@yandex.ru) - (Самарский государственный аэрокосмический университет им. академика С.П. Королева (национальный исследовательский университет), кандидат технических наук | |
| Ключевые слова: прогнозирование., классификация, алгоритмы обучения, нейроимитатор, системы нечеткого вывода, нейронные сети |
|
| Keywords: , classification, learning algorithms, neural simulator, fuzzy logic, , neural network |
|
|
|
|
Для решения конкретных задач с помощью нейронных сетей необходимы модель нейронных сетей, а также определенный инструментарий. Можно выделить два крупных класса програм- мных моделей нейронных сетей: специализированное ПО, нацеленное на решение конкретного и, как правило, достаточно узкого круга задач с помощью одной модели нейронной сети со специально подобранной топологией, и универсальные программы-нейроимитаторы, включающие в себя различные топологии нейронных сетей и предоставляющие возможность настройки каждой из поддерживаемых топологий, что позволяет конструировать нейронные сети для решения различных классов задач. В данной статье представлен нейроимитатор «Нейрокомбайн», в котором поддерживаются модели нейронных сетей: многослойный персептрон, нечеткий многослойный персептрон, радиально-базисные сети и гипер-радиально-базисные сети, сеть Ванга–Менделя, сеть Такаги–Сугэно–Канга (TSK), сеть, реализующая модель Мамдани–Заде и сеть, реализующая модель Цукамото. «Нейрокомбайн» выполняет следующие функции: – создание нейронной сети определенного типа с указанием параметров для начальной инициализации данной сети; – загрузка и необходимая предобработка обучающих и тестовых данных из текстовых файлов и файлов в формате Microsoft Office Excel; – графическое отображение структуры нейронных сетей; – обучение нейронной сети с детальной настройкой процесса обучения, визуализацией хода обучения и предоставлением данных о качестве обучения; – тестирование нейронной сети на тестовой выборке с визуализацией результатов тестирования; – сохранение нейронных сетей в файл и загрузка из файла. Для классических топологий нейронных сетей, таких как многослойный персептрон и радиально-базисные сети, реализованы следующие алгоритмы обучения: алгоритм наискорейшего спуска, метод обратного распространения ошибки, гибридный алгоритм для обучения радиально-базисных сетей, а также алгоритм К-усреднений и алгоритм построения деревьев классификации для инициализации центров радиально-базисных функций. Особое внимание в «Нейрокомбайне» уделено моделям нечетких нейронных сетей. В случае линейной неразделимости классов и неустойчивого поведения алгоритма обучения имеет смысл использовать гибридную сеть, включающую в себя слой с нечеткой самоорганизацией и многослойный персептрон. Функции активации нейронов нечеткого слоя такой сети являются радиально- базисными (в виде функции Гаусса). Выходы нейронов нечеткого слоя используются в качестве входов традиционного многослойного персепт- рона. Наблюдается усиление интереса к гибридным моделям нейронных сетей и систем нечеткого вывода, основанных на продукционных правилах «если – то» следующего вида: если x это A, то y это B, (1) где A и B – нечеткие множества, идентифицированные через соответствующие функции принадлежности для переменных x и y. Это обобщенное (нечеткое) правило modus ponens. Нечеткое рассуждение – процедура, позволяющая определить заключение, вытекающее из множества правил «если – то»: если x1 это A1 и x2 это A2 и … и xN это AN, то y это B. (2) Переменные x1, x2, …, xN образуют N-мерный входной вектор x, составляющий аргумент условия, в котором A1, A2, …, AN и B обозначают величины соответствующего коэффициента принадлежности mA(x) и mB(y). Случайное значение функции принадлежности mA(x), где x – вектор x=x1, x2, …, xN, относящееся к условию импликации, должно интерпретироваться с использованием нечетких операций. Представленное формулой (2) продукционное правило вывода является основой базы знаний в системе нечеткого вывода Мамдани–Заде. Как правило, в модели Мамдани–Заде присутствуют [1]: – оператор логического или алгебраического произведения для агрегации всех компонентов вектора x условия; – оператор логического или алгебраического произведения для определения значения функции принадлежности для всей импликации A®B; – оператор логической суммы для агрегации равнозначных результатов импликации многих правил; – оператор дефуззификации, трансформирующий нечеткий результат m(y) в четкое значение переменной y. В модели нечеткого вывода TSK заключение определяется функциональной зависимостью. Благодаря этому дефуззификатор на выходе системы не требуется, а сама модель вывода значительно упрощается [1]. Общая форма модели TSK: если x1 это A1 и x2 это A2 и … и xN это AN, то y=f(x1, x2, …, xN), (3) где f(x1, x2, …, xN) – четкая функция. Условие модели TSK аналогично модели Мамдани–Заде, принципиальное отличие касается заключения, которое чаще всего представляется в виде полиномиальной функции нескольких переменных. Классическое представление этой функции – полином первого порядка:
в котором коэффициенты p0, p1, …, pN являются весами, подбираемыми в процессе обучения. Если в модели TSK используется M правил вывода, выход системы определяется как среднее нормализованное взвешенное значение. Если каждому правилу приписать вес wi (интерпретируются как
Веса wi являются нелинейными параметрами функции y, уточняемыми в процессе обучения. В модели Цукамото в качестве функций заключения используются монотонные (возрастающие или убывающие) функции f –1 [2]. Заключения правил формируются путем обратного преобразования этих функций по полученным значениям предпосылок данных правил: если x1 это A1 и x2 это A2 и … и xN это AN, то y= f –1(w), (6) где w – уровень срабатывания предпосылки правила. Условие модели Цукамото аналогично модели Мамдани–Заде, принципиальное отличие касается заключения. Если в модели Цукамото используется M правил вывода, выход системы определяется как среднее взвешенное значение. Если приписать каждому правилу вес wi (интерпретируется как
где yi=fi–1(wi) – значение аргумента функции fi, при котором wi=fi(yi) [2]. В «Нейрокомбайне» использована модель нечеткой продукционной сети Ванга–Менделя в классической топологии с одним выходом, а также разработана ее модификация с несколькими выходами. Для данной сети создана и реализована модификация алгоритма наискорейшего спуска и метода обратного распространения ошибки. Для сети Ванга–Менделя также реализованы гибридный алгоритм обучения, алгоритмы инициализации параметров функции фуззификации C-Means и алгоритм разностного группирования [1]. Поскольку для модели вывода Мамдани–Заде не существует каноническая структура нейронной сети, в нейроимитаторе предлагается одна из ее возможных реализаций (рис. 1). В «Нейрокомбайне» реализована сеть TSK в классической топологии с одним выходом и создана модификация модели с несколькими выхо Структура нечеткой сети на основе модели вывода Цукамото подразумевает использование функции принадлежности сигмоидального типа в качестве функции фуззификации для входных переменных и для заключений правил. В «Нейрокомбайне» разработана и реализована модель нечеткой нейронной сети на основе модели Цукамото с несколькими выходами (рис. 2). Для данной сети разработана и реализована модификация алгоритма наискорейшего спуска и метода обратного распространения ошибки. Для сети на основе модели Цукамото также реализованы гибридный алгоритм обучения, алгоритмы инициализации параметров функции фуззификации C-Means и алгоритм разностного группирования.
Суммарное СКО погрешности определяется формулой
Формула для средней приведенной погрешности такова:
где djmax=maxtdj,t, djmin=mint dj,t. При решении задачи классификации входные элементы сети используются как приемники классификационных признаков. Таким образом, число входов сети однозначно определяется числом характеристик объекта классификации в решаемой задаче. Для исследования эффективности решения задачи классификации была выбрана стандартная задача классификации вин. Набор данных представляет собой результаты химического анализа вин из винограда, выращенного в одном регионе, но принадлежащего к трем различным сортам. В ходе анализа выделено процентное содержание 13 составляющих вин, присутствующих в каждом из трех сортов. Задача – определить принадлежность вина с заданными характеристиками к одному из трех сортов. Общий объем данных – 178 образцов. Из них на 142 образцах проводилось обучение, а оставшиеся 36 использовались для тестирования. Результаты исследования эффективности решения задачи классификации нечеткими нейронными сетями приведены в таблице 1, где K определяет число классов, N – число правил вывода в БЗ. Таблица 1 Результаты исследования решения задачи классификации
Как видно из результатов исследования эффективности решения задачи классификации, наилучшие результаты показали сети Ванга–Менделя и TSK. Для прогноза был выбран объем валового внутреннего продукта России на период с 1999 по 2009 годы, всего 43 значения. Обучение проводилось по первым 33 числам, а тестирование – по последним 10. Нейронные сети имеют 4 входа. Результаты исследования эффективности решения задачи прогнозирования нечеткими нейронными сетями приведены в таблице 2. Таблица 2 Результаты исследования решения задачи прогноза
Примечание: K – дальность прогноза (число выходов сети), N – число правил вывода в БЗ. Как видно из результатов исследования эффективности решения задачи прогнозирования, наилучшие результаты показали сети, реализующие модели Мамдани–Заде и Цукамото. Таким образом, приведенные результаты исследований показывают актуальность и применимость нечетких нейронных сетей при решении широко встречающихся задач классификации, прогнозирования и аппроксимации. Это подтверждает их статус универсального инструмента для обработки информации при решении различных задач. А известные алгоритмы обучения обеспечивают минимальную погрешность, значение которой колеблется в зависимости от выбранной модели. Литература 1. Осовский С. Нейронные сети для обработки информации; [пер. с польск. И.Д. Рудинского]. М.: Финансы и статистика, 2002. 344 с. 2. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы; [пер. с польск. И.Д. Рудинского]. М.: Горячая линия–Телеком, 2007. 452 с. 3. Борисов В.В., Круглов В.В., Федулов А.С. Нечеткие модели и сети. М.: Горячая линия–Телеком, 2007. 284 с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
http://swsys.ru/index.php?page=article&id=3207&lang=%E2%8C%A9=en |
|
Perhaps, you might be interested in the following articles of similar topics:
- Нейросетевой метод обнаружения вредоносных программ на платформе Android
- Разработка базы данных и конвертера для извлечения и анализа специализированных данных, получаемых с медицинского аппарата
- Трехступенчатый эволюционный метод формирования коллективов нейронных сетей для решения задач классификации
- Моделирование взаимодействия агентов в многоагентной системе с помощью цветных сетей Петри и нечеткой логики
- Комплекс программного обеспечения для оптимизации надежности однородных нейронных структур

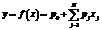 , (4)
, (4)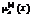 в форме алгебраического произведения), выходной сигнал можно представить в виде
в форме алгебраического произведения), выходной сигнал можно представить в виде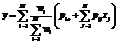 . (5)
. (5)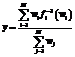 , (7)
, (7)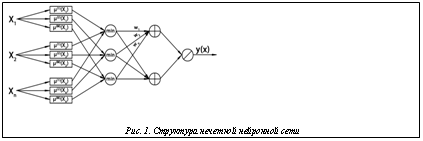 дами. Для данной сети разработана и реализована модификация алгоритма наискорейшего спуска и метода обратного распространения ошибки. Для сети TSK также реализованы гибридный алгоритм обучения, алгоритмы инициализации центров функции фуззификации C-Means и алгоритм разностного группирования.
дами. Для данной сети разработана и реализована модификация алгоритма наискорейшего спуска и метода обратного распространения ошибки. Для сети TSK также реализованы гибридный алгоритм обучения, алгоритмы инициализации центров функции фуззификации C-Means и алгоритм разностного группирования.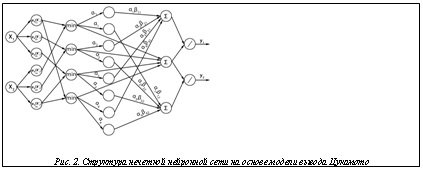 Эффективность предложенных моделей нейронных сетей исследовалась на примере решения задач классификации и прогнозирования. Показателем качества обучения и тестирования сети обычно является значение разности между фактическими yj,t и эталонными dj,t выходными значениями для всех M выходов (j=1, 2, …, M) сетей и всех p пар фактических и эталонных векторов t=1, 2, …, p. Для количественной оценки этой разности были рассчитаны суммарное среднеквадратическое отклонение (СКО) погрешности обучения и средняя приведенная погрешность.
Эффективность предложенных моделей нейронных сетей исследовалась на примере решения задач классификации и прогнозирования. Показателем качества обучения и тестирования сети обычно является значение разности между фактическими yj,t и эталонными dj,t выходными значениями для всех M выходов (j=1, 2, …, M) сетей и всех p пар фактических и эталонных векторов t=1, 2, …, p. Для количественной оценки этой разности были рассчитаны суммарное среднеквадратическое отклонение (СКО) погрешности обучения и средняя приведенная погрешность.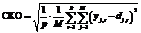 . (8)
. (8)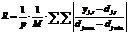 , (9)
, (9)