Автоматизация управления жизненным циклом продукции на производственном предприятии связана с применением современных принципов управления сложными организационно-техническими системами [1], одним из которых является обеспечение информационного взаимодействия персонала предприятия в едином информационном пространстве. Этот аспект касается задачи производственного планирования [2] и выражается в новой возможности постоянного перестроения оперативного плана под воздействием внешних событий. В такой ситуации от разработчиков ПО требуются новые подходы к проектированию и реализации автоматизированных систем планирования.
Например, применение этих технологий в мелкосерийном, опытном и наукоемком производстве вызывает определенные трудности. Детальное планирование возможно в случае, когда известны технологические процессы, а точность планирования серьезно зависит от адекватности нормирования работы разной квалификации. В случаях, когда для изготовления изделия можно использовать различные технологии, технологические процессы требуют согласования с мастерами высокой квалификации, а при нормировании необходимо учитывать значительную неопределенность, возникает новая актуальная задача согласованного взаимодействия экономиста и технолога как на этапе планирования, так и на этапе выполнения плана.
Классическая постановка задачи планирования, заключающаяся в определении целевых функций и ограничений, не позволяет решить ее, так как нацелена на оптимизацию всего расписания в целом, без учета возможных изменений. Применение аналогий с живыми системами [3], например мультиагентных технологий, не может обеспечить требуемую предсказуемость и управляемость, что приводит к сложности интерпретации результатов планирования и трудностям применения на практике. Решить данную проблему можно, используя гибридный подход, основанный на построении на базе распределенной (например мультиагентной) архитектуры системы информационного управления взаимодействием персонала предприятия, дополняющей классические подсистемы сетевой оптимизации. Такая система управления будет задавать условия, протоколы и регламенты, в соответствии с которыми пользователи интегрированной информационной среды обмениваются информацией в процессе выработки и согласования решений. При этом их необходимо сформировать таким образом, чтобы обеспечить требуемые показатели эффективности деятельности предприятия.
Отметим, что эти условия взаимодействия будут меняться во времени, что позволяет ситуационно управлять обработкой событий различного характера.
Для задач производственного планирования в качестве целей, определяющих применение этих условий, целесообразно выбрать дилемму поиска баланса между оптимальной производительностью, операционными расходами и межоперационными запасами [4]. Обеспечить конструктивное решение этой дилеммы можно путем формирования частных противоречий между участниками жизненного цикла продукции, выражающихся в конкуренции за ресурсы, задания или время их выполнения. Технически реализовать такое взаимодействие можно путем введения ограничений или расширений информации, попадающей различным пользователям интегрированной информационной среды в разные моменты времени, обеспечивая таким образом требуемую ритмичность процессов информационного взаимодействия персонала предприятия [5, 6].
Рассмотрим задачу внутрицехового планирования на период времени T множества заказов О={o1, o2, …, on}, где каждый заказ oi=(ti0, pi, ci0) описывается следующими значениями: ti0 – максимальная трудоемкость производства (длительность выполнения заказа в нормо-часах); pi – стоимость выполненного цехом заказа; ci0 – максимальная стоимость выполнения заказа.
В зависимости от выбранной технологии выполнения заказа S(oi)={s1(oi), s2(oi), …, sm(oi)} возможно сокращение длительности и стоимости его выполнения на определенную величину: Δtij – сокращение длительности производства для заказа i при использовании технологии j; Δcij – сокращение стоимости выполнения заказа i при использовании технологии j.
Рассмотрим случай, когда суммарная трудоемкость выполнения выбранного набора заказов заведомо превышает производственные возможности цеха в рамках планируемого периода. Получаем матрицу D размера N´M, элементами которой являются пары значений:
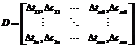 .
.
Пересчитаем результирующие значения длительности и стоимости производства для i-го заказа при использовании j-й технологии: tij=ti0–Δtij; cij=ci0–Δcij.
В свою очередь, прибыль от выполнения i-го заказа при использовании j-й технологии будет: Δpij=pi–cij=pi–(ci0–Δcij). Составим результирующую матрицу G, содержащую значения прибыли заказов и длительности их производства с использованием имеющихся технологий:
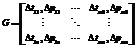 .
.
Таким образом, сформулируем цель максимизации прибыли, которую может обеспечить выбор используемых технологий производства заказов из заданного множества О. В игровой постановке данную задачу представим следующим образом. Экономист заинтересован в том, чтобы максимизировать прибыль от выполнения каждого заказа, а цель технолога – максимально сократить срок выполнения каждого заказа. Экономист может выбирать заказы из некоего портфеля, в то время как технолог определяет технологии их выполнения. Предположим, что экономист и технолог выбирают заказ и технологию по очереди, в таком случае получается бескоалиционная неантагонистическая игра с полной информацией.
В данной задаче возможно возникновение нескольких ситуаций, оптимальных по Парето, и можно заключить, что в рассматриваемой игре имеет место гонка за право первого хода. Поэтому имеет смысл рассмотреть решение задачи с двух сторон: с правом первого хода и технолога, и экономиста. Важно отметить, что при этом возникает парадокс, поскольку игра с правом первого хода технолога заведомо более выигрышна с экономической точки зрения, а игра с правом первого хода экономиста заведомо более выигрышна с технологической точки зрения. Данный парадокс обусловлен тем, что игрок, получающий право первого хода, точно знает, каким образом отреагирует его оппонент (игра с полной информацией), поэтому из всех своих вариантов ему придется выбрать тот, который обеспечит ему максимальный выигрыш с учетом действий оппонента.
Необходимо определить, приведет ли такое взаимодействие, реализованное в имитационной модели, к повышению эффективности по сравнению с обычными стратегиями оптимизации. Для этого была разработана имитационная модель и проведен ряд экспериментов для разных вариантов прибыльности заказов. При определении прибыльности было сделано предположение о том, что стоимость заказа зависит от его сложности, а сложность заказа напрямую определяет его трудоемкость.
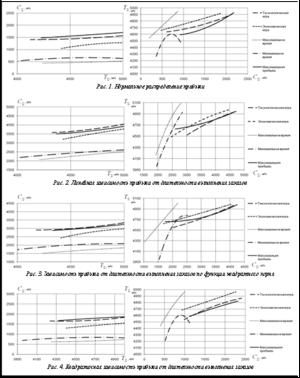 На рисунках 1–4 приведены графики трендов, аппроксимирующих зависимость суммарной прибыли от выполнения заказов СS от суммарной длительности выполнения заказов TS (слева) и зависимость суммарной длительности выполнения заказов TS от суммарной прибыли от выполнения заказов СS (справа). Результат каждого эксперимента представляет собой пару значений: суммарные технологические затраты выбранных заказов и их суммарная прибыль. Все тренды, показанные на графиках, построены посредством полиномиальной аппроксимации второй степени.
На рисунках 1–4 приведены графики трендов, аппроксимирующих зависимость суммарной прибыли от выполнения заказов СS от суммарной длительности выполнения заказов TS (слева) и зависимость суммарной длительности выполнения заказов TS от суммарной прибыли от выполнения заказов СS (справа). Результат каждого эксперимента представляет собой пару значений: суммарные технологические затраты выбранных заказов и их суммарная прибыль. Все тренды, показанные на графиках, построены посредством полиномиальной аппроксимации второй степени.
Как видно на рисунке 1, в случае нормального распределения стоимости заказов игровой подход (вне зависимости от права первого хода) уступает по экономической эффективности выбору заказов по максимальной прибыли. Принципы выборки заказов по максимальной/минимальной длительности выполнения значительно уступают остальным способам выборки. При нормальном распределении стоимости заказов наибольшей технологической привлекательностью обладает игра с правом первого хода экономиста. На рисунке 2 показано, что, если стоимость заказов линейно зависит от длительности их выполнения, игровой подход с правом первого хода технолога имеет некоторое преимущество перед всеми остальными способами выборки заказов. Принципы выборки заказов по максимальной/минимальной длительности выполнения значительно уступают остальным способам выборки. При линейной зависи- мости стоимости заказов от длительности наибольшей технологической привлекательностью обладает игра с правом первого хода экономиста.
На рисунке 3 видно, что, если стоимость заказов зависит от длительности их выполнения по функции квадратного корня, игровой подход с правом первого хода технолога имеет незначительное экономическое преимущество перед выборкой заказов по максимальной прибыли. Можно предположить, что с увеличением количества заказов и временного интервала разница в экономической эффективности этих двух методов будет увеличиваться. Принципы выборки заказов по максимальной/минимальной длительности выполнения значительно уступают остальным способам выборки. Рисунок 4 показывает, что, если стоимость заказов квадратично зависит от длительности их выполнения, выбор заказов по их максимальной прибыли имеет преимущество по уровню экономической прибыли. Можно предположить, что с увеличением количества заказов и временного интервала экономическая эффективность технологической игры с правом первого хода будет расти быстрее, чем при выборке по максимальной прибыли. Принципы выборки заказов по максимальной/минимальной длительности выполнения значительно уступают остальным способам выборки.
Полученные результаты позволяют сделать вывод о том, что применение игровой модели принятия решений с правом первого хода технолога может быть экономически оправданным, если между прибылью и длительностью исполнения заказов существует линейная зависимость или зависимость по функции квадратного корня. Если же прибыль от выполнения заказов подчиняется нормальному распределению или квадратичной зависимости, классическая выборка заказов с максимальной прибылью оказывается экономически более выгодной. Другие способы выборки, рассматриваемые в рамках данной статьи, всегда уступают по экономической эффективности. С технологической точки зрения во всех экспериментах наиболее выгодной оказалась выборка заказов по игре с правом первого хода экономиста.
Литература
1. Бурков В.Н., Коргин Н.А., Новиков Д.А. Введение в теорию управления организационными системами. М.: Либроком, 2009. 264 с.
2. Иващенко А.В., Андреев М.В. Автоматизированная система адаптивного управления производственным планом // Автоматизация и современные технологии. 2009. № 2. С. 37–41.
3. Leitão P., Barbosa J. Biological inspiration to solve complexity in intelligent and adaptive manufacturing systems // 10th IFAC Workshop on Intelligent Manufacturing Systems (IMS'10). July 1–2, 2010. Lisbon, Portugal, pp. 221–226.
4. Детмер У. Теория ограничений Голдратта. Системный подход к непрерывному совершенствованию; [пер. У. Саламатовой]. М.: Альбина Паблишер, 2010. 448 с.
5. Иващенко А.В. Модель многоакторной интегрированной информационной среды предприятия // Вестн. СамГУПС, 2012. № 1 (15). С. 103–109.
6. Иващенко А.В. Управление согласованным взаимодействием пользователей интегрированной информационной среды предприятия. Самара: СНЦ РАН, 2011. 100 с.



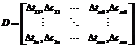 .
.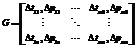 .
.
