Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Прогнозирование надежности программного обеспечения на основе модели неоднородного пуассоновского процесса и бутстреп-методов
Аннотация:Описывается новая математическая модель надежности ПО, построенная на основе математической модели не-однородного пуассоновского процесса. Основной идеей предлагаемого в статье метода прогнозирования является метод размножения выборок данных, содержащих два исходных набора: кумулятивное время исполнения программ и количество ошибок, зафиксированных за это время. В качестве метода размножения рандомизированных выборок взята бутстреп-технология, использующая формирование случайных величин, имеющих распределение Пуассона. Предложены алгоритмы нахождения оценок параметров и прогнозирования показателей надежности ПО. Первый алгоритм служит для оценки интенсивности ошибок, ожидаемых при последующих исполнениях программ. В алго-ритме используется датчик случайных чисел, на основе которого строятся рандомизированные выборки и формиру-ются массивы случайных чисел, распределенных по пуассоновскому закону. Второй алгоритм позволяет оценивать интенсивность обнаружения ошибок. Он использует данные выборок из первого алгоритма и действует по методу максимального правдоподобия. В статье описывается общая процедура прогнозирования ожидаемого количества ошибок, которые могут проявиться при последующем исполнении программ на некотором интервале времени, сле-дующем за кумулятивным интервалом наблюдения. Предложенный метод прогнозирования был реализован в виде программы, написанной на языке программирования Паскаль в свободной среде программирования PascalABC.NET. Кроме того, описаны примеры использования программы прогнозирования при некоторых тестовых данных.
Abstract:A new mathematical model of software reliability is described, based on mathematical model of inhomogeneous Poisson process. The basic idea of the proposed in the article forecasting method is a method of reproduction of data samplings, containing two original sets: the cumulative program execution time and number of errors committed during this time. As a method of a randomized sampling reproduction a bootstrap technology is taking which uses random quantities, having a Poisson distribution. Algorithms of parameter estimate and forecasting indicators of software reliability are suggested. The first algorithm is used to assess the intensity of errors expected in subsequent versions of the software. The algorithm uses a random number sensor on which basis randomized sampling and random arrays are arranged under Poisson law. The second algorithm makes it possible to evaluate the intensity of error detection. He uses data samples from the first algorithm and operates according to the method of maximum likelihood. The article describes the general procedure for forecasting the expected number of errors that can occur during a subsequent program run at a certain time interval, following a cumulative period of observation. The proposed forecasting method was realized in the form of a program written in Pascal programming language in the free programming environment PascalABC.NET. It also describes examples of using forecasting software with some test data.
| Авторы: Гуда А.Н. (guda@rgups.ru ) - Ростовский государственный университет путей сообщения (профессор, проректор), Ростов-на-Дону, Россия, доктор технических наук, Чубейко С.В. (greyc@mail.ru) - Ростовский государственный университет путей сообщения, Ростов-на-Дону, Россия, кандидат технических наук | |
| Ключевые слова: бутстреп-технология., неоднородный пуассоновский процесс, надежность по |
|
| Keywords: the non-homogenous Poisson process, the non-homogenous Poisson process, reliability of the software |
|
| Количество просмотров: 7145 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
За последнее десятилетие в области разработки ПО произошли коренные изменения. Средства разработки ПО позволяют автоматически генерировать исходный текст, использовать шаблоны проектирования программ, повторно использовать компоненты, объекты, выполнять рефакторинг, а также имеют другие возможности, ускоряющие проектирование ПО. В то же время все эти широкие возможности не только увеличивают количество программных подсистем в разрабатываемом проекте, но и усложняют взаимосвязи между ними, неизбежно усложняя процесс поиска ошибок в проекте и снижая его надежность. В связи с этим основным инструментарием обеспечения надежности программного проекта являются методы тестирования на разных стадиях жизненного цикла программ (особенно на завершающей) с целью обнаружения ошибок при некорректно предоставляемых данных и построение упрощенных формальных спецификаций сложного «большого» проекта, отражающих его основные свойства и требования на том или ином формально-логическом языке для логического обоснования корректности исходного программного проекта. Однако существует математическая теория надежности ПО, строящаяся подобно математической теории систем. Значительным плюсом такого подхода к надежности ПО является не только возможность констатации фактов вида «в ПО есть ошибки либо с такой-то вероятностью нет ошибок», но и более широкая постановка вопроса: как на основании имеющихся и измеряемых в процессе работы ПО показателей, не имея доступа к исходному тексту программ, математически обоснованно рассчитать вероятность появления или количество ошибок через какое-либо время работы программы в будущем. Одному из таких способов посвящена данная работа. Математическая модель Предлагаемая авторами модель будет опираться на математическую модель из работы [1], в основе которой лежит неоднородный пуассоновский процесс {N(t), t³0}, характеризующийся следующими допущениями. Во-первых, программы запускаются в неперекрывающиеся интервалы времени [(0, t1), (t1, t2), …, (ti–1, ti), …, (tm–1, tm)]. Во-вторых, количество ошибок (f1, f2, …, fm) на каждом интервале не зависит от других интервалов, а каждая ошибка устраняется сразу после ее выявления. В-третьих, кумулятивное количество ошибок, обнаруженных на момент времени t, имеет пуассоновское распределение со средним m(t). И наконец, каждая ошибка может быть обнаружена с одинаковой вероятностью, приводит к одинаковым негативным последствиям, интервалы обнаружения ошибок имеют одинаковую размерность (сутки, неделя, месяц и т.п.). Функция m(t) является неубывающей и ограниченной сверху, то есть m(t)=0 при t=0, m(t)=a при t®¥, (1) где a – количество ошибок в ПО, которое в принципе в нем содержится и может быть обнаружено. Если принять, что количество ошибок в ПО, обнаруженных на интервале времени Dt, пропорционально количеству ошибок, имеющихся в ПО, но пока не обнаруженных, то с учетом (1) имеем:
Из выражения (2) при Dt®0 получаем дифференциальное уравнение
решая которое с условиями (1), находим среднее количество ошибок
Интенсивность ошибок из выражений (3) и (4) получаем как
Процесс моделирования ошибок с функцией интенсивности l(t) выполняется в соответствии со стохастическим процессом: – если не возникают ошибки за время Dt, то
– если за время Dt возникает одна ошибка,
– если за время Dt возникают две (и более) ошибки, P{N(t, Dt)–N(t)=2}=o(Dt). (8) Таким образом, возникновение fi ошибок на интервале времени (0, ti) будет
где i – некий интервал времени, в процессе которого программа загружена и исполняется; fi – число ошибок, возникших за период времени i; ti – кумулятивное время исполнения программы, включая интервал i, то есть совокупность всех времен исполнения программы; m(ti) – функция средней интенсивности ошибок для времени, Для дальнейших численных расчетов среднюю интенсивность ошибок можно приравнять к среднему количеству ошибок li, обнаруживаемых на i-м интервале, и тогда выражение (9) будет представлять собой известную модель Гоэла–Окумото (см. [1]): Учитывая, что в данном случае рассматривается неоднородный пуассоновский процесс, а, следовательно, для каждого ti-го интервала времени функция интенсивности может изменяться, продолжим рассуждения следующим образом. Параметр li определяется по выражению (4) как
где m – интенсивность устранения ошибок. Задача моделирования состоит в определении параметров интенсивности обнаружения и устранения ошибок (l и m соответственно) в ПО в выражении (8), причем для каждого ti-го интервала времени. Очевидно, что в данном случае при наличии выборки данных, содержащей кумулятивное количество обнаруженных ошибок к некоторому ti-му интервалу времени, для определения параметров l и m подходящим оказывается метод максимального правдоподобия [2]. Функция правдоподобия имеет вид
где I – общее число временных интервалов наблюдения ошибок. Прологарифмируем выражение (11):
Подставив вместо li в выражении (12) функцию из выражения (10), получаем
Чтобы найти максимум для данной функции, возьмем частную производную по переменной l:
Просуммировав выражение (14), получаем
где f+ – кумулятивное число ошибок для всех i-х периодов времени. Приравнивая к нулю производную (14), получаем выражение для оценки интенсивности обнаружения ошибок
Подставив
Рассмотрим нахождение начального значения m. Пусть
Из выражений (16)–(18) видно, что s и x связаны соотношениями s=[x/(1–x)], x=[s/(1+s)]. Начальное значение x0 можно отыскать по формуле
то есть разделив количество ошибок, полученных за первую половину времени исполнения программы, на количество ошибок, полученных за вторую половину времени исполнения программы. Далее подставляем полученное значение x в формулу (17) и получаем начальное значение m, для уточнения которого используется итеративный процесс
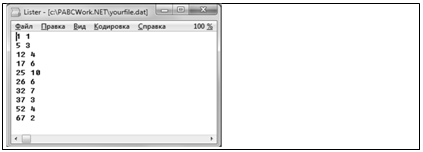
Алгоритмы нахождения оценок параметров и прогнозирования показателей надежности ПО Для оценки l применим метод размножения выборок, известный как метод бутстреппинга [3]. Исходной информацией является выборка наблюдаемых значений (массив данных), в данном случае содержащая три показателя (см. табл.).
Таким образом, при методе бутстреппинга, имея некоторую выборку конечной размерности n, то есть эмпирическое распределение, и используя датчики случайных чисел, из нее можно сформировать любое количество размноженных выборок. Здесь вероятностное распределение в формируемых выборках должно подчиняться пуассоновскому распределению. Рассмотрим алгоритм формирования случайных чисел, распределенных по закону Пуассона. Алгоритм 1. Формирование бутстреп-выборок. Входные параметры: массив наблюдаемых значений M={m1, m2, …, mi, mn} количества ошибок за время исполнения программы; t=0 – текущее время; T – общее время моделирования; I=0 – количество событий за время моделирования T; l – интенсивность ошибок; j – текущий элемент массива; n – размерность выборки. 1. Пока j£n. 2. Генерация случайного числа с равномерным распределением U~U(0, 1) на отрезке (0, 1). 3. 4. Если t>T, то завершить моделирование и выдать результаты. 5. Генерация случайного числа с равномерным распределением U~U(0, 1) на отрезке (0, 1). 6. Если 7. Сформировать строки массива M1={S1(I), m2, …, mj, mn}, поочередно заменяя значение в исходной выборке сгенерированным значением, получая тем самым массивы M2={m1, S2(I), …, mj, mn}, …, Mj={m1, m2, …, Sj(I), mn}, Mm={m1, m2, …, mj, …, Sn(I)}. 8. Конец алгоритма. Алгоритм 2. Нахождение оценки m. Входные параметры: начальное значение x0 (формула (19)); TF – общее кумулятивное количество ошибок за все время исполнения программы; массив времени исполнения программы T – второй столбец из таблицы; массив сформированных размноженных выборок M из алгоритма 1; n – размерность массивов T и M; eps – точность; time – общее время исполнения программ. 1. 2. Повторять 2.1. 2.2. Цикл от 1 до n (расчеты по формуле (20)): 2.2.1. 2.2.2. 2.2.3. 2.2.4. 2.2.5. Конец цикла по n; 2.3. Если t4<0,01, тогда t4=0,01; 2.4. 2.5. 2.6. t4=0; 2.7. 2.8. Конец цикла. Повторять, пока ½MuNew–Mu½£eps. 3. Результат. Вывод Mu. 4. Конец алгоритма. Опишем общую процедуру прогнозирования ожидаемого количества ошибок, которые могут проявиться при дальнейшем исполнении программ на интервале времени t, следующем за кумулятивным интервалом наблюдения tI. В соответствии с рассматриваемым неоднородным пуассоновским процессом среднее ожидаемое количество ошибок
Оценка параметров по предложенным алгоритмам 1 и 2 позволяет записать выражение (21) с использованием оцененных параметров
Шаги процедуры следующие. 1. Получить оценки 2. Отсортировать по возрастанию полученные оценки средней интенсивности ошибок 3. Определить требуемые доверительные интервалы (обычно нижнее значение a=0,05, а верхнее значение a=0,95) и отсечь не входящие в эти интервалы оценки. 4. Используя оценку среднего значения и известные свойства функции распределения Пуассона, можно ожидать, что на интервале времени tI, tI+t количество ошибок будет не более Реализация ПО Предложенный в статье метод прогнозирования был реализован в виде программы, написанной на языке Паскаль в свободной среде программирования PascalABC.NET [4]. Программа включает следующие функции: FirstValue – определение начального значения x0 (по выражению (19)); FindMu – определение оценки m (по алгоритму 2); GenerateLambdas – определение оценки l по методу размножения выборок (алгоритм 1); AssignPoissons – нахождение случайных чисел по распределению Пуассона (элемент алгоритма 1). Исходные данные читаются из файла, имеющего табличную структуру (см. рис.). Первый столбец содержит кумулятивное время исполнения программы (например в днях), а второй – количество ошибок, зафиксированных в определенные временные интервалы (например, через 5 дней были обнаружены и исправлены 3 ошибки в ПО). При запуске программы с данным тестовым файлом можно увидеть результаты, например, прогноза проявления ошибок в ПО с 95 %-ным доверительным интервалом на будущие 10 дней. При необходимости доверительный интервал можно изменить. Подводя итоги, отметим, что в статье предложен метод прогнозирования надежности ПО путем модификации модели, построенной на неоднородном пуассоновском процессе, в котором впервые применен способ размножения выборок, известный как бутстреп-метод. Предложены алгоритмы, позволившие реализовать программу для прогнозирования надежности ПО. Литература 1. Hoang Pham. System Software Reliability. Springer-Verlag Limited. London, 2006, pp. 440. 2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 2007. 504 с. 3. Эфрон Б. Нетрадиционные методы многомерного статистического анализа: сб. статей; [пер. с англ.; предисл. Ю.П. Адлера, Ю.А. Кошевника]. М.: Финансы и статистика, 1988. 263 с. 4. URL: http://pascalabc.net (дата обращения: 20.06.2012). |
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3228 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
| Статья опубликована в выпуске журнала № 3 за 2012 год. [ на стр. 130-134 ] |
Назад, к списку статей



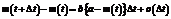 . (2)
. (2) , (3)
, (3)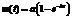 . (4)
. (4) . (5)
. (5)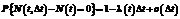 ; (6)
; (6) ; (7)
; (7) , (9)
, (9) , где l(s) – функция интенсивности.
, где l(s) – функция интенсивности. .
. (10)
(10) , (11)
, (11)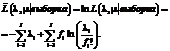 (12)
(12) (13)
(13) . (14)
. (14)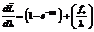 ,
, . (15)
. (15) из выражения (15) в выражение (13), взяв производную по переменной m и приравняв ее к нулю, получаем
из выражения (15) в выражение (13), взяв производную по переменной m и приравняв ее к нулю, получаем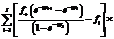
 (16)
(16) ; (17)
; (17) . (18)
. (18)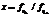 , (19)
, (19) . (20)
. (20)

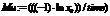 .
. ;
;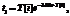
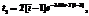

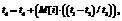

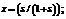

 (21)
(21)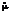 :
:
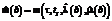 , где b=1, 2, …, B, размноженные методом бутстреппинга-выборки (всего B оценок средней интенсивности ошибок).
, где b=1, 2, …, B, размноженные методом бутстреппинга-выборки (всего B оценок средней интенсивности ошибок). .
. .
.