Авторитетность издания
Добавить в закладки
Следующий номер на сайте
Алгоритм поиска ближайших соседей
Аннотация:Дается описание оригинального алгоритма поиска ближайших соседей среди множества частиц в евклидовом пространстве. Принцип работы алгоритма заключается в представлении множества частиц в виде структуры данных линейного списка, в котором ближайшие соседи находятся рядом в порядке следования номеров элементов, так что поиск очередной пары соседей осуществляется путем сопоставления очередной точки со следующими (по порядковому номеру) элементами списка. Алгоритм позволяет решить задачу поиска всех соседей среди N частиц за время O(N2k), где k2 – коэффициент концентрации частиц. В статье приводятся экспериментальные зависимости изменения значений показателя k от плотности распределения частиц в двумерном пространстве, в которых отмечается изменение значения этого показателя до 20 единиц. В описанных экспериментах алгоритм показывает наибольшую эффективность для случая с высокой концентрацией частиц: при концентрации 80 % для поиска очередной пары со-седей ему потребуется в среднем 1,3 операции, при концентрации 40 % – 1,5 операции, 2,5 операции при 20 %-ной концентрации и от 3 до 4,5 операций при концентрации от 10 до 5 % соответственно. Алгоритм эффективно реали-зуется средствами программирования, что делает его привлекательным для использования.
Abstract:The article describes special algorithm for nearest neighbor search in the set of particles in Euclidean space. The algorithm presents the set of particles in the form of linear list data structure; in this list nearest neighbors are placed close to each other, according to sequence numbering of such elements, so, next search of neighboring pair is made through comparison of the next point with following points (according to sequence number) in the list of elements. The algorithm provides search of all neighbors among N particles in O(N2 k) time, where k2 – density coefficient of particle distribution. The article gives experimental dependencies of coefficient k vs. particle distribution density in two-dimensional space, where this feature changes up to 20 units. In described experiments the algorithm has highest effectiveness, when the particles have high concentration: when the concentration is 80 %, it shall be needed, average, 1,3 operations in order to find next pair of neighbors; with concentration 40 % – 1,5 operations; with concentration 20 % – 2,5 operations and 3–4,5 operations with concentration 10–5 %, accordingly. The algorithm is effectively implemented with programming software, which makes it attractive for use.
| Автор: Гусев Д.И. (dmitry.gusev@gmail.com) - Владимирский государственный университет | |
| Ключевые слова: метод сглаженных частиц., поиск ближайших соседей |
|
| Keywords: smoothed particle hydrodynamics, nearest neighbors search |
|
| Количество просмотров: 12349 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
При моделировании движения жидкости на основе метода сглаженных частиц [1] наибольшее время на каждом шаге моделирования занимает поиск для каждой частицы всех соседей в радиусе взаимодействия. Известно несколько различных алгоритмов, позволяющих реализовать поиск соседей применительно к этой задаче [2]. Приведем описание оригинального алгоритма, позволяющего решить задачу поиска всех соседей среди N частиц за время O(N2¤k), где k³2 – коэффициент концентрации частиц.
Точки p1 и p2 будут являться соседями, если расстояние между ними не превышает величину радиуса взаимодействия r. Предлагаемый алгоритм позволяет закодировать множество исходных точек в виде линейного списка, в котором частицы находятся рядом (в порядке следования номеров) со своими ближайшими соседями, так что поиск очередной пары соседей будет осуществляться путем сопоставления очередной точки со следующими (по порядку следования номеров) элементами списка. Введем точку p0, находящуюся выше и левее всех моделируемых частиц. Пусть r1 и r2 – расстояния от точек p1 и p2 до точки p0 соответственно. Заметим, что для точек p1 и p2, являющихся ближайшими соседями, будет выполняться неравенство |r1–r2|£r. (1) То есть две соседние точки отдалены от третьей на расстояние, не превышающее радиус взаимодействия r.
Очевидно, что при таком кодировании ближайшие соседи будут находиться на одной и той же или на соседних окружностях. Таким образом, для поиска ближайших соседей достаточно выполнить следующие шаги. Листинг 1. Обобщенный алгоритм поиска ближайших соседей. 1) Упорядочить все множество частиц по возрастанию значений r и a, 2) для i¬1, …, N, 3) для j¬i+1, …, N, 4) если rj–ri£r, 5) тогда (pi, pj) – ближайшие соседи, 6) иначе переход на шаг 3. Упорядочение множества частиц (шаг 1) по значениям r гарантирует, что точки на одной окружности будут находиться в упорядоченном множестве рядом, то есть иметь соседние порядковые номера, а упорядочение по значению a гарантирует, что эти же точки в пределах одной окружности будут упорядочены снизу вверх по дуге (рис. 2а).
Шаг 3 отвечает за выбор очередной точки pj для сравнения. На шаге 4 алгоритма проверяется выполнение условия (1). Если условие выполняется, значит, найдена очередная пара соседних точек (шаг 5). В противном случае осуществляется переход к следующей точке pi + 1. В результате каждая точка pi будет сравнена с каждой точкой, расположенной выше по дуге на своей окружности, и со всеми точками последующих окружностей, для которых выполняется условие (1). Так, на рисунке 2а точка 1 сравнивается с точками 2–9, а точка 5 – с точками 6–12. Для точки 5 можно заметить, что точки 6 и 10 находятся за пределами радиуса взаимодействия (рис. 2б). По этой же причине для точки 10 точка 12 не будет соседней, хотя они находятся на одной окружности. Чтобы исключить заведомо ложные сравнения, помимо условия (1), нужно учитывать и угол a каждой точки. В общем случае для точки pi точка pj будет соседней, если выполнится условие ajÎ(ai±Da), (2) где угол Da вычисляется по теореме косинусов из треугольника ABC (рис. 3): Da=arccos((rj2+ri2–r2) ¤ (2×rj×ri)). С учетом условия (2) предлагаемый алгоритм выглядит следующим образом. Листинг 2. Поиск соседей с учетом углов. 1) Упорядочить все множество частиц по возрастанию значений r и a, 2) построить индекс начальных позиций для всех точек одного радиуса, 3) для i¬1, …, N, 4) для j¬i+1, …, N, 5) рассчитать значение Da, 6) если ajÏ(ai±Da), 7) тогда j¬ найти индекс следующей соседней точки, 8) если точка найдена на одном из ближайших радиусов, 9) тогда переход на шаг 11 с новым значением j, 10) иначе переход на шаг 3, 11) если rj–ri£r, 12) тогда (pi, pj) – ближайшие соседи, 13) иначе переход на шаг 3. Здесь на шаге 7 запускается процедура поиска порядкового номера точки с углом aj, удовлетворяющим условию (2), на окружности следующего радиуса. Чтобы реализовать этот шаг, на шаге 2 строится индекс, ключом которого является ра- диус точки, а значением – номер позиции на упорядоченном множестве точек, где встречается первая точка с этим радиусом. Таких данных достаточно, чтобы на упорядоченном подмножестве точек реализовать поиск искомой точки, используя эффективный алгоритм бинарного поиска. Переход к трехмерной системе координат предполагает представление положения каждой точки через два угла и расстояние r. То есть к углу a, лежащему на плоскости XY, добавляется угол b, лежащий на плоскости YZ. В этом случае упорядочение нужно производить по значениям r, a и b, а далее дополнительно выполнять шаги 5–10 (листинг 2) применительно к углу b.
Использование округленных значений может привести к незначительному изменению последовательности шагов в листинге 2. Так, при расчете Da могут возникнуть ситуации, когда не выполнится условие существования треугольника ABC (рис. 3). Это приведет к тому, что некоторые пары соседей не будут найдены. Чтобы этого избежать, при вычислении Da нужно искусственно увеличивать значение r на максимальное отклонение округления (на 1 с помощью функции ceil). Расчет Da можно вынести и за пределы цикла, если в качестве rj использовать значение ri. Оценка вычислительной сложности. В предлагаемом алгоритме (листинг 2) выделяются три крупных шага. 1. Упорядочение множества частиц. Так как на каждой итерации алгоритма моделирования жидкости методом сглаженных частиц точки не будут сильно изменять свое положение в пространстве, частицы можно считать частично упорядоченными. При использовании алгоритма быстрой сортировки вычислительная сложность этого шага оценивается как O(N×log N). 2. Построение индекса начальных позиций заключается в последовательном переборе всех частиц и имеет сложность O(N). 3. Перебор всех потенциальных пар частиц-соседей. Сложность этого алгоритма в худшем случае будет O(N2 ¤ 2). Рассмотрим последний шаг подробнее. Худший случай здесь – когда все частицы находятся друг от друга на расстоянии, меньшем r. Однако это маловероятно при моделировании жидкости, так как из-за больших сил отталкивания ее частицы не могут находиться близко друг к другу.
На рисунке 4 показана зависимость а) количества пар соседей и б) количества операций алгоритма от поверхностной концентрации точек в пространстве, которая рассчитывалась как отношение общего количества точек N к площади, занимаемой этими точками. Общее количество соседних точек почти линейно зависит от их концентрации. С увеличением количества соседних точек растет количество операций, которые потребуются алгоритму для поиска всех пар соседей. В качестве области расположения точек брался круг, в котором случайным образом равномерно размещались частицы (с учетом того, что две частицы не могли занимать одно и то же место), N=const=1000, r – радиус взаимодействия точек – принимался равным 5. На рисунке 5 показано, что с ростом концентрации точек среднее количество операций алгоритма, необходимое для поиска одной пары соседей, уменьшается и стремится к единице (это показатель идеального алгоритма, когда на каждом шаге отыскивается одна пара соседей). Проведенные эксперименты показали, что количество операций алгоритма для поиска всех пар соседей можно представить выражением O=N2 ¤ k, где k – коэффициент, зависящий от количества точек и их концентрации. При увеличении числа точек при их постоянной концентрации (увеличивается пространство, занимаемое точками) значение k линейно растет (см. табл.).
В таблице значений коэффициента k=N2/(кол-во операций) в зависимости от поверхностной концентрации и количества частиц. В этом эксперименте частицы распределялись равномерно случайным образом в пространстве, ограниченном квадратом. В каждом столбце количество частиц увеличивается за счет увеличения объема занимаемого пространства (при фиксированной концентрации частиц), а в каждой строке количество частиц изменяется за счет увеличения их концентрации (в фиксированном объеме пространства). Если k представить в линейной форме записи k=a×x+b, то коэффициент a в этом случае будет коэффициентом линейного тренда параметра k. При увеличении концентрации частиц в фиксированном пространстве (количество точек растет) значение коэффициента линейного тренда параметра k изменяется нелинейно, как показано на рисунке 6. Полученные значения коэффициента рассчитывались по уравнению линейной регрессии для каждого столбца таблицы. В результате сложность алгоритма является аддитивной по отношению к трем перечисленным выше шагам и зависит от положения частиц в пространстве. Перебор всех потенциальных частиц соседей является самым сложным шагом, поэтому вычислительная сложность алгоритма определяется по нему. Простота используемых структур данных и вспомогательных процедур, используемых в предлагаемом алгоритме, а также вычислительная сложность, которая в определенных случаях приближается к идеальной, делают алгоритм привлекательным для применения в задачах моделирования жидкости методом сглаженных частиц. Литература 1. Müller M., Charypar D., Gross M. Particle-Based Fluid Simulation for Interactive Applications Proceedings of ACM SIGGRAPH / EG Symposium on Computer Animation 2003, D. Breen, M. Lin (eds.), (San Diego, CA, USA, July 26–27, 2003). ACM NY, 2003, pp. 154–159. 2. Крюков И.А., Хвостова О.Е., Авербух Е.А. Задача поиска ближайших соседей в рамках моделирования движения жидкости методом сглаженных частиц // Студенческий гений-2010: сб. стат. по матер. VIII Междунар. науч.-практич. конф. студентов, аспирантов и молодых ученых; [под ред. А.И. Аспидова, А.Н. Штефана]. Н. Новгород: Гладкова О.В., 2010. Ч. I. С. 195–202. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постоянный адрес статьи: http://swsys.ru/index.php?page=article&id=3249 |
Версия для печати Выпуск в формате PDF (7.64Мб) Скачать обложку в формате PDF (1.33Мб) |
| Статья опубликована в выпуске журнала № 3 за 2012 год. [ на стр. 231-234 ] |
Назад, к списку статей



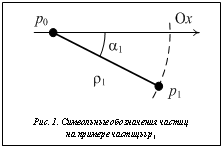 В многомерном пространстве каждая частица p может быть представлена своими координатами. Для простоты иллюстрации, но без ограничения применимости предлагаемого подхода, будем рассматривать частицы в двухмерном евклидовом пространстве. Термин частица в данном контексте заменим термином точка.
В многомерном пространстве каждая частица p может быть представлена своими координатами. Для простоты иллюстрации, но без ограничения применимости предлагаемого подхода, будем рассматривать частицы в двухмерном евклидовом пространстве. Термин частица в данном контексте заменим термином точка. Точку p0 будем рассматривать как центр окружностей с радиусами r1 и r2. Тогда p1 и p2 расположатся на окружностях. Положение каждой точки на окружности определяется углом a, отсчитываемым от оси Ox, на которой лежит точка p0 (рис. 1).
Точку p0 будем рассматривать как центр окружностей с радиусами r1 и r2. Тогда p1 и p2 расположатся на окружностях. Положение каждой точки на окружности определяется углом a, отсчитываемым от оси Ox, на которой лежит точка p0 (рис. 1).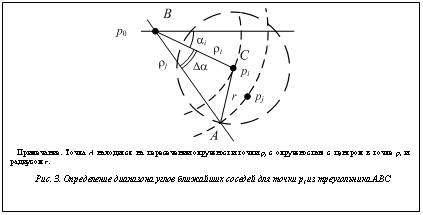 На шаге 2 осуществляется поиск соседей для каждой точки pi. Возможными соседями являются точки, по порядковому номеру следующие за i.
На шаге 2 осуществляется поиск соседей для каждой точки pi. Возможными соседями являются точки, по порядковому номеру следующие за i.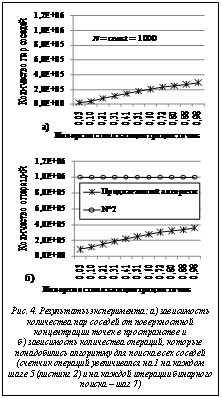 Особенности программной реализации алгоритма. В алгоритме используется большое число операций с плавающей точкой. При реализации некоторых шагов, например 1, 2, 7 и 11 (листинг 2), удобнее оперировать округленными (функцией ceil) значениями радиусов r.
Особенности программной реализации алгоритма. В алгоритме используется большое число операций с плавающей точкой. При реализации некоторых шагов, например 1, 2, 7 и 11 (листинг 2), удобнее оперировать округленными (функцией ceil) значениями радиусов r.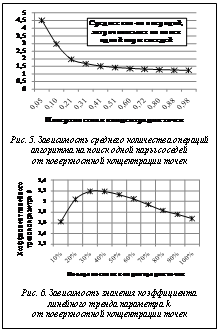 В общем случае количество операций алгоритма зависит не только от количества точек N, но, что важнее, от количества соседей, а количество соседей – от положения точек в пространстве.
В общем случае количество операций алгоритма зависит не только от количества точек N, но, что важнее, от количества соседей, а количество соседей – от положения точек в пространстве.